
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение Максвелла.Средняя, среднеквадратичная и наивероятная скорости молекул.Содержание книги
Поиск на нашем сайте Предполагаем, что состояние газа равновесное, рассм. распределение молекул газа по скоростям. Введем воображаемое пр-во скоростей в котором каждой отдельной молекуле в ПДСК будут соответствовать ск-ти
Во сколько раз увеличивается число молекул газа в объеме, во столько же раз возрастает плотность М.точек, а плотность М.точек пропорциональна числу молекул N. Nогда плотность М.точек можно представить в виде функции Nf(v). Зная вид ф-ции f(v) можно найти число молекул Если взять объем прямоуг. параллелепипеда со сторонами Если в соответствии с нашим рисунком рассматривать шаровой слой радиусом V и толщиной dv, то молекулы, находящиеся в этом слое, обладают скоростями, модули которых лежат в интервале от V до V+dv. Чтобы найти число Где
Коэф. пропорциональности А определяется из условия Соответствующий расчет для коэффициента А дает ее значение Тогда окончательное выр. для ф-и распределения молекул газа по скоростям запис. в виде:
Эта ф-я наз. ф-ей распределения Максвелла. В этой формуле под знаком Наиболее вероятной скоростью, которой обладает молекула газа Продиф-вав это ур-ние Значение, кот. соответствует max-муму наиверостной ск-ти, опред-ся из равенства Из формул для ф-и распределения вероятности для средней арифметической ск-ти мы можем записать Тогда средняя квадратичная ск-ть
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |

 ,
,  ,
,  , т.е. в этом пространстве каждой молекуле будет соответствовать точка, наз-емая молекулярной точкой(М.точкой).
, т.е. в этом пространстве каждой молекуле будет соответствовать точка, наз-емая молекулярной точкой(М.точкой). В равновесном состоянии молекулы газа движутся хаотично и все направленные движения молекул равноправны и положение м.точек относительно начала координат сферически симметрично. В этом случае плотность М.точек, т.е. число их в единице объема V пр-ва явл-ся ф-ей расстояния от начала координат, т.е. ф-ей модуля ск-ти.
В равновесном состоянии молекулы газа движутся хаотично и все направленные движения молекул равноправны и положение м.точек относительно начала координат сферически симметрично. В этом случае плотность М.точек, т.е. число их в единице объема V пр-ва явл-ся ф-ей расстояния от начала координат, т.е. ф-ей модуля ск-ти. , компоненты скорости которых заключены в пределах интервалов
, компоненты скорости которых заключены в пределах интервалов  ,
,  ,
,  , лежащих в окрестности геом. точки с координатами
, лежащих в окрестности геом. точки с координатами  ,
,  таких молекул, нужно умножить плотность М.точек, соответствующих данному значению, на объем шарового слоя, равный
таких молекул, нужно умножить плотность М.точек, соответствующих данному значению, на объем шарового слоя, равный  , т.е.
, т.е.  , где f(v) – функция распределения вероятности значений скорости V. Эту ф-ю теоретически получил Максвелл и она имеет вид
, где f(v) – функция распределения вероятности значений скорости V. Эту ф-ю теоретически получил Максвелл и она имеет вид 
 - масса молекулы
- масса молекулы - постоянная Больцмана
- постоянная Больцмана - абсолютная температура
- абсолютная температура , кот. наз. условием нормировки ф-и
, кот. наз. условием нормировки ф-и  .
. .
.
 стоит выр.
стоит выр.  т.е. отношение кинетич. эн. молекулы для данной скорости
т.е. отношение кинетич. эн. молекулы для данной скорости  к величине КТ, хар-ющей среднее значение тепловой энергии молекул.
к величине КТ, хар-ющей среднее значение тепловой энергии молекул.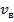 , будет скорость, отвечающая max-муму ф-и
, будет скорость, отвечающая max-муму ф-и 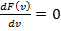 . Исключив из нее коэф-ты, не зависящие от скорости v:
. Исключив из нее коэф-ты, не зависящие от скорости v:  .
. .
. ;
; 
 , где
, где 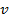 - значение ск-ти при данной температуре T.
- значение ск-ти при данной температуре T. и значение ее
и значение ее  .
.


