
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типы волн и их характеристики. Плоская синусоидальная волнаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Волна называется плоской, если ее волновые поверхности представляют сов-ть плоскостей, || друг другу. В плоской волне, распространяющейся вдоль оси Ох, все величины S, хар-щие колебат. движ. среды, зависят только от времени t и координаты x, рассматриваемой т.М среды. Если в среде нет затухания, то колебания в т.М отличаются от колеб. в нач. коорд. x=0 только тем, что они сдвинуты по времени на величину Ур-ние плоской синусоид. волны, распространяющейся в непоглощающей среде, вдоль положит. направления Ох, имеет вид: Величина Расстояние Длина волны = расстоянию между двумя ближайшими точками среды, в кот. разность фаз. колеб. =
Сферическая и стоячие волны Волна наз. сферич., если ее волновые пов-ти имеют вид концентрических сфер. Центр этих сфер наз. центром волны. Ур-ние расходящ. сферич. волны имеет вид Ур-ние синусоид. сферич. волны: Распространение плоской и расходящейся сферических волн в однородной изотропной среде описывается ДУ частных производных, кот. наз. волновым ур-нием Скорость Для плоской синусоид. волны мы имеем выражение для фазы Продиф-ем это выр. один раз по t и по x.
Для сферич. синусоид. волны может записать для ск-ти Стоячей волной наз. волна, образующаяся в рез-те наложения 2-х бегущих синусоид. волн, распространяющихся навстречу друг другу и имеющих одинаковые частоты и амплитуды. Ур-ние стоячей волны имеет вид: Из этого ур-ния видно, что амплитуда стоячей волны =:
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 592; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.178.7 (0.009 с.) |

 , где
, где 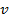 - ск-ть волны, поэтому в плоской волне, распространяющейся вдоль положит. направления оси Ох, S явл. ф-ей разности
- ск-ть волны, поэтому в плоской волне, распространяющейся вдоль положит. направления оси Ох, S явл. ф-ей разности  и ур-ние такой плоской волны имеет вид
и ур-ние такой плоской волны имеет вид 
 или
или 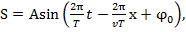 где A – амплитуда колеб., амплитуда волны;
где A – амплитуда колеб., амплитуда волны;  - циклич. или круговая частота волны;
- циклич. или круговая частота волны;  - период колеб.;
- период колеб.;  - нач. фаза колеб. в мом. времени t=0 в точке коорд. плоскости x=0.
- нач. фаза колеб. в мом. времени t=0 в точке коорд. плоскости x=0. , равная фазе колеб. в произвольной точке с коорд. x, наз. фазой плоской сферич. волны.
, равная фазе колеб. в произвольной точке с коорд. x, наз. фазой плоской сферич. волны. , на кот. распространяется синусоид. волна за время, = периоду колеб., наз. длиной волны.
, на кот. распространяется синусоид. волна за время, = периоду колеб., наз. длиной волны. . Тогда ур-ние плоской синусоид. волны можно представить в виде:
. Тогда ур-ние плоской синусоид. волны можно представить в виде: , где
, где  наз. волновым числом и фаза плоской синусоид. волны
наз. волновым числом и фаза плоской синусоид. волны  .
. , где
, где  – расстояние от центра волны до рассматриваемой т.М среды;
– расстояние от центра волны до рассматриваемой т.М среды;  , где
, где  – амплитуда волны;
– амплитуда волны;  - физ. величина, численно равная амплитуде волны на единичном расстоянии от ее центра;
- физ. величина, численно равная амплитуде волны на единичном расстоянии от ее центра;  - нач. фаза колебаний в центре волны.
- нач. фаза колебаний в центре волны. или
или  , где
, где 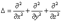 и наз. оператором Лапласа скалярного поля.;
и наз. оператором Лапласа скалярного поля.;  – физ. величина, кот. хар-ет возмущение, распространяющееся в среде со скоростью
– физ. величина, кот. хар-ет возмущение, распространяющееся в среде со скоростью  .
. т.к.
т.к. 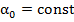 .
. 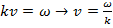 , т.е. фазовая ск-ть связана с циклич. частотой и волновым числом.
, т.е. фазовая ск-ть связана с циклич. частотой и волновым числом. .
.
 . Точки, где
. Точки, где  , наз. узлами, а где
, наз. узлами, а где  – пучностями стоячей волны.
– пучностями стоячей волны.


