
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параллельность прямой и плоскостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
№11 ( устно ). Дан куб АВСDA1B1C1D1 (рис. 24). 1. Докажите, что а) DC параллельно плоскости грани АА1В1В; б) АС параллельно плоскости А1C1D; в) А1D параллельно плоскости грани ВВ1C1С. 2. Назовите все рёбра куба, параллельные плоскости основания. 3. Каким граням куба параллельно ребро АD? 4. М – середина ребра AD, N – середина ребра DC. Докажите, что MN параллельно плоскости диагонального сечения АА1С1С. Назовите все плоскости, проходящие через вершины куба, параллельные MN.
№12 ( устно ). Средняя линия трапеции лежит в плоскости α. Пересекают ли прямые, содержащие основания трапеции, плоскость α? Ответ обосновать.
Рис. 25 №13. Параллельна ли плоскость АSС прямой, проходящей через точки Р и Р1 пересечения медиан треугольников SАВ и SСВ (рис. 26)? Ответ обосновать.
План решения. 1. Δ PBР1~ Δ MBM1. 2. РР1 || ММ1. 3. Вывод.
№14 ( устно ). Известно, что прямая параллельна плоскости. Параллельна ли она любой прямой в этой плоскости? Может ли данная прямая пересечь хотя бы одну из прямых плоскости? №15 ( устно ). Будут ли параллельны две прямые, параллельные одной и той же плоскости? №16. Плоскости α и β пересекаются по прямой с (рис. 27). Прямая р параллельна каждой из этих плоскостей. Докажите, что она параллельна прямой с.
1. Существует прямая 2. а¢ || β. 3. а¢ || с. 4. р || с.
№17. Отрезки АА1, ВВ1, СС1 не лежат в одной плоскости и пересекаются в точке О, являющейся серединой каждого из них. Доказать, что прямая АВ параллельна плоскости А1СВ1.
1. Δ АОВ= Δ А1ОВ1. 2. АВ || А1В1. 3. А1В1Ì А1СВ1. 3. Вывод.
№18. Объясните, почему кóзлы, на которых пилят брёвна обеспечивают горизонтальное положение бревна. № 19. В кубе АВСDA1B1C1D1 точка К1 – середина ребра АВ, точка К2 – середина ребра АА1, точка К3 – середина ребра А1В1, точка К4 – середина ребра СС1, точка К5 – середина ребра СD. Как расположены между собой такие прямые и плоскости: а) К2 К3 и К1К4К5;
1. К2 К3 || К5 К4. 2. Вывод.
Ответ: К2 К3 || К1К4К5.
б) К1К4 и AB1D;
Пусть точка О – середина АВ1. 1. ОС1 – линия пересечения сечения АВ1С1D и К1К3С1С. 2. К1К4 || ОС1, 3. Вывод. Ответ: К1К4 || AB1D.
План решения. 1. К3D || В1К5. 2. К3D пересекает плоскость К2К3К4.
3. Вывод. Ответ: В1К5 пересекает плоскость К2К3К4.
План решения. 1.Точка О (середина отрезка К3К5) – центр симметрии куба. 2. MN || ВD, 3. MN пересекает плоскость К2К3К5. 4. Вывод. Ответ: BD пересекает плоскость К2К3К5
№ 20. В правильной четырёхугольной пирамиде провести плоскость через диагональ основания параллельно боковому ребру. Сторона основания равна а, а боковое ребро равно в. Определить площадь полученного сечения.
План построения. План вычисления площади. 1. ОК || PD в плоскости BPD (рис. 33) 1. АС. 2. АК, КС. 2. Δ АКС – равнобедренный. 3. Δ АКС – искомое сечение. 3. ОК – высота Δ АКС. 4. Δ BPD ~ Δ BKO, k =2. 5. OK. 6.S Δ ABC. Ответ: № 21. Построить сечение тетраэдра DABC плоскостью, параллельной прямой AD, проходящей через вершину С и внутреннюю точку М ребра АВ. Найти площадь сечения, если каждое ребро тетраэдра имеет длину а и точка М делит ребро АВ пополам.
План построения. План вычисления. 1. MN || AD. 2. NC. 3.CM. 1. Вид сечения MNC. 4. MNC – искомое сечение. 2. NM. 3. МС. 4. РС. 5. SΔNMC. Ответ: № 22. В правильной треугольной пирамиде SABC с вершиной S проведена плоскость, которая параллельна медиане основания BN и пересекает боковые ребра SA в точке К, а SB в точке L, причём SK=
1. Сечение BSN. 2. LT || BN (рис. 36). 3.KT. 4. Точка Р – пересечение КТ и SC. 5. PL. 6. LK. 7. Δ LPK – искомое сечение.
Рассмотреть грань пирамиды АSC. Провести AR || KP, NQ || KP (рис. 37). 1. ST = 2. ST=TF=FN. 3. SP=PR=RQ. 4. RQ=QC. 5. SP=PR=RQ=QC. 6. SP: PC=1: 3.
Ответ: 1: 3.
№ 23. В правильной четырёхугольной пирамиде SABCD точка М принадлежит ребру SD. Построить сечение пирамиды плоскостью, проходящей через точки В, М и параллельной прямой АС.
План построения. 1. МВ (рис. 38). 2. О – точка пересечения SQ и МВ. 3. KF: OÎ KF и KF || AC (рис.39). 4. Сечение KMFB (рис.40).
№ 24. Пусть АВСA1B1C1 – правильная призма. Точка К – середина ребра АС. 1) Отметить точку L на ребре В1С1, такую, чтобы отрезок KL был параллелен грани АА1В1В. 2) Как вычислить длину LK, если рёбра призмы известны?
План построения. План вычисления. 1. Точка F – середина АВ. 1. КМ. 2. KL.
2. FB1. 3. Прямая р: р || FB1 и КÎ FB1. 4. L – точка пересечения прямой р и B1C1.
№ 25 ( устно ). В правильной призме АВСА1В1С1 точка К – середина ребра ВВ1. Провести сечение призмы плоскостью, проходящей через точку К параллельно АС. Какое из них: а) параллельно В1С; б) параллельно А1В; в) имеет наибольшую площадь; г) имеет наименьшую площадь?
№ 26 (устно). Верно ли утверждение, что если плоскости α и β параллельны и прямая а лежит в плоскости α, то эта прямая параллельна плоскости β (рис. 47).
№ 28 (устно). Если две параллельные прямые одной плоскости параллельны двум прямым другой плоскости, то будут ли эти плоскости параллельны?
№ 29 (устно). Верно ли утверждение: если две прямые, лежащие в одной плоскости, параллельны другой плоскости, то эти плоскости параллельны?
№ 30 (устно). Основание призмы - трапеция. Доказать, что призма имеет только одну пару параллельных боковых граней.
№ 32 (устно). Две стороны треугольника параллельны плоскости α. Доказать, что и третья его сторона параллельна плоскости α.
План доказательства. 1. DA1OB1=DA2OB2. 2. A1B1|| A2B2. 3. DA1OC1=DA2OC2. 4. A1C1|| A2C2. 5. Вывод. В задачах №34- №35 выбираются два отрезка, лежащие на скрещивающихся прямых. № 34. Дана правильная треугольная пирамида. Построить два её параллельных сечения, проходящих через:
План построения. MN, РQ – средние линии 1. МК || AD. 2. КN. 3. Плоскости MKN и ADC параллельны.
2) апофему и среднюю линию боковой грани;
MN – средняя линия грани ADC, DQ – апофема. 1. NP || DQ. 2. PM. 3. QC ||PM. 4. Плоскости PNM и QDC параллельны.
План построения. MN – средняя линия грани AВC, DР –медиана боковой грани ADC. 1. ВDP. 2. Q – точка пересечения MN и BP. 3. QK || DP. 4. MKN.
4) медианы двух боковых граней;
План построения. DM –медиана боковой грани ADC, АК – медиана боковой грани AВD 1. BDM. 2. KP || DM. 3. AP. 4. Q – точка пересечения АР и ВС. 5. QK. 6. MN || AQ. 7. DN. 8. Плоскости КАQ и DMN параллельны.
5) высоту пирамиды и среднюю линию боковой грани;
План построения. MN – средняя линия грани ADC, DО – высота пирамиды. 1. APD. 2. NQ ||DO. 3. MQ. 4. K – точка пересечения 5. KN. 6. DE || NK. 7. EC 8.Плоскости KNM и DEC параллельны.
План построения. DO – высота пирамиды, ВN – медиана боковой грани. 1. DAM. 2. NK || DO. 3. ВК. 4. F – точка пересечения ВК и АС. 5. FN. 6. QP || BF, OÎQP. 7. DQ. 8. Плоскости ВNF и DQP – параллельны. № 35. Пусть АВСDA1B1C1D1 - куб. Построить два его сечения, параллельных между собой и проходящие через:
План построения. 1. А1С1. 2. BD. 3. Плоскости граней ABCD и A1B1C1D1 параллельны.
2) АС и С1D;
План построения. 1. АВ1. 2. В1С. 3. А1С1. 4. А1D. 5. Плоскости АСВ1 и С1DА параллельны.
3) АС и В1D;
1. OK ||B1D. 2. AK. 3. KC. 4. MN || AC. 5. Q – точка пересечения MN и В1D. 6. MB1. 7. B1N. 8. ND. 9. DM. 10.Плоскости треугольника АКС и четырёхугольника MB1ND параллельны.
АА1В1В и А1В1С1D1. План построения. 1.А1С1. 2. А1В. 3. С1В. 4. АС. 5. АD1. 6. CD1. 7. Плоскости А1С1В и АСD1 параллельны. № 36. В правильном тетраэдре с ребром а DO – высота тетраэдра. Точка М – середина DO. 1) Провести через точку М сечение, параллельное плоскости ACD. 2) Вычислить периметр и площадь сечения.
План построения. 1. P – точка пересечения ВО и АС. 2. Плоскость BDP. 3. RQ || DP, MÎRQ. 4. KN || AC, QÎ KN. 5. RK. 6. RN. 7. Сечение KRN параллельно грани ADC. 2) 1. D KRN ~ D ADC. 2. Коэффициент подобия k= RQ: DP. 3. РDАDC. 4. РDKRN. 5. S DАDC. 6. SDKRN. Ответ:
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 2237; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.112.183 (0.012 с.) |


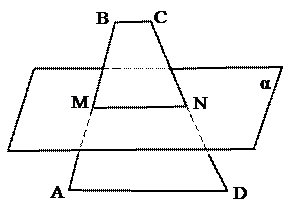


 План доказательства.
План доказательства.
 План решения.
План решения. План решения.
План решения.
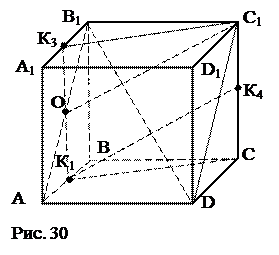 План решения.
План решения.
 в) В1К5 и К2К3К4;
в) В1К5 и К2К3К4; г) BD и К2К3К5;
г) BD и К2К3К5;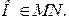



 .
.


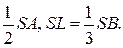 Вычислить, в каком отношении плоскость сечения делит ребро SC?
Вычислить, в каком отношении плоскость сечения делит ребро SC? План построения.
План построения. План вычисления.
План вычисления.



 1) 2)
1) 2)





 3.3.Параллельность плоскостей
3.3.Параллельность плоскостей
 № 27 (устно). Доказать, что 1) противоположные грани параллелепипеда параллельны; 2) сечения параллелепипеда, проходящие через тройки его вершин А, В1, С и А1, С1, D, параллельны между собой. Сколько пар таких сечений можно провести?
№ 27 (устно). Доказать, что 1) противоположные грани параллелепипеда параллельны; 2) сечения параллелепипеда, проходящие через тройки его вершин А, В1, С и А1, С1, D, параллельны между собой. Сколько пар таких сечений можно провести?



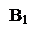










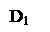










 № 31 (устно). Дан тетраэдр DABC. Точки М, N, P являются серединами ребер DA, DB, DC. Доказать, что плоскости MNP и ABC параллельны.
№ 31 (устно). Дан тетраэдр DABC. Точки М, N, P являются серединами ребер DA, DB, DC. Доказать, что плоскости MNP и ABC параллельны.
 № 33. Три отрезка А1А2, В1В2 и С1С2, не лежащие в одной плоскости, имеют общую середину. Доказать, что плоскости А1В1С1 и А2В2С2 параллельны.
№ 33. Три отрезка А1А2, В1В2 и С1С2, не лежащие в одной плоскости, имеют общую середину. Доказать, что плоскости А1В1С1 и А2В2С2 параллельны. 1) среднюю линию основания и среднюю линию боковой грани;
1) среднюю линию основания и среднюю линию боковой грани; План построения.
План построения. 3) среднюю линию основания и медиану боковой грани;
3) среднюю линию основания и медиану боковой грани; 5.Плоскости MKN и ADC параллельны.
5.Плоскости MKN и ADC параллельны.

 6) высоту пирамиды и медиану боковой грани.
6) высоту пирамиды и медиану боковой грани. 1) АС и В1D1;
1) АС и В1D1;
 План построения.
План построения. 4) АС и О1О2, где О1 и О2 – центры граней
4) АС и О1О2, где О1 и О2 – центры граней




