
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Признак параллельности прямыхСодержание книги
Поиск на нашем сайте Две прямые, параллельные третьей, параллельны между собой [5, с.11], [10, с.13].
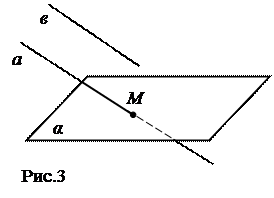
Свойство параллельных прямых Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость [5, c. 10].
a || b, а пересекает плоскость α в точке М: прямая в пересекает плоскость α.
Параллельность прямой и плоскости Определения 1. Прямая и плоскость называются параллельными, если они не имеют общих точек [5, с.11]. 2. Прямая и плоскость называются параллельными, если они не пересекаются, то есть не имеют общих точек [10, с.14].
Признак параллельности прямой и плоскости Если прямая, не лежащая в плоскости, параллельна какой-нибудь прямой, лежащей в плоскости, то она параллельна самой плоскости [5, с.12], [ 10, c.13].
Существует прямая в такая, что в Ì α и в || a: a || α.
Параллельность плоскостей Определение. Две плоскости называются параллельными, если они не пересекаются, то есть не имеют общих точек. [5, с.20], [ 10, с.15].
Признак параллельности плоскостей
Дополнительные признаки параллельности прямых
2. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны [5, с.21], [10, с.17].
Доказательства утверждений теоретической карты №1 Параллельность прямых Доказательство признака параллельности прямых приводится в учебниках [5, с.11], [10, с.13]. Доказательство свойства параллельных прямых приводится в учебнике [5, с.10]. Параллельность прямой и плоскости Доказательство признака параллельности прямой и плоскости приводится в учебниках [5, с.12], [10, с.14]. Параллельность плоскостей Доказательство признака параллельности плоскостей приводится в учебниках [5, с.20, 21], [10, с.15]. Дополнительные признаки параллельности прямых Доказательство первого дополнительного признака параллельности прямых приведено в учебнике [5, с.12]. Доказательство второго дополнительного признака параллельности прямых приводится в учебниках [5, с.35], [10, с.17]. Задачи к теоретической карте №1 Параллельность прямых
№ 2 ( устно ). Дан параллелепипед. Доказать, что: а) для каждого его ребра в нём найдутся три ребра, ему параллельные (рис.13); б) для каждой диагонали его грани найдётся ей параллельная и равная диагональ в другой грани (рис. 14).
№ 3. Прямая в лежит в плоскости α и параллельна прямой а, не лежащей в этой плоскости. Через точку М плоскости α
План доказательства.
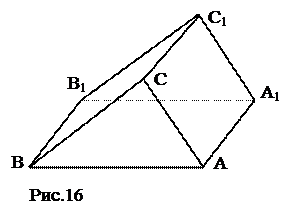
№ 4. Даны два параллелограмма АВВ1А1 и АСС1А1 (рис. 16). Доказать, что Δ АВС = Δ А1В1С1.
План решения. 1. ВВ1С1С – параллелограмм. 2. Δ АВС= Δ А1В1С1.
№ 5. Точка М находится вне плоскости параллелограмма ABCD. Найдутся ли параллельные средние линии у треугольников: а) МАВ и МАD;
План решения. а) 1. Р1- середина ребра DM, Р6- середина ребра DА, Р3- середина ребра MВ, Р5- середина ребра АВ. 2. Р1 Р6 || Р3 Р5.
№ 6. Точка М лежит вне плоскости треугольника АВС. Точки К, Р, Е, F – середины отрезков МА, АВ, МС, ВС. Как расположены прямые КР и ЕF?
1. Провести МВ. 2. КР||МВ, EF||MB. 3. КР|| EF. № 7. На рисунке 20 точки M, H, K, P – середины соответствующих отрезков AD и DC, BC и AB. Найти периметр четырёхугольника MHKP, если МР=8см, АС=32см.
План решения. 1. МНКР – параллелограмм. 2. РК. 3. РМНРК. Ответ: 48 см.
№ 8. Даны четыре точки, A, B, C, D, не лежащие в одной плоскости. Доказать, что прямые, соединяющие середины отрезков AB и CD, AD и BC пересекаются в одной точке.
План решения. 1. Провести АС. 2. Доказать, что NKMF – параллелограмм. 3. О – точка пересечения NM и KF.
№9. ABCDEF – замкнутая пространственная ломанная. Отрезки, соединяющие середины звеньев АВ и EF, ВС и ЕD, равны и параллельны. Параллельны ли звенья CD и AF?
№10. Треугольник ABC и трапеция KMNP имеют общую среднюю линию EF, причём KP || MN, EF || AC. Доказать, что а) АС || KP; б) вычислить KP и MN, если КР:MN=3:5, АС=16 см.
а) EF || KP, EF ||AC. Вывод. б) 1. EF. 2. Выразить КР и MN через переменную. 3. Составить и решить уравнение
Ответ: 6 см, 10 см.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1344; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.008 с.) |






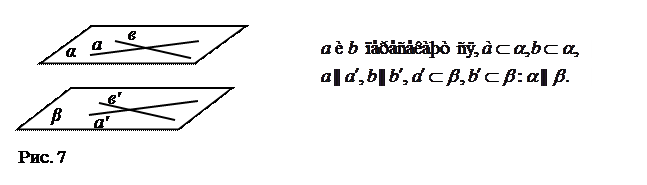 Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны [5, с.20], [10, с.15].
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны [5, с.20], [10, с.15].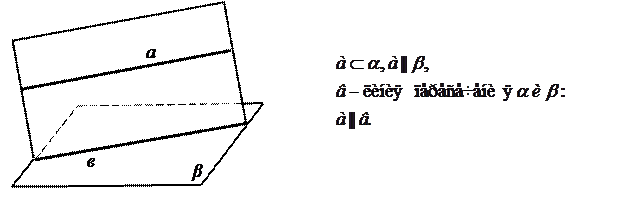



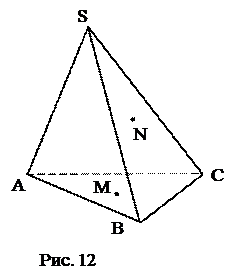 № 1 ( устно ). На боковых гранях призмы отмечены точки М и N. Как через эти две точки провести два параллельных отрезка? Решить аналогичную задачу, заменив призму пирамидой.
№ 1 ( устно ). На боковых гранях призмы отмечены точки М и N. Как через эти две точки провести два параллельных отрезка? Решить аналогичную задачу, заменив призму пирамидой.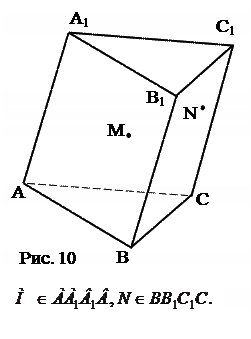



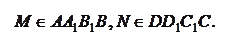
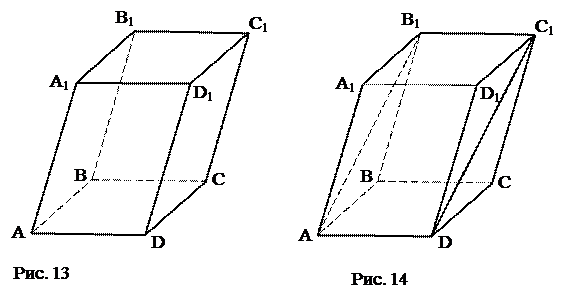
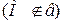 проведена прямая с, параллельная прямой а. Доказать, что прямая с лежит в плоскости α.
проведена прямая с, параллельная прямой а. Доказать, что прямая с лежит в плоскости α.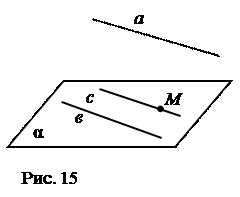
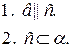
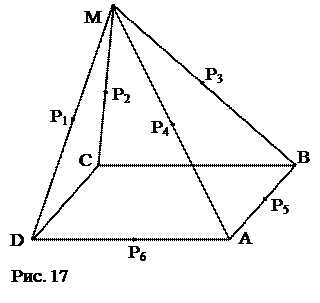 б) МАВ и МСD?
б) МАВ и МСD? б) Аналогично Р1Р2 || Р4Р3.
б) Аналогично Р1Р2 || Р4Р3. План решения.
План решения.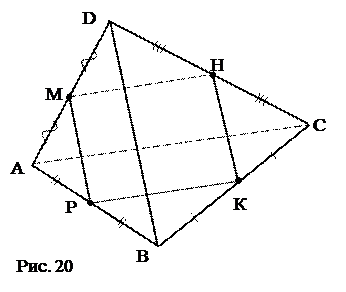
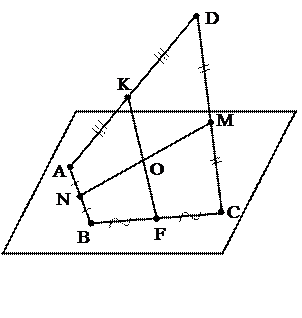

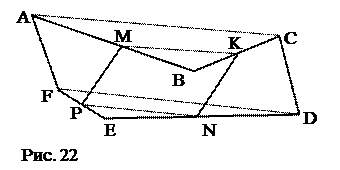 План решения. 1. MKNP – параллелограмм. 2. AC || FD. 3. AC = FD. 4. FACD – параллелограмм. 5. Вывод.
План решения. 1. MKNP – параллелограмм. 2. AC || FD. 3. AC = FD. 4. FACD – параллелограмм. 5. Вывод. План решения.
План решения.



