
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
II. Перпендикулярность в пространствеСодержание книги
Поиск на нашем сайте
ТЕОРЕТИЧЕСКАЯ КАРТА №2 Перпендикулярность прямых Определения
2. Скрещивающиеся прямые называются перпендикулярными, если угол между ними равен 90° [10, c.50]. (Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, которые параллельны данным скрещивающимся прямым [10, c. 50]).
3. Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90°[5, c. 34].
Признаки перпендикулярности прямых 1. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой [5, с. 34].
2. Если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым, то они перпендикулярны [10, с.25].
Перпендикулярность прямой и плоскости Определения 1. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости [10, c.34].
2. Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой, которая лежит в данной плоскости и проходит через точку пересечения [10,с. 26].
Признак перпендикулярности прямой и плоскости 1. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости [5, с. 36], [10, с. 26].
Перпендикулярность плоскостей Определения 1. Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым [10, с. 32].
Признак перпендикулярности плоскостей
Если одна из плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны [5, с.49], [10, с. 33].
Дополнительный признак перпендикулярности прямых
Справедлива и обратная теорема: если прямая, проведённая на плоскости через основание наклонной, перпендикулярна к ней, то она перпендикулярна и к её проекции [5, c. 42], [10, c.31 ]. Обобщённая теорема о трёх перпендикулярах: любая прямая на плоскости, перпендикулярная проекции наклонной на эту плоскость, перпендикулярна и наклонной [10, задача 33, с. 62].
Справедлива и обратная теорема: любая прямая на плоскости, перпендикулярная наклонной к этой плоскости, перпендикулярна и её проекции. Дополнительные признаки перпендикулярности прямой и плоскости 1. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости [5, с. 35], [10, с. 28].
2. Если прямая перпендикулярна к одной из параллельных плоскостей, то она п
3. Если прямая, лежащая в одной из двух перпендикулярных плоскостей, перпендикулярна их линии пересечения, то она перпендикулярна и другой плоскости [10, стр. 41, задача 58].
Дополнительные признаки перпендикулярности плоскостей 1. Плоскость, перпендикулярная к прямой, по которой пересекаются две
2. Если две плоскости параллельны и одна из них перпендикулярна к третьей плоскости, то и вторая перпендикулярна к ней.
Доказательства утверждений теоретической карты №2 Перпендикулярность прямых Доказательство признака перпендикулярности прямых (1) приводится в учебнике Атанасяна [5,с. 34]. Доказательство признака перпендикулярности прямых (2) приводится в учебнике Погорелова [10, с.25] Перпендикулярность прямой и плоскости Доказательство признака перпендикулярности прямой и плоскости приводится в учебниках [5, с. 36], [10, с. 26].
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 3399; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.95.233 (0.005 с.) |

 1. Две прямые называются перпендикулярными, если они пересекаются под прямым углом [10, c. 25].
1. Две прямые называются перпендикулярными, если они пересекаются под прямым углом [10, c. 25].












 2. Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен 90° [5, с.52]. (Определение угла между плоскостями приведено на странице 73).
2. Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен 90° [5, с.52]. (Определение угла между плоскостями приведено на странице 73).
 Теорема о трёх перпендикулярах: если прямая, проведённая на плоскости через основание наклонной, перпендикулярна к её проекции на эту плоскость, то она перпендикулярна и к самой наклонной [5, c. 42], [10, c. 31].
Теорема о трёх перпендикулярах: если прямая, проведённая на плоскости через основание наклонной, перпендикулярна к её проекции на эту плоскость, то она перпендикулярна и к самой наклонной [5, c. 42], [10, c. 31].



 ерпендикулярна и к другой плоскости [5, с.40, задача 132], [8, с. 17].
ерпендикулярна и к другой плоскости [5, с.40, задача 132], [8, с. 17]. 4. Линия пересечения двух плоскостей, перпендикулярных к третьей плоскости, есть перпендикуляр к этой плоскости [8,c. 24].
4. Линия пересечения двух плоскостей, перпендикулярных к третьей плоскости, есть перпендикуляр к этой плоскости [8,c. 24].


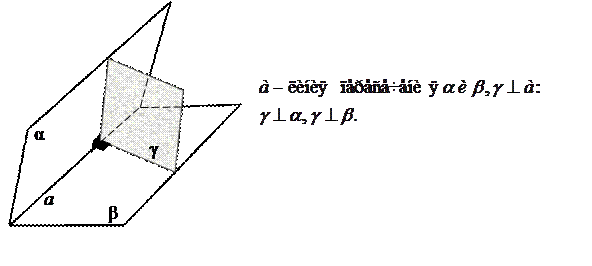 данные плоскости, перпендикулярна к каждой из этих плоскостей [5, с. 49].
данные плоскости, перпендикулярна к каждой из этих плоскостей [5, с. 49].




