
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема косинусов для трёхгранного углаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
№ 62. В трёхгранном угле два плоских угла по 45°,а двугранный угол между ними равен 60°. Найти третий плоский угол. Ответ: № 63. Определить угол между двумя смежными диагональными сечениями в кубе. (Диагональные сечения в кубе называются смежными, если они проходят через смежные стороны основания).
1. Двугранный угол АВ1DС - искомый, пусть его величина j. 2. Рассмотреть трёхгранный угол DAB1C. В обозначениях теоремы о трёх косинусах Ð B1DA=α, ÐB1DC= β, ÐADC=γ,
4. cos j. Ответ: 120°.
№ 64. Линейный угол двугранного угла, составленного двумя смежными боковыми гранями правильной четырёхугольной пирамиды, в два раза больше плоского угла при вершине пирамиды. Найти плоский угол при вершине пирамиды.
1. Построения: DK ^PC, BK. 2. ÐBKD – линейный. 3. Рассмотреть трёхгранный угол CDPB. В обозначениях теоремы о трёх косинусах Ð РСD = α, ÐРCB = β, ÐDCВ = γ, ÐBKD = j. 4. α = β, γ=90°. 5. Выразить α и β через j. 6. Составить уравнение по теореме о трёх косинусах. 7. Решить полученное уравнение относительно cos Ответ:
№ 65. В треугольной пирамиде две боковые грани – равнобедренные прямоугольные треугольники, гипотенузы которых равны с и угол между ними равен γ. Одно из боковых рёбер пирамиды перпендикулярно к плоскости основания. Найти объём пирамиды.
1. Рассмотреть трёхгранный угол PАBC. В обозначениях теоремы о трёх косинусах Ð АРВ=α, ÐCРB=β, ÐАРС=γ, ÐАВС = j. 2. α = β = 45°. 3. cosj (по теореме о трёх косинусах). 4. sinj.
6. S DАВС. 7. VSABC. Ответ: № 66. Отрезок прямой, соединяющий центр основания правильной треугольной пирамиды с серединой бокового ребра, равен стороне основания. Найти косинус угла между смежными боковыми гранями.
1. АО. 2. AS (DASO). 3. cos ÐSAO (DASO). 4.cosÐSAC (по теореме о трёх косинусах). 5. Рассмотреть трёхгранный угол ASBC. В обозначениях теоремы о трёх косинусах двугранный угол с ребром AS равен j, ÐSAC=α, ÐSAB=β, α = β, ÐВАС =γ. 6. ÐВАС. 7. sinÐSAC. 8. cosj (по теореме косинусов). Ответ: № 67. Основанием пирамиды служит правильный треугольник, одна из боковых граней пирамиды перпендикулярна к плоскости основания. Найти косинус угла между двумя другими боковыми гранями, если обе они составляют с плоскостью основания один и тот же угол d.
1. Построения: 1.1. SO ^ ABC. 1.2. OM ^ BC, SM 1.3. OK ^ AC, SK. 2. ÐSKO =ÐSMO = d. 3. Пусть АВ = АС = ВС = а. АО = ОВ=0,5 а. 4. Выразить ОК через а (DАКО). 5. Выразить SК через а (DSКО). 6. Выразить АК через а (DАКО), выразить КС через а (DАКО). 7. tgÐSCK (DSCК), cosÐSCK, sinÐSCK. 8. Рассмотреть трёхгранный угол СASB с вершиной С. В обозначениях теоремы косинусов искомый двугранный угол с ребром SC равен j, ÐSCА=α, Ð SCB=β, α=β, ÐACB=γ. 9. ÐACB=γ. 10. cosj (по теореме косинусов). Ответ: № 68. Стороны основания параллелепипеда равны а и в, а угол между ними равен α. Найти объём параллелепипеда, если боковое ребро, проходящее через вершину данного угла, составляет с его сторонами углы β и γ, а длина его равна с.
1. Построения: А1О ^ ABCD, OK ^ AD, A1K. 2. ÐА1КО – линейный угол двугранного угла с ребром AD. 3. SABCD. 4. А1К.
5. Рассмотреть трёхгранный угол ASBC. В обозначениях теоремы о трёх косинусах двугранный угол с ребром AD равен ÐА1КО = j, ÐBAD= α, ÐА1AD= β, ÐA1АB =γ. 6. cos j (по теореме косинусов). Значение cosj обозначить р. 7. sin j (выразить через р). 8. А1О. 9. Vпризмы. Ответ: № 68. Основанием призмы служит правильный треугольник со стороной, равной а. Боковое ребро равно в и составляет с пересекающими его сторонами основания острые углы, соответственно равные α и β. Найти объём призмы. Решение задачи аналогично решению задачи № 6. Ответ:
СПИСОК ЛИТЕРАТУРЫ 1. Александров А.Д. Геометрия: Учебное пособие для 10-11 кл. общеобразовательных учреждений/ А.Д. Александров, А.Л. Вернер, В.И. Рыжик.- 2-е изд.-М.: Просвещение, 2001.-271с. 2. Александров А.Д. Геометрия для 10-11 кл.: Учебное пособие для учащихся школ и классов с углублённым изучением математики / А.Д. Александров, А.Л. Вернер, В.И. Рыжик. - 3-е изд.-М.: Просвещение, 1992.-464 с. 3. Барыбин К.С. Сборник задач по математике: пособие для учителей 8-10классов/ К.С. Барыбин, А.К. Исаков. – М.: Гос. учеб.- педаг. изд-во Мин. Просвещения РСФСР, 1955. – 207 с.- 4. Габович И.Г. Алгоритмический подход к решению геометрических задач: книга для учителя / И.Г. Габович. – Киев: Радянська школа, 1989. – 160 с. 5. Геометрия: учебник для 10–11 кл. общеобразовательных учреждений / Л.С. Атанасян [и др.]. – М.: Просвещение, 2000. – 206 с. 6. Гусев В.А. Практикум по решению математических задач: Геометрия: учебное пособие для студентов физ.-мат. спец. пед. ин-тов / В.А. Гусев, В.Н. Литвиненко, А.Г. Мордкович. – М.: Просвещение, 1985. – 223 с. 7. Зив Б.Г. Задачи по геометрии: Пособие для учащихся 7 – 11 класса общеобразоват. учреждений/ Б.Г. Зив, В.М. Мейлер, А.Г. Баханский.- 3-е изд.-М.: Просвещение, 2000.-271с. 8. Киселёв А.П. Геометрия: Стереометрия: 10-11 кл.: учебник и задачник / А.П. Киселев, Н.А. Рыбкин. – М.: Дрофа, 1995. – 352 с. 9. Математика. Подготовка к ЕГЭ-2011: учебно-методическое пособие/ Под редакцией Ф.Ф.Лысенко, С.Ю. Кулабухова. - Ростов-на- Дону: Легион -М, 2010 – 416с. 10. Погорелов А.В. Геометрия: учебник для 10 – 11 кл. общеобразоват. учреждений: базовый и профильный уровни / А.В. Погорелов. – 10-е изд. – М.: Просвещение, 2010. – 175 с. 11. Сборник конкурсных задач по математике для поступающих во втузы: учебное пособие/Под редакцией М.И. Сканави. - 3-е изд.-М.: Высшая школа, 1977. 12. Смирнова И.М. Геометрия: Учебное пособие для 10-11 кл. естественно- научного профиля обучения / И.М. Смирнова, В.А. Смирнов. – М.: Просвещение, 2001.- 239 с. 13. Смирнова И.М. Устные упражнения по геометрии для 7 – 11 классов:Кн. для учителя / И.М. Смирнова, В.А. Смирнов. – М.: Просвещение, 2003.- 174 с. 14. Худобин А.И. Сборник задач по тригонометрии: пособие для учителей/ А.И. Худобин, Н.И. Худобин. -М.: Гос. учеб.- педаг. изд-во Мин. Просвещения РСФСР, 1954. – 186 с.
СОДЕРЖАНИЕ Предисловие...........................................................................................................3
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1710; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.123.84 (0.017 с.) |


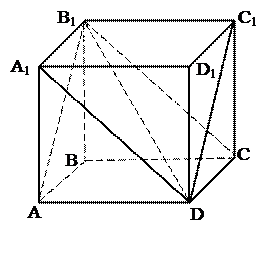 План решения.
План решения. 3. α = β, γ=90°.
3. α = β, γ=90°. План решения.
План решения.

 План решения.
План решения. 5. АВ, АВ=ВС=ВР.
5. АВ, АВ=ВС=ВР.
 План решения.
План решения.
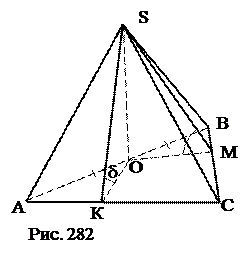 План решения.
План решения.
 План решения.
План решения.





