
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Значение теоремы Чебышева для практикиСодержание книги
Поиск на нашем сайте
Приведем примеры применения теоремы Чебышева крешению практических задач. Обычно для измерения некоторой физической величины производят несколько измерений и их среднее арифметическое принимают в качестве искомого размера. При каких условиях этот способ измерения можно считать правильным? Ответ на этот вопрос дает теорема Чебышева (ее частный случай). Действительно, рассмотрим результаты каждого измерения как случайные величины Х 1, Х 2 ,..., Хп. К этим величинам можно применить теорему Чебышева, если: 1) они попарно независимы, 2) имеют одно и то же математическое ожидание, 3) дисперсии их равномерно ограничены. Первое требование выполняется, если результат каждого измерения не зависит от результатов остальных. Второе требование выполняется, если измерения произведены без систематических (одного знака) ошибок. В этом случае математические ожидания всех случайных величин одинаковы и равны истинному размеру а. Третье требование выполняется, если прибор обеспечивает определенную точность измерений. Хотя при этом результаты отдельных измерений различны, но рассеяние их ограничено. Если все указанные требования выполнены, мы вправе применить к результатам измерений теорему Чебышева: при достаточно большом п вероятность неравенства | (Х 1 + Х 2 +...+ Хп) /n-a|< e как угодно близка к единице. Другими словами, при достаточно большом числе измерений почти достоверно, что их среднее арифметическое как угодно мало отличается от истинного значения измеряемой величины. Итак, теорема Чебышева указывает условия, при которых описанный способ измерения может быть применен. Однако ошибочно думать, что, увеличивая число измерений, можно достичь сколь угодно большой точности. Дело в том, что сам прибор дает показания лишь с точностью ±a; поэтому каждый из результатов измерений, а следовательно, и их среднее арифметическое будут получены лишь с точностью, не превышающей точности прибора. На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят о всей совокупности (генеральной совокупности) исследуемых объектов. Например, о качестве кипы хлопка заключают по небольшому пучку, состоящему из волокон, наудачу отобранных из разных мест кипы. Хотя число волокон в пучке значительно меньше, чем в кипе, сам пучок содержит достаточно большое количество волокон, исчисляемое сотнями. В качестве другого примера можно указать на определение качества зерна по небольшой его пробе. И в этом случае число наудачу отобранных зерен мало сравнительно со всей массой зерна, но само по себе оно достаточно велико. Уже из приведенных примеров можно заключить, что для практики теорема Чебышева имеет неоценимое значение.
Теорема Бернулли
Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А равна р. Можно ли предвидеть, какова примерно будет относительная частота появлений события? Положительный ответ на этот вопрос дает теорема, доказанная Якобом Бернулли (опубликована в 1713 г.), которая получила название «закона больших чисел» и положила начало теории вероятностей как науке. Доказательство Бернулли было сложным; простое доказательство дано П. Л. Чебышевым в 1846 г. Теорема Бернулли. Если в каждом из п независимых испытаний вероятность р появления события А постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико. Другими словами, если e — сколь угодно малое положительное число, то при соблюдении условий теоремы имеет место равенство
Доказательство. Обозначим через Х 1дискретную случайную величину — число появлений события в первом испытании, через Х 2— во втором,..., Хп —в п- миспытании. Ясно, что каждая из величин может принять лишь два значения: 1 (событие А наступило) с вероятностью р и 0 (событие не появилось) с вероятностью 1— p = q. Можно ли применить к рассматриваемым величинам теорему Чебышева? Можно, если случайные величины попарно независимы и дисперсии их ограничены. Оба условия выполняются. Действительно, попарная независимость величин Х 1, Х 2,..., Хп следует из того, что испытания независимы. Дисперсия любой величины Хi (i= 1,2,..., п)равна произведению pq (Это следует из § 6 гл.III,если принять n =1); так как p+q = 1, то произведение pq не превышает (Известно, что произведение двух сомножителей, сумма которых есть величина постоянная, имеет наибольшее значение при равенстве сомножителей. Здесь сумма pi+qi =1, т.е. постоянна, поэтому при pi=qi= 1/2 произведение piqi имеет наибольшее значение и равно 1/4) 1/4 и, следовательно, дисперсии всех величин ограничены, например, числом С =1/4. Применяя теорему Чебышева (частный случай) к рассматриваемым величинам, имеем
Приняв во внимание, что математическое ожидание а каждой из величин Xi; (т. е. математическое ожидание числа появлений события в одном испытании) равно вероятности р наступления события (см. гл. VII, § 2, пример 2), получим
Остается показать, что дробь (Х 1 + Х 2 +...+ Хп) /n равна относительной частоте т/п появлений события А в испытаниях. Действительно, каждая из величин Х 1, Х 2 ,..., Хп при появлении события в соответствующем испытании принимает значение, равное единице; следовательно, сумма Х 1 + Х 2 +...+ Хп равна числу т появлений события в п испытаниях, а значит, (Х 1 + Х 2 +...+ Хп) /n=m/n. Учитывая это равенство, окончательно получим
Замечание. Было бы неправильным на основании теоремы Бернулли сделать вывод, что с ростом числа испытаний относительная частота неуклонно стремится к вероятности р; другими словами, из теоремы Бернулли не вытекает равенство Таким образом, сходимость относительной частоты т/п к вероятности р отличается от сходимости в смысле обычного анализа. Для того чтобы подчеркнуть это различие, вводят понятие «сходимости по вероятности»(Последовательность случайных величин Х 1 ,Х 2 ,... сходится по вероятности к случайной величине X, если для любого e> 0вероятность неравенства | Xn-X |< e при Итак, теорема Бернулли утверждает, что при
Как видим, теорема Бернулли объясняет, почему относительная частота при достаточно большом числе испытаний обладает свойством устойчивости и оправдывает статистическое определение вероятности (см. гл. I, § 6—7). Задачи 1. Сформулировать и записать теорему Чебышева, используя понятие «сходимости по вероятности». 2. Используя неравенство Чебышева, оценить вероятность того, что | Х—М (Х) |< 0, 1, если. D (X)= 0,001. Отв. P 3. Дано: Р (| Х—М (X)| < e) Отв. 0,2.
Глава десятая
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 550; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.172.250 (0.008 с.) |

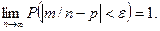
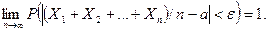
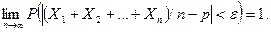
 В теореме речь идет лишь о вероятности того, что при достаточно большом числе испытаний относительная частота будет как угодно мало отличаться от постоянной вероятности появления события в каждом испытании.
В теореме речь идет лишь о вероятности того, что при достаточно большом числе испытаний относительная частота будет как угодно мало отличаться от постоянной вероятности появления события в каждом испытании. стремится к единице). Точнее, различие между указанными видами сходимости состоит в следующем: если т/п стремится при
стремится к единице). Точнее, различие между указанными видами сходимости состоит в следующем: если т/п стремится при  .
. O,9.
O,9.


