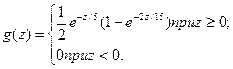Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция двух случайных аргументов. Распределение суммы независимых слагаемых. Устойчивость нормального распределенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если каждой паре возможных значений случайных величин X и Y соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов X и Y: Z = j (X, Y). Далее на примерах будет показано, как найти распределение функции Z = X + Y по известным распределениям слагаемых. Такая задача часто встречается на практике. Например, если X — погрешность показаний измерительного прибора (распределена нормально), Y — погрешность округления показаний до ближайшего деления шкалы (распределена равномерно), то возникает задача — найти закон распределения суммы погрешностей Z=X + Y. 1. Пусть X и Y —дискретные независимые случайные величины. Для того чтобы составить закон распределения функции Z = X + Y, надо найти все возможные значения Z и их вероятности. Пример 1. Дискретные независимые случайные величины заданы распределениями:
Составить распределение случайной величины Z = X+Y. Решение. Возможные значения Z есть суммы каждого возможного значения X со всеми возможными значениями Y: z 1 = 1 + 3 = 4; z 2 = 1 + 4 = 5; z 3 = 2 + 3 = 5; z 4 = 2 + 4 = 6. Найдем вероятности этих возможных значений. Для того чтобы Z = 4, достаточно, чтобы величина X приняла значение x 1 =1 и величина Y — значение y 1 = 3. Вероятности этих возможных значений, как следует из данных законов распределения, соответственно равны 0,4 и 0,2. Аргументы X и Y независимы, поэтому события Х= 1и Y = 3 независимы и, следовательно, вероятность их совместного наступления (т. е. вероятность события Z = 1+3 = 4) по теореме умножения равна 0,4*0,2 = 0,08. Аналогично найдем: P (Z= 1 + 4 = 5) = 0, 4 * 0, 8 = 0, 32; Р (Z = 2 + 3 = 5) = 0, 6 * 0, 2 = 0, 12; Р (Z = 2 + 4 = 6) = 0, 6 * 0, 8 = 0, 48. Напишем искомое распределение, сложив предварительно вероятности несовместных событий Z = z 2, Z = z 3(0,32+0,12 = 0,44):
Контроль: 0,08 + 0,44+0,48=1. 2. Пусть X и Y — непрерывные случайные величины. Доказано: если X и Y независимы, то плотность распределения g (z) суммы Z = X + Y (при условии, что плотность хотя бы одного из аргументов задана на интервале(
либо с помощью равносильного равенства
где f 1, f 2 — плотности распределения аргументов. Если возможные значения аргументов неотрицательны, то g (z)находят по формуле
либо по равносильной формуле
Плотность распределения суммы независимых случайных величин называют композицией. Закон распределения вероятностей называют устойчивым, если композиция таких законов есть тот же закон (отличающийся, вообще говоря, параметрами). Нормальный закон обладает свойством устойчивости: композиция нормальных законов также имеет нормальное распределение (математическое ожидание и дисперсия этой композиции равны соответственно суммам математических ожиданий и дисперсий слагаемых). Например, если X и Y — независимые случайные величины, распределенные нормально с математическими ожиданиями и дисперсиями, соответственно равными а 1 = З, а 2 = 4, D 1=1, D 2 = 0, 5, то композиция этих величин (т. е. плотность вероятности суммы Z = X + Y)также распределена нормально, причем математическое ожидание и дисперсия композиции соответственно равны а = 3 + 4 = 7; D =l +0,5=1,5. Пример 2. Независимые случайные величины X и Y заданы плотностями распределений: f (x) = f (y) = Найти композицию этих законов, т. е. плотность распределения случайной величины Z = X+Y. Решение. Возможные значения аргументов неотрицательны, Поэтому воспользуемся формулой (***)
Заметим, что здесь z Рекомендуем читателю для контроля убедиться, что
В следующих далее параграфах кратко описаны распределения, связанные с нормальным, которые будут использованы при изложении математической статистики.
Распределение «хи квадрат»
Пусть Xi (i = 1, 2 ,..., п)— нормальные независимые случайные величины, причем математическое ожиданиекаждой из них равно нулю, а среднее квадратическоеотклонение—единице. Тогда сумма квадратов этих величин
распределена по закону Плотность этого распределения
где
Отсюда видно, что распределение «хи квадрат» определяется одним параметром — числом степеней свободы k. С увеличением числа степеней свободы распределение медленно приближается к нормальному.
Распределение Стьюдента
Пусть Z —нормальная случайная величина, причем M (Z) = 0, s(Z) = 1, a V —независимая от Z величина, которая распределена по закону
имеет распределение, которое называют t- распределением или распределением Стьюдента (псевдоним английского статистика В. Госсета), с k степенями свободы. Итак, отношение нормированной нормальной величины к квадратному корню из независимой случайной величины, распределенной по закону «хи квадрат» с k степенями свободы, деленной на k, распределено по закону Стьюдента с k степенями свободы. С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному. Дополнительные сведения об этом распределении приведены далее (см. гл. XVI, § 16).
§ 15. Распределение F Фишера — Снедекора
Если U и V —независимые случайные величины, распределенные по закону
имеет распределение, которое называют распределением F Фишера—Снедекора со степенями свободы k 1и k 2 (иногда его обозначают через V 2). Плотность этого распределения
где
Мы видим, что распределение F определяется двумя параметрами—числами степеней свободы. Дополнительные сведения об этом распределении приведены далее (см. гл. XIX, § 8). Задачи 1. Найти математическое ожидание и дисперсию случайной величины X, зная ее плотность распределения: а) б) f (x) = 1 / 2 l при а — l Отв. a) М (Х)= 0, D (X) = l/2; б) М (Х) = а, D (X) = l 2 / 3. 2. Случайная величина X распределена нормально. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 6 и 2. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (4,8). Отв. 0,6826. 3. Случайная величина распределена нормально. Среднее квадратическое отклонение этой величины равно 0,4. Найти вероятность того, что отклонение случайной величины от ее математического ожидания по абсолютной величине будет меньше 0,3. Отв. 0,5468. 4. Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением s=1 мм и математическим ожиданием а = 0. Найти вероятность того, что из двух независимых наблюдений ошибка хотя бы одного из них не превзойдет по абсолютной величине 1,28 мм. Отв. 0,96. 5. Валики, изготовляемые автоматом, считаются стандартными, если отклонение диаметра валика от проектного размера не превышает 2 мм. Случайные отклонения диаметра валиков подчиняются нормальному закону со средним квадратическим отклонением s = 1,6 мм и математическим ожиданием а = 0. Сколько процентов стандартных валиков изготовляет автомат? Отв. Примерно 79%. 6. Дискретная случайная величина X задана законом распределения:
а)
б)
Найти закон распределения случайной величины Y=X 4.
Отв. а)
б)
7. Непрерывная случайная величина X задана плотностью распределения f (x). Найти дифференциальную функцию g (y)случайной величины Y, если: а) Y = Х+ 1( Отв. a) g (у) =f (y— 1)( б ) g (y) = 1 / 2 f (y/ 2)(— 2 а < у < 2 а). 8. Независимые дискретные случайные величины заданы следующими законами распределения:
Найти законы распределения функций: a) Z = X+Y; б) Z = XY.
Отв. a)
б)
9. Независимые случайные величины X и Y заданы плотностями распределений
Найти композицию этих законов, т. е. плотность распределения случайной величины Z = X+Y. Отв.
Глава тринадцатая ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 2360; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.119.61 (0.012 с.) |

 ) одной формулой) может быть найдена с помощью равенства
) одной формулой) может быть найдена с помощью равенства (*)
(*) (**)
(**) (***)
(***) (****)
(****) ;
; .
.
 0, так как Z=X+Y и, по условию, возможные значения X и Y неотрицательны.
0, так как Z=X+Y и, по условию, возможные значения X и Y неотрицательны.

 («хи квадрат») с k = п степенями свободы; если же эти величины связаны одним линейным соотношением, например
(«хи квадрат») с k = п степенями свободы; если же эти величины связаны одним линейным соотношением, например 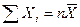 , то число степеней свободы k=n- 1.
, то число степеней свободы k=n- 1.
 — гамма-функция; в частности,
— гамма-функция; в частности,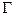 (n+ 1) =n!.
(n+ 1) =n!. (*)
(*)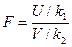 (*)
(*)
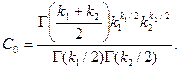
 при остальных значениях x;
при остальных значениях x; x
x  < х <
< х <  ); б) Y = 2 Х (— а < x < а).
); б) Y = 2 Х (— а < x < а).