Переходные вероятности. Матрица перехода

Однородной называют цепь Маркова, если услов­ная вероятность р_ij (s) (перехода из состояния i в состоя­ние j) не зависит от номера испытания. Поэтому вместо р_ij (s) пишут просто р_ij.

Пример. Случайное блуждание. Пусть на прямой Ох в точке с целочисленной координатой х=п находится материальная частица. В определенные моменты времени, t ₁, t ₂, t₃, … частица испытывает толчки. Под действием толчка частица с вероятностью р смещается на единицу вправо и с вероятностью 1—р —на единицу влево. Ясно, что положение (координата) частицы после толчка зави­сит от того, где находилась частица после непосредственно предшест­вующего толчка, и не зависит от того, как она двигалась под дейст­вием остальных предшествующих толчков.

Таким образом, случайное блуждание—пример однородной цепи Маркова с дискретным временем.

Далее ограничимся элементами теории конечных одно­родных цепей Маркова.

Переходной вероятностью р_ij называют условную вероятность того, что из состояния i (в котором система оказалась в результате некоторого испытания, безраз­лично какого номера) в итоге следующего испытания система перейдет в состояние j.

Таким образом, в обозначении р_ij первый индекс ука­зывает номер предшествующего, а второй—номер после­дующего состояния. Например, p ₁₁—вероятность «пере­хода» из первого состояния в первое; р _{2 3} —вероятность перехода из второго состояния в третье.

Пусть число состояний конечно и равно k.

Матрицей перехода системы называют матрицу, ко­торая содержит все переходные вероятности этой сис­темы:

Так как в каждой строке матрицы помещены вероят­ности событий (перехода из одного и того же состояния i в любое возможное состояние j). которые образуют полную группу, то сумма вероятностей этих событий равна единице. Другими словами, сумма переходных вероятностей каждой строки матрицы перехода равна единице:

Приведем пример матрицы перехода системы, которая может находиться в трех состояниях:

Здесь р ₁₁=0,5—вероятность перехода из состояния j =1 в это же состояние j =1; р ₂₁ = 0,4 — вероятность перехода из состояния i =2 в состояние j =2. Анало­гичный смысл имеют остальные элементы матрицы.

Равенство Маркова

Обозначим через Р_ij (п) вероятность того, что в результате п шагов (испытаний) система перейдет из состояния i в состояние j. Например, Р _{2 5} (10) — вероят­ность перехода за 10 шагов из второго состояния в пятое. Подчеркнем, что при п = 1 получим переходные веро­ятности

Р_ij (1) =p_ij.

Поставим перед собой задачу: зная переходные веро­ятности Р_ij, найти вероятности Р_ij (п) перехода системы из состояния i в состояние j за п шагов. С этой целью введем в рассмотрение промежуточное (между i и j) состояние r. Другими словами, будем считать, что из первоначального состояния i за т шагов система перей­дет в промежуточное состояние r с вероятностью Р_ir (т), после чего за оставшиеся п—т шагов из промежуточного состояния r она перейдет в конечное состояние j с веро­ятностью Р_{rj (} п—т).

По формуле полной вероятности,

(*)

Эту формулу называют равенством Маркова.

Пояснение. Введем обозначения: A —интересую­щее нас событие (за п шагов система перейдет из началь­ного состояния i в конечное состояние j), следовательно, P (A)= P_ij (n); В_r (r = 1, 2,..., k)—гипотезы (за т шагов система перейдет из первоначального состояния (в про­межуточное состояние r), следовательно, Р (В_r)= Р_ir (m); Р_Br (A)—условная вероятность наступления А при усло­вии, что имела место гипотеза В_r (за п—т шагов система перейдет из промежуточного состояния r в конечное состояние j), следовательно, Р_Br (A) = Р_rj (п—m). По формуле полной вероятности,

,

или в принятых нами обозначениях

,

что совпадает с формулой (*) Маркова.

Покажем, что, зная все переходные вероятности р_ij = Р_ij (1), т. е. зная матрицу τ ₁ перехода из состояния в состояние за один шаг, можно найти вероятности Р_ij (2) перехода из состояния в состояние за два шага, следо­вательно, и саму матрицу перехода τ ₂ по известной матрице τ ₂, можно найти матрицу τ₃ перехода из состоя­ния в состояние за 3 шага, и т.д.

Действительно, положив n =2, m =1 в равенстве Маркова

,

получим

или

(**)

Таким образом, по формуле (**) можно найти все вероятности Р _ij (2), следовательно, и саму матрицу τ ₂.Поскольку непосредственное использование формулы (**) оказывается утомительным, а матричное исчисление ведет к цели быстрее, напишем вытекающее из (**) соотноше­ние в матричной форме:

τ ₂= τ ₁ τ ₁= τ ₂²

Положив n =3, m =2 в (*), аналогично получим

τ₃ = τ ₁ τ ₂= τ ₁ τ ₁²= τ ₁ ³.

В общем случае

τ_n = τ ₁ ⁿ

Пример. Задана матрица перехода Найти матрицу перехода

Решение. Воспользуемся формулой: τ ₂= τ ₁²:

Перемножив матрицы, окончательно получим

Задачи

1. Задана матрица перехода Найти матрицу перехода τ ₂.

Отв.

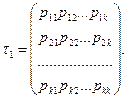
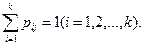
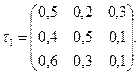
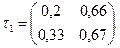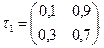2. Задана матрица перехода Найти матрицу перехода τ ³.

Отв.

 

ЧАСТЬ ПЯТАЯ СЛУЧАЙНЫЕ ФУНКЦИИ