
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы расчета сводных характеристикСодержание книги
Поиск на нашем сайте
ВЫБОРКИ § 1. Условные варианты Предположим, что варианты выборки расположены в возрастающем порядке, т. е. в виде вариационного ряда. Равноотстоящими называют варианты, которые образуют арифметическую прогрессию с разностью h. Условными называют варианты, определяемые равенством ui= (xi-C) /h, где С —ложный нуль (новое начало отсчета); h — шаг, т. е. разность между любыми двумя соседними первоначальными вариантами (новая единица масштаба). Упрощенные методы расчета сводных характеристик выборки основаны на замене первоначальных вариант условными. Покажем, что если вариационный ряд состоит из равноотстоящих вариант с шагом h, то условные варианты есть целые числа. Действительно, выберем в качестве ложного нуля произвольную варианту, например хт, Тогда
Так как i и m- целые числа, то их разность i-m = иi -также целое число. Замечание 1. В качестве ложного нуля можно принять любую варианту. Максимальная простота вычислений достигается, если выбрать в качестве ложного нуля варианту, которая расположена примерно в середине вариационного ряда (часто такая варианта имеет наибольшую частоту). Замечание 2. Варианте, которая принята в качестве ложного нуля, соответствует условная варианта, равная нулю. Пример. Найти условные варианты статистического распределения: Решение. Выберем в качестве ложного нуля варианту 33,6 (этаварианта расположена в середине вариационного ряда). Найдем шаг: h = 28,6 —23,6 = 5. Найдем условную варианту: u 1 = (xi-C) /h = (23,6 —33,6)/5 = -2. Аналогично получим: u 2= - 1, u 3 = 0, u 4 =1, u 5 = 2. Мы видим, что условные варианты — небольшие целые числа. Разумеется, оперировать с ними проще, чем с первоначальными вариантами.
Обычные, начальные и центральные эмпирические моменты Для вычисления сводных характеристик выборки удобно пользоваться эмпирическими моментами, определения которых аналогичны определениям соответствующих теоретических моментов (см. гл. VIII, § 10). В отличие от теоретических эмпирические моменты вычисляют по данным наблюдений. Обычным эмпирическим моментом порядка k называют среднее значение k -x степеней разностей xi - С:
где xi- наблюдаемая варианта, ni- частота варианты,
Начальным эмпирическим моментом порядка k называют обычный момент порядка k при С = 0
В частности,
т, е. начальный эмпирический момент первого порядка равен выборочной средней. Центральным эмпирическим моментом порядка k называют обычный момент порядка k при С =
В частности,
т. е. центральный эмпирический момент второго порядка равен выборочной дисперсии. Легко выразить центральные моменты через обычные (рекомендуем читателю сделать это самостоятельно):
Условные эмпирические моменты. Отыскание центральных моментов по условным Вычисление центральных моментов требует довольно громоздких вычислений. Чтобы упростить расчеты, заменяют первоначальные варианты условными. Условным эмпирическим моментом порядка k называют начальный момент порядка k, вычисленный для условных вариант:
В частности,
Отсюда
Таким образом, для того чтобы найти выборочную среднюю, достаточно вычислить условный момент первого порядка, умножить его на h и к результату прибавить ложный нуль С. Выразим обычные моменты через условные:
Отсюда
Таким образом, для того чтобы найти обычный момент порядка k, достаточно условный момент того же порядка умножить на hk. Найдя же обычные моменты, легко найти центральные моменты по равенствам (**) и (***) предыдущего параграфа. В итоге получим удобные для вычислений формулы, выражающие центральные моменты через условные:
В частности, в силу (**) и соотношения (*) предыдущего параграфа получим формулу для вычисления выборочной дисперсии по условным моментам первого и второго порядков
Техника вычислений центральных моментов по условным описана далее.
|
|||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 614; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.67.57 (0.007 с.) |

 .
.
 - объем выборки, С - произвольное постоянное число (ложный нуль).
- объем выборки, С - произвольное постоянное число (ложный нуль). .
. ,
,
 .
.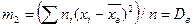 , (*)
, (*) , (**)
, (**)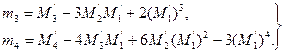 (***)
(***)
 .
. .
.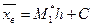 . (*)
. (*)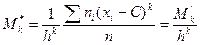 .
.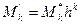 .
.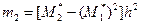 , (**)
, (**) (***)
(***)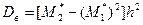 . (****)
. (****)


