
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разыгрывание полной группы событийСодержание книги
Поиск на нашем сайте
Разыгрывание полной группы п (п > 2) несовместных событий A 1, A 2,…, An. вероятности которых р 1, р 2,…, рn известны, можно свести к разыгрыванию дискретной случайной величины Х со следующим законом распределения (для определенности примем х 1 = 1, х 2 = 2, …, хn = n);
Действительно, достаточно считать, что если в испытании величина Х приняла значение хi = i (i= 1, 2, …, п), то наступило событие Ai,. Справедливость этого утверждения следует из того, что число п возможных значений Х равно числу событий полной группы и вероятности возможных значений хi, и соответствующихим событий Ai одинаковы: Р (X == хi) = Р (Ai)=рi,. Таким образом, появление в испытании события A равносильно событию, состоящему в том, что дискретная случайная величина Х приняла возможное значение хi. Правило. Для того чтобы разыграть испытания, в каждом из которых наступает одно из событий А 1, А 2,…, Аn полной группы, вероятности которых р 1, р 2,…, рn известны, достаточно разыграть (по правилу § 4) дискретную случайную величину Х со следующим законом распределения:
Если в испытании величина Х приняла возможное значение хi = i, то наступило событие Аi. Пример 1. Заданы вероятности четырех событий, образующих полную группу: р 1 =Р (A 1)=0,19, р 2 =Р (A 2)=0,21, р3=Р (A3)=0,34 р4=Р (A4)=0,26. Разыграть 5 испытаний, в каждом из которых появляется одно из четырех заданных событий. Решение. В соответствии с правилом, приведенным в настоящем параграфе, надо разыграть дискретную случайную величину X, закон распределения которой
По правилу § 4 разобьем интервал (0,1) на четыре частичных интервала: ∆ 1—(0; 0,19), ∆ 2,—(0,19; 0,40), ∆3,—(0,40; 0,74), ∆4 — (0,74; 1). Выберем из таблицы приложения 9 пять случайных чисел, например: 0,66; 0,31; 0,85; 0,63; 0,73. Так как случайное число r 1=0,66 gринадлежит интервалу ∆3, то Х=3, следовательно, наступило событие А3,. Аналогично найдем остальные события. Итак, искомая последовательность событий такова: А3, А 2, А4, А3, А3. Пример 2. События А и В независимы и совместны. Разыграть 6 испытаний, в каждом из которых вероятность появления события А равна 0,6, а вероятность появления события В равна 0,2. Решение. Возможны 4 исхода испытания: А 1 =АВ, причем в силу независимости событий Р (АВ) = Р (А) -Р (В)=0.6·0.2=0,12; А 2= А3 = А4 = Таким образом, задача сведена к разыгрыванию полной группы четырех событий: А 1с вероятностью р 1=0,12, А 2 с вероятностью р 2=0,48, А, с вероятностью р3 = 0,08 и А4 свероятностью р4 =0,32. В свою очередь, в соответствии с правилом настоящего параграфа эта задача сводится к разыгрыванию дискретной случайной величины X, закон распределения которой
Используем правило § 4. Выберем 6 случайных чисел, например; 0,45; 0,65; 0,06; 0,59; 0,33; 0,70. Построим частичные интервалы: ∆ 1—(0; 0,12), ∆ 2—(0,12; 0,60); ∆3 —(0,60; 0,68); ∆4 —(0,68; 1). Случайное число r 1=0,45 принадлежит интервалу ∆ 2, поэтому наступило событие А 2= Итак, искомая последовательность исходов разыгранных испытаний такова: Пример 3. События A и В зависимы и совместны. Разыграть 4 испытания, в каждом из которых заданы вероятности Р (A)=0,6; Р (В)=0,6; Р (AВ)=0,5. Решение. Возможны 4 исхода испытания: А 1 =АВ, причем, по условию, Р (АВ)=0,5; А 2= А3 = А4 = Таким образом, задача сведена к разыгрыванию полной группы четырех событий: А 1с вероятностью 0,5, А 2 с вероятностью 0,3, А3 с вероятностью 0,1 и А4 с вероятностью 0,1. Рекомендуем закончить решение самостоятельно, считая для определенности, что выбраны случайные числа: 0,65; 0,06; 0,59; 0,33. Для контроля приводим ответ: Пояснение. Так как А=АВ+ Аналогично получим, что Р (
Разыгрывание непрерывной случайной величины. Метод обратных функций Пусть требуется разыграть непрерывную случайную величину X, т. е. получить последовательность ее возможных значений xi (i= 1,2,...), зная функцию распределения F (х). Теорема. Если ri,— случайное число, то возможное значение xi разыгрываемой непрерывной случайной величины Х с заданной функцией распределения F (х), соответствующееri, является корнем уравнения F (хi) =ri. (») Доказательство. Пусть выбрано случайное число ri (0≤ ri <1). Так как в интервале всех возможных значений Х функция распределения F (х) монотонно возрастает от 0 до 1, то в этом интервале существует, причем только одно, такое значение аргумента хi,, при котором функция распределения примет значение ri. Другими словами, уравнение (*) имеет единственное решение хi=F- 1(ri), где F- 1 — функция, обратная функции у=F (х). Докажем теперь, что корень хi уравнения (*) есть возможное значение такой непрерывной случайной величины (временно обозначим ее через ξ, а потом убедимся, что ξ=Х). С этой целью докажем, что вероятность попадания ξ в интервал, например (с, d), принадлежащий интервалу всех возможных значений X, равна приращению функции распределения F (х) на этом интервале: Р (с<ξ<d) =F (d) —F (с). Действительно, так как F (х) — монотонно возрастающая функция в интервале всех возможных значений X, то в этом интервале большим значениям аргумента соответствуют большие значения функции, и обратно. Поэтому, если с < хi < d, то F (c) <ri<F (d),и обратно [учтено, что в силу (*) F (хi)= ri ]. Из этих неравенств следует, чтоесли случайная величина ξ заключена в интервале с< ξ < d, ξ (**) то случайная величина R заключена в интервале F (с) <R<F (d), (***) и обратно. Таким образом, неравенства(**) и (***) равносильны, а, значит, и равновероятны: Р (с<ξ<d) =Р [ F (с) <R<F (d)]. (****) Так как величина R распределена равномерно в интервале (0,1), то вероятность попадания R в некоторый интервал, принадлежащий интервалу (0,1), равна его длине (см. гл. XI, § 6, замечание). В частности, Р [ F (с) <R<F (d) ] =F (d) - F (с). Следовательно, соотношение (****) можно записать в виде Р (с<ξ<d) = F (d) - F (с). Итак, вероятность попадания ξ в интервал (с,d) равна приращению функции распределения F (х) на этом интервале, а это означает, что ξ=Х. Другими словами, числа хi, определяемые формулой (*), есть возможные значения величины Х с заданной функцией распределения F (х), что и требовалось доказать. Правило 1. Для того чтобы найти возможное значение хi, непрерывной случайной величины X, зная ее функцию распределения F (х), надо выбрать случайное число ri приравнять его функции распределения и решить относительно хi, полученное уравнение F (хi) = ri. Замечание 1. Если решить это уравнение в явном видене удается, то прибегают к графическим или численным методам. Пример I. Разыграть 3 возможных значения непрерывной случайной величины X, распределенной равномерно в интервале (2, 10). Решение. Напишем функцию распределения величины X, распределенной равномерно в интервале (а, b) (см. гл. XI, § 3, пример): F (х) = (х-а) / (b-а) . По условию, а = 2, b =10, следовательно, F (х) = (х- 2) / 8. Используя правило настоящего параграфа, напишем уравнение для отыскания возможных значений хi, для чего приравняем функцию распределения случайному числу: (хi -2) /8=ri. Отсюда хi=8 ri+ 2. Выберем 3 случайных числа, например, ri =0,11, ri =0,17, ri =0,66. Подставим эти числа в уравнение, разрешенное относительно хi, в итоге получим соответствующие возможные значения X: х 1=8·0,11+2==2,88; х 2=1.36; х3= 7,28. Пример 2. Непрерывная случайная величина Х распределенапопоказательному закону, заданному функцией распределения (параметр λ > 0 известен) F (х) = 1 - е-λх (х>0) . Требуется найти явную формулу для разыгрывания возможных значений X. Решение. Используя правило настоящего параграфа, напишем уравнение 1 - е-λхi Решим это уравнение относительно хi: е-λхi= 1 - ri, или -λхi=ln (1 - ri). Отсюда хi = 1п (1 – ri)/λ . Случайное число ri заключено в интервале (0,1); следовательно, число 1 - ri, также случайное и принадлежит интервалу (0,1). Другими словами, величины R и 1 - R распределены одинаково. Поэтому для отыскания хi можно воспользоваться более простой формулой: xi=-ln ri /λ. Замечание 2. Известно, что (см. гл. XI, §3)
В частности,
Отсюда следует, что если известна плотность вероятности f (x), то для разыгрывания Х можно вместоуравнений F (xi)= ri решить относительно xi уравнение
Правило 2. Для того чтобы найти возможное значение хi (непрерывной случайной величины X, зная ее плотность вероятности f (x) надо выбрать случайное число ri и решить относительно хi, уравнение
Или уравнение
где а— наименьшее конечное возможное значение X. Пример 3. Задана плотность вероятности непрерывной случайной величины Х f (х) =λ (1 —λх /2) в интервале (0; 2/λ); вне этого интервала f (х) = 0. Требуется найти явную формулу для разыгрывания возможных значений X. Решение. Напишем в соответствии с правилом 2 уравнение
Выполнив интегрирование и решив полученное квадратное уравнение относительно хi, окончательно получим
Метод суперпозиции Пусть функция распределения разыгрываемой случайной величины Х может быть представлена в виде линейной комбинации двух функций распределения: F (х) =С 1 F 1(х) + С 2 F 2(х)(С 1>0, С2>0). При х→∞ каждая из функций распределения стремится к единице, поэтому С1+С2=1. Введем вспомогательную дискретную случайную величину Z. с законом распределения
Мы видим, что Р(Z -1)=С1, Р(Z =2)=С2,. (*) Выберем два независимых случайных числа r 1 и r 2По числу r 1 разыгрываем возможное значение Z. (см. § 4). Если окажется, что Z =1, то ищут искомое возможное значение Х из уравнения F 1(х) =r 2, если Z =2, то решают относительно х уравнение F 2(х) =r 2. Докажем, что функция распределения разыгрываемой случайной величины равна заданной функции распределения. Воспользуемся формулой полной вероятности (см. гл. IV, § 2) Р (А) =Р (В 1) РB 1(А) +Р (В 2) РB 2(A). Обозначим через А событие Х < х; тогда Р (А) =Р (Х<х) =F (х). (**) Рассмотрим гипотезы В 1: Z=1 и В 2: Z =2. Вероятности этих гипотез в силу (*): Р (В 1)= Р (Z =1)= С 1 и Р (В 2) =Р (Z=2) =С 2. (***) Условные вероятности появления события А соответственно равны: PB 1(А)= РB 1(X<х)= F 1(х) и PB 2(А)= РB 2(X<х)= F 2(х) (****) Подставив (**), (***) и (****) в формулу полной вероятности, окончательно получим F (х) =С 1 F 1(х) +С 2 F 2(х), что и требовалось доказать. Замечание. Метод суперпозиции обобщается на n слагаемых функций распределения. Правило. Для того чтобы разыграть возможное значение случайной величины X, функция распределения которой F (х) =С 1 F 1(х) +С 2 F 2(х), где С 1>0, С 2>0 и С 1+ С 2 = 1, надо выбрать два независимых случайных числа r 1 и r 2и по случайному числу r 1 разыграть возможное значение вспомогательной дискретной случайной величины Z. (по правилу § 4):
Если окажется, что Z =1, то решают относительно х уравнение F 1(х) =r 2, если Z =2, то решают уравнение F 2(х) =r 2. Пример. Найти явные формулы для разыгрывания непрерывной случайной величины X, заданной функцией распределения F (х) = 1—0,25(е- 2 x+ 3 е-х), 0<х<∞. Решение. Воспользуемся методом суперпозиции, длячегопредставим заданную функцию в виде F (х) = 0,25(1 - е- 2 x)+0,75(1 -е-х). Таким образом, можно принять: F 1(х) = 1 - е- 2 x, F 2(х) = 1 -е-х, C 1=0.25, C 2=0,75. Введем в рассмотрение вспомогательную дискретнуюслучайнуювеличину Z с законом распределения
Выберем независимые случайные числа r 1и r 2. Разыграем Z по случайному числу r 1, для чего по правилу § 4 построим частичные интервалы ∆ 1—(0; 0,25), ∆ 2—(0,25; 1). Если r 1<0,25, то Z =1,если r 1 ≥ 0,25, то Z =2. Итак, возможное значение Х находят, решая относительно х уравнение 1 - е- 2 х = r 2, если r 1<0,25; или 1 - е-x=r 2, если r 1 ≥ 0,25. Используя решение примера 2 (см. § 7), в котором была найдена явная формула х= - (1/ λ) 1п r для разыгрывания возможных значений показательного распределения с заданным параметром λ, окончательно получим: x = - (1/2) 1п r 2, если r 1 < 0,25; х= - 1п r 2, если r 1 ≥ 0,25.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.67.56 (0.01 с.) |

 , причем Р (
, причем Р (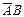 , причем Р (
, причем Р ( , причем Р (
, причем Р (








