
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представление стационарной случайной функции в виде гармонических колебаний со случайными амплитудами и случайными фазамиСодержание книги
Поиск на нашем сайте
В этой главе вводится новая характеристика стационарной случайной функции— спектральная плотность, которая упрощает теоретические и практические расчеты. В частности, используяее, можно найти характеристики выходной функции стационарной линейной динамической системы по известным характеристикам входной функции (см. § 8). Далее будет показано, что стационарную случайную функцию, вообще говоря, можно представить в виде гармонических колебаний со случайными амплитудами и случайными фазами. 1. Рассмотрим случайную функцию вида Z (t)= U cos ωt + V sm ωt, (*) где ω —постоянное действительное число; U и V— некоррелированные случайные величины с математическими ожиданиями, равными нулю, и одинаковыми дисперсиями: mu=mv= 0, Du=Dv=D. Преобразуем правую часть соотношения (*):
Положив U/V = tg φ и выполнив элементарные выкладки, получим
где φ = arctg(U/V). Отсюда следует, что случайную функцию Z (t)= U cos ωt+V sm ωt можно истолковать как гармоническое колебание со случайной амплитудой Заметим, что, по допущению, mu=mv= 0, поэтому U и V— центрированные случайные величины: Легко убедиться, что mz (t) = 0. Следовательно, Z (t) — центрированная случайная функция:
Покажем, что Z(t)= U cos ωt + V sin ωt — стационарная случайная функция. Действительно, математическое ожидание mz (t)=0, т.е. постоянно при всех значениях аргумента. Найдем корреляционную функцию, приняв во внимание, что
Итак, корреляционная функция случайной функции Z (t) зависит только от разности аргументов, а ее математическое ожидание постоянно. Следовательно, Z (t) — стационарная случайная функция, что и требовалось доказать. 2. Рассмотрим теперь случайную функцию Х (t), которая является суммой конечного числа слагаемых вида (*):
где случайные величины Ui и V i, не коррелированы,ихматематические ожидания равны нулю и дисперсии величин с одинаковыми индексами равны между собой: D (Ui) =D (Vi) =D. Заметим, что Х (t) — центрированная функция, т.е.
Докажем, что функция X (t) вида (**)—стационарная. Действительно, математическое ожидание mx (t) = 0при всех значениях аргумента, т.е. постоянно. Кроме того, слагаемые суммы (**) попарно не коррелированы (см. далее пояснение), поэтому корреляционная функция этой суммы равна сумме корреляционных функций слагаемых (см. гл. XXIII, § 15, следствие 1 из теоремы 2). В п. 1 доказано, что корреляционная функция каждого слагаемого (**) зависит только от разности аргументов t 2 – t 1. Следовательно, корреляционная функция суммы (**) также зависит только от разности аргументов:
При выкладках следует учесть, что, по условию, или
где τ= t 2 – t 1. Таким образом, случайная функция Х (t) вида (**) есть стационарная функция (разумеется, должны выполняться условия, указанные в п. 2). Принимая во внимание, что (см. п. 1)
где φ =arc t g(Ui/Vi), заключаем,что сумму (**) можнозаписать в виде
Итак, если случайная функция Х (t) может быть представлена в виде суммы гармоник различных частот со случайными амплитудами и случайными фазами, то Х(t)— стационарная функция. Спектральным разложением стационарной случайной функции называют представление этой функции в виде суммы гармонических колебаний различных частот со случайными амплитудами и случайными фазами. Пояснение. Покажем, что слагаемые суммы (**) попарно не коррелированы. Для простоты, не теряя общности доказательства, ограничимся двумя слагаемыми: X 1(t)= U 1cos ω 1 t + V 1sm ω 1 t и X 2(t)= U 2cos ω 2 t + V 2sm ω 2 t Убедимся, что их взаимная корреляционная функция равна нулю и, следовательно, они не коррелированы (см. гл. XXIII, § 12):
Выполнив умножение и вынеся неслучайные множители за знак математического ожидания, найдем
Случайные величины U 1, U 2, V 1, V 2 попарно не коррелированы, поэтому их корреляционные моменты равны нулю; отсюда следует, что все математические ожидания парных произведений этих величин равны нулю. Например, корреляционный момент величин U 1 и U 2 равен нулю: Итак, взаимная корреляционная функция
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 488; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |



 случайной фазой ωt +arctg(U/V) и частотой ω.
случайной фазой ωt +arctg(U/V) и частотой ω.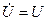 и
и 

 Выполнив элементарные выкладки *, получим
Выполнив элементарные выкладки *, получим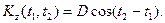
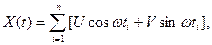 (**)
(**)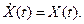 Действительно, математическое ожидание каждого слагаемого суммы (**) равно нулю; следовательно, математическое ожидание mx (t) этой суммы также равно нулю и, значит,
Действительно, математическое ожидание каждого слагаемого суммы (**) равно нулю; следовательно, математическое ожидание mx (t) этой суммы также равно нулю и, значит,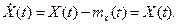

 а так как
а так как 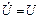 ,
,  , то
, то  . Случайные величины U и V не коррелированы, поэтомуих корреляционный момент
. Случайные величины U и V не коррелированы, поэтомуих корреляционный момент 
 (***)
(***)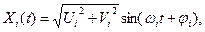
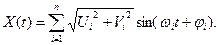

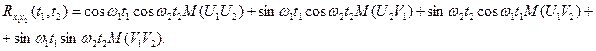
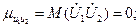 так как эти величины центрированные (см. п. 1), то M (U 1 U 2) =0.
так как эти величины центрированные (см. п. 1), то M (U 1 U 2) =0.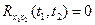 , что и требовалось доказать.
, что и требовалось доказать.


