
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых известны (независимые выборки)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть генеральные совокупности Х и У распределены нормально, причем их дисперсии известны (например, из предшествующего опыта или найдены теоретически). По независимым выборкам, объемы которых соответственно равны n и m, извлеченным из этих совокупностей, найдены выборочные средние Требуется по выборочным средним при заданном уровне значимости α проверить нулевую гипотезу, состоящую в том, что генеральные средние (математические ожидания) рассматриваемых совокупностей равны между собой, т. е. Н0:М(Х)==М(У). Учитывая, что выборочные средние являются несмещенными оценками генеральных средних (см. гл. XV, § 5), т. е. М ( Н0:М(
Таким образом, требуется проверить, что математические ожидания выборочных средних равны между собой. Такая задача ставится потому, что, как правило, выборочные средние оказываются различными. Возникает вопрос: значимо или незначимо различаются выборочные средние? Если окажется, что нулевая гипотеза справедлива, т. е. генеральные средние одинаковы, то различие выборочных средних незначимо и объясняется случайными причинами и, в частности, случайным отбором объектов выборки. Например, если физические величины А и В имеют одинаковые истинные размеры, а средние арифметические Если нулевая гипотеза отвергнута, т. е. генеральные средние неодинаковы, то различие выборочных средних значимо и не может быть объяснено случайными причинами, а объясняется тем, что сами генеральные средние (математические ожидания) различны. Например, если среднее арифметическое В качестве критерия проверки нулевой гипотезы примем случайную величину
Эта величина случайная, потому что в различных опытах Пояснение. По определению среднего квадратического отклонения, На основании свойства 4 (см. гл. VIII, § 5), D( По формуле (*) (см. гл. VIII, § 9), D( Следовательно,
Критерий Z—нормированная нормальная случайная величина. Действительно, величина Z распределена нормально, так как является линейной комбинацией нормально распределенных величин Критическая область строится в зависимости от вида конкурирующей гипотезы.
Первый случай. Нулевая гипотеза Н0: М(X) = М (Y). Конкурирующая гипотеза Н1: М(Х)≠М(У). В этом случае строят двустороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости α.
Наибольшая мощность критерия (вероятность попадания критерия в критическую область при справедливости конкурирующей гипотезы) достигается тогда, когда «левая» и «правая» критические точки выбраны так,что вероятность попадания критерия в каждый из двух интервалов критической области равна α/2:
Р (Z < zлев. кр) = α/2, Р (Z > zправ. кр) = α/2.
Поскольку Z—нормированная нормальная величина, а распределение такой величины симметрично относительно нуля, критические точки симметричны относительно нуля. Таким образом, если обозначить правую границу двусторонней критической области через zкр, то левая граница равна— zкр (рис. 25). Итак, достаточно найти правую границу, чтобы найти саму двустороннюю критическую область Z < — zкр, Z > zкр и область принятия нулевой гипотезы (—zкр, zкр). Покажем, как найти zкр —правую границу двусторонней критической области, пользуясь функцией Лапласа Ф(z). Известно, что функция Лапласа определяет вероятность попадания нормированной нормальной случайной величины, например Z, в интервал (0, z): Р(0<Z<z) = Ф(z). (**) Так как распределение Z симметрично относительно нуля, то вероятность попадания Z в интервал (0, ∞) равна 1/2. Следовательно, если разбить этот интервал точкой zкр на интервалы (0, zкр) и (zкр, ∞), то, по теореме сложения, Р (0 < Z < zкр) + Р (Z > zкр) = 1/2. (***) В силу (*) и (**) получим Ф(zкр)+α/2=1/2. Следовательно, Ф(zкр)=(1-α)/2. Отсюда заключаем: для того чтобы найти правую границу двусторонней критической области (zкр), достаточно найти значение аргумента функции Лапласа, которому соответствует значение функции, равное (1—α)/2. Тогда двусторонняя критическая область определяется неравенствами Z < — zкр, Z > zкр. или равносильным неравенством |Z| > zкр, а область принятия нулевой гипотезы—неравенством — zкр < Z < zкр, или равносильным неравенством |Z|< zкр. Обозначим значение критерия, вычисленное по данным наблюдений, через Zнабл и сформулируем правило проверки нулевой гипотезы. Правило 1. Для того чтобы при заданном уровне значимости α проверить нулевую гипотезу H0: М (X) = М (Y) о равенстве математических ожиданий двух нормальных генеральных совокупностей с известными дисперсиями при конкурирующей гипотезе Н1: М (Х) ≠ М (Y), надо вычислить наблюденное значение критерия Если |Zнабл| < zкр — нет оснований отвергнуть нулевую гипотезу. Если |Zнабл| > zкр —нулевую гипотезу отвергают. Пример 1. По двум независимым выборкам, объемы которых соответственно равны n==60 и m =50, извлеченным из нормальных генеральных совокупностей, найдены выборочные средние Решение. Найдем наблюдаемое значение критерия:
По условию, конкурирующая гипотеза имеет вид М (Х) ≠ М (Y), поэтому критическая область—двусторонняя. Найдем правую критическую точку: Ф(zкр)=(1—α)/2=(1—0,01)/2=0,495. По таблице функции Лапласа (см. приложение 2) находим zкр = 2,58. Так как | Zнабл | > zкр —нулевую гипотезу отвергаем. Другими словами, выборочные средние различаются значимо.
Второй случай. Нулевая гипотеза Н0: М (X) = М (Y). Конкурирующая гипотеза Н1: М (X) > М (Y).
На практике такой случай имеет место, если профессиональные соображения позволяют предположить, что генеральная средняя одной совокупности большегенеральной средней другой. Например, если введено усовершенствование технологического процесса, то естественно допустить, что оно приведет к увеличению выпуска продукции. В этом случае строят правостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости (рис. 26): Р(Z> zкр) = α. (****) Покажем, как найти критическую точку с помощью функции Лапласа. Воспользуемся соотношением (***): Р (0 < Z < zкр) + Р (Z > zкр) = 1/2. В силу (**) и (****) имеем Ф(zкр)+α=1/2. Следовательно, Ф(zкр) = (1-2α)/2. Отсюда заключаем: для того чтобы найти границу правосторонней критической области (zкр), достаточно найти значение аргумента функции Лапласа, которому соответствует значение функции, равное (1—2α)/2. Тогда правосторонняя критическая область определяется неравенством Z > zкр, а область принятия нулевой гипотезы — неравенством Z < zкр. Правило 2. Для того чтобы при заданном уровне значимости а проверить нулевую гипотезу Н0: М (X) = М (Y) о равенстве математических ожиданий двух нормальных генеральных совокупностей с известными дисперсиями при конкурирующей гипотезе Н1: М (X) > М (Y), надо вычислить наблюдавшееся значение критерия Если Zнабл < zкр —нет оснований отвергнуть нулевую гипотезу. Если Zнабл > zкр —нулевую гипотезу отвергают. Пример 2. По двум независимым выборкам, объемы которых соответственно равны n =10 и m ==10, извлеченным из нормальных генеральных совокупностей, найдены выборочные средние Решение. Найдем наблюдаемое значение критерия:
По условию, конкурирующая гипотеза имеет вид М (X) > М (Y), поэтому критическая область—правосторонняя. По таблице функции Лапласа находим zкр = 1,64. Так как Zнабл < zкр — нет оснований отвергнуть нулевую гипотезу. Другими словами, выборочные средние различаются незначимо.
Третий случай. Нулевая гипотеза Н0: М (X) = М (Y). Конкурирующая гипотеза Н1: М (X) > М (Y).
В этом случае строят левостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости (рис. 27): Р(Z< z’кр)= α. Приняв во внимание, что критерий Z распределен симметрично относительно нуля, заключаем, что искомая критическая точка z’кр симметрична такой точке zкр > 0, для которой Р (Z > zкр) = α,' т. е. z’кр = - zкр. Таким образом, для того чтобы найти точку z’кр, достаточно сначала найти «вспомогательную точку» zкр так, как описано во втором случае, а затем взять найденное значение со знаком минус. Тогда левосторонняя критическая область определяется неравенством Z <— zкр, а область принятия нулевой гипотезы—неравенством Z>— zкр. Правило 3. При конкурирующей гипотезе Н1: М (X) > М (Y) надо вычислить Zнабл и сначала по таблице функции Лапласа найти «вспомогательную точку» zкр по равенству Ф(zкр = (1—2α)/2, а затем положить z’кр = - zкр Если Zнабл < -zкр —нет оснований отвергнуть нулевую гипотезу. Если Zнабл > -zкр —нулевую гипотезу отвергают.
Пример 3. По двум независимым выборкам, объемы которых соответственно равны n==50 и m ==50, извлеченнымиз нормальных генеральных совокупностей, найдены выборочные средние Решение. Подставив данные задачи в формулу для вычисления наблюдаемого значения критерия, получим Zнабл = - 8. По условию, конкурирующая гипотеза имеет вид М (X) < М (Y), поэтому критическая область—левосторонняя. Найдем «вспомогательную точку» zкр: Ф (zкр) = (1-2α)/2 =(1-2·0,01)/2 = 0,49. По таблице функции Лапласа находим zкр =2,33. Следовательно, z’кр = — zкр = —2,33. Так как Zнабл <— zкр —нулевую гипотезу отвергаем. Другими словами, выборочная средняя
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 891; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.127.131 (0.01 с.) |

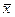 и
и 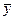 .
.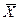 ) = М (X) и М (
) = М (X) и М (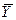 ) = М (Y), нулевую гипотезу можно записать так:
) = М (Y), нулевую гипотезу можно записать так: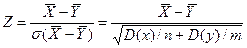 ,
, .
.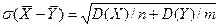 .
.
 и по таблице функции Лапласа найти критическую точку по равенству
и по таблице функции Лапласа найти критическую точку по равенству  .
. .
.
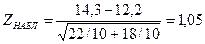 .
.



