
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка погрешности метода Монте—КарлоСодержание книги
Поиск на нашем сайте
Пусть для получения оценки а* математического ожидания а случайной величины Х было произведено п независимых испытаний (разыграно п возможных значений X) и по ним была найдена выборочная средняя
Интересующая нас верхняя граница ошибки δ есть не что иное, как «точность оценки» математического ожидания по выборочной средней при помощи доверительных интервалов, о которой уже шла речь в гл. XVI. Поэтому воспользуемся результатами, полученными ранее, и рассмотрим следующие три случая. 1. Случайная величина Х распределена нормально и ее среднее квадратическое отклонение σ известно. В этом случае с надежностью γ верхняя граница ошибки (см. гл. XVI, § 15)
где п— число испытаний (разыгранных значений X); t— значение аргумента функции Лапласа, при котором Ф (t) =γ/2, а—известное среднее квадратическое отклонение X. Пример 1. С надежностью γ =0,95 найти верхнюю границу ошибки σ, если для оценки математического ожидания нормальной величины Х с известным средним квадратическим отклонением, равным 0,5, было разыграно 100 возможных значений X. Решение. По условию, n =100, σ =0,5, Ф (t)= 0,95/2 =0,475. По таблице функции Лапласа (см. приложение 2) находим t =1,96. Искомая верхняя граница ошибки δ = 1,96·0,5/
2. Случайная величина Х распределена нормально, причем ее среднее квадратическое отклонение σ неизвестно. В этом случае с надежностью γ верхняя граница ошибки (см. гл. XVI, § 16)
где п— число испытаний; s —«исправленное» среднее квадратическое отклонение, tγ находят по таблице приложения 3. Пример 2. С надежностью γ =0,95 найти верхнюю границу ошибки δ, если для оценки математического ожидания нормальной величины Х было разыграно 100 ее возможных значений и по ним найдено «исправленное» среднее квадратическое отклонение s ==0,5. Решение. По условию, n =100, s =0,5. Используя таблицу приложения 3, по γ =0,95, n =100 находим tγ,=1,984. Искомая верхняя граница ошибки δ = 1,984·0,5/
3. Случайная величина Х распределена по закону, отличному от нормального. В этом случае при достаточно большом числе испытаний (n >30) с надежностью, приближенно равной γ, верхняя граница ошибки может быть вычислена по формуле (*), если среднее квадратическое отклонение σ случайной величины Х известно; если же σ неизвестно, то можно подставить в формулу (*) его оценку s— «исправленное» среднее квадратическое отклонение либо воспользоваться формулой (**). Заметим, что чем больше п, тем меньше различие между результатами, которые дают обе формулы. Это объясняется тем, что при п — Замечание. Для того чтобы найти наименьшее число испытаний, которые обеспечат наперед заданную верхнюю границу ошибки δ, надо выразить n из формул (*) и (**):
Например, если δ ==0,098, t =1,96, =0,5, то минимальное число испытаний, при которых ошибка не превысит 0,098, равно п= 1,9б2·0,52/0,0982=100. Случайные числа Ранее было указано, что метод Монте—Карло основан на применении случайных чисел; дадим определение этих чисел. Обозначим через R непрерывную случайную величину, распределенную равномерно в интервале (0, 1). Случайными числами называют возможные значения r непрерывной случайной величины R, распределенной равномерно в интервале (0, 1). В действительности пользуются не равномерно распределенной случайной величиной R, возможные значения которой, вообще говоря, имеют бесконечное число десятичных знаков, а квазиравномерной случайной величиной R*, возможные значения которой имеют конечное число знаков. В результате замены R на R* разыгрываемая величина имеет не точно, а приближенно заданное распределение. В приложении 9 приведена таблица случайных чисел, заимствованная из книги: БольшевЛ. Н., Смирнов Н. В. Таблицы математической статистики. М., «Наука», 1965, с. 428.
|
|||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 911; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.44.115 (0.01 с.) |

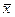 , которая принята в качестве искомой оценки: а*=х. Ясно, что если повторить опыт, то будут получены другие возможные значения X, следовательно, другая средняя, а значит, и другая оценка а*. Уже отсюда следует, что получить точную оценку математического ожидания невозможно. Естественно, возникает вопрос о величине допускаемой ошибки. Ограничимся отысканием лишь верхней границы δ допускаемой ошибки с заданной вероятностью (надежностью) γ:
, которая принята в качестве искомой оценки: а*=х. Ясно, что если повторить опыт, то будут получены другие возможные значения X, следовательно, другая средняя, а значит, и другая оценка а*. Уже отсюда следует, что получить точную оценку математического ожидания невозможно. Естественно, возникает вопрос о величине допускаемой ошибки. Ограничимся отысканием лишь верхней границы δ допускаемой ошибки с заданной вероятностью (надежностью) γ:
 (*)
(*) ==0,098.
==0,098.
 (**)
(**) распределение Стьюдента стремится к нормальному (см. гл. XVI, § 16, замечание). В частности (примеры 1 и 2), при n =100, γ =0,95 верхняя граница ошибки равна 0,098 по формуле (*) и 0,099 по формуле (**). Как видим, результаты различаются незначительно.
распределение Стьюдента стремится к нормальному (см. гл. XVI, § 16, замечание). В частности (примеры 1 и 2), при n =100, γ =0,95 верхняя граница ошибки равна 0,098 по формуле (*) и 0,099 по формуле (**). Как видим, результаты различаются незначительно.




