
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод произведений для вычисления выборочных средней и дисперсииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Метод произведений дает удобный способ вычисления условных моментов различных порядков вариационного ряда с равноотстоящими вариантами. Зная же условные моменты, нетрудно найти интересующие нас начальные и центральные эмпирические моменты. В частности, методом произведений удобно вычислять выборочную среднюю и выборочную дисперсию. Целесообразно пользоваться расчетной таблицей, которая составляется так: 1) в первый столбец таблицы записывают выборочные (первоначальные) варианты, располагая их в возрастающем порядке; 2) во второй столбец записывают частоты вариант; складывают все частоты и их сумму (объем выборки n) помещают в нижнюю клетку столбца; 3) в третий столбец записывают условные варианты ui = (xi - C) /h, причем в качестве ложного нуля С выбирают варианту, которая расположена примерно в середине вариационного ряда, и полагают h равным разности между любыми двумя соседними вариантами; практически же третий столбец заполняется так: в клетке строки, содержащей выбранный ложный нуль, пишут 0; в клетках над нулем пишут последовательно —1, —2, —3 и т.д., а под нулем—1, 2, 3 и т.д.; 4) умножают частоты на условные варианты и записывают их произведения niui - в четвертый столбец; сложив все полученные числа, их сумму 5) умножают частоты на квадраты условных вариант и записывают их произведения niui 2 в пятый столбец; сложив все полученные числа, их сумму 6) умножают частоты на квадраты условных вариант,увеличенных каждая на единицу, и записывают произведения ni (ui+ 1)2 в шестой контрольный столбец; сложив все полученные числа, их сумму Замечание 1. Целесообразно отдельно складывать отрицательные числа четвертого столбца (их сумму A 1записывают в клетку строки, содержащей ложный нуль) и отдельно положительные числа (их сумму A 2 записывают в предпоследнюю клеткустолбца); тогда Замечание 2. При вычислении произведений niui 2пятого столбца целесообразно числа niui четвертого столбца умножать на ui. Замечание 3. Шестой столбец служит для контроля вычислений: если сумма
После того как расчетная таблица заполнена и проверена правильность вычислений, вычисляют условные моменты:
Наконец, вычисляют выборочные среднюю и дисперсию по формулам (*) и (****) § 3:
Пример. Найти методом произведений выборочные среднюю и дисперсию следующего статистического распределения: варианты 10,2 10,4 10,6 10,8 11,0 11,2 11,4 11,6 11,8 12,0 частоты 2 3 8 13 25 20 12 10 6 1 Решение. Составим расчетную таблицу, для чего: 1) запишем варианты в первый столбец; 2) запишем частоты во второй столбец; сумму частот (100) поместим в нижнюю клетку столбца; 3) в качестве ложного нуля выберем варианту 11,0 (эта варианта расположена примерно в середине вариационного ряда); в клетке третьего столбца, которая принадлежит строке, содержащей выбранный ложный нуль, пишем 0; над нулем записываем последовательно—1, —2, —3, —4, а под нулем — 1, 2, 3, 4, 5; 4) произведения частот на условные варианты записываем в четвертый столбец; отдельно находим сумму (— 46) отрицательных и отдельно сумму (103) положительных чисел; сложив эти числа, их 5) произведения частот на квадраты условных вариант запишем в пятый столбец; сумму чисел столбца (383) помещаем в нижнюю клетку столбца; 6) произведения частот на квадраты условных вариант, увеличенных на единицу, запишем в шестой контрольный столбец; сумму (597) чисел столбца помещаем в нижнюю клетку столбца. В итоге получим расчетную табл. 7. Контроль:
Вычисления произведены правильно. Таблица 7
Вычислим условные моменты первого и второго порядков:
Найдем шаг: h = 10,4— 10,2 = 0,2. Вычислим искомые выборочные среднюю и дисперсию:
§ 5. Сведение первоначальных вариант к равноотстоящим
Выше изложена методика расчета выборочных характеристик для равноотстоящих вариант. На практике, как правило, данные наблюдений не являются равноотстоящими числами. Естественно, возникает вопрос: нельзя ли соответствующей обработкой наблюдаемых значений признака свести вычисления к случаю равноотстоящих вариант? Оказывается, можно. С этой целью интервал, в котором заключены все наблюдаемые значения признака (первоначальные варианты), делят на несколько равных частичных интервалов. (Практически в каждый частичный интервал должно попасть не менее 8—10 первоначальных вариант.) Затем находят середины частичных интервалов, которые и образуют последовательность равноотстоящих вариант.
В качестве частоты каждой «новой» варианты (середины частичного интервала) принимают общее число первоначальных вариант, попавших в соответствующий частичный интервал. Ясно, что замена первоначальных вариант серединами частичных интервалов сопровождается ошибками (первоначальные варианты левой половины частичного интервала будут увеличены, а варианты правой половины уменьшены), однако эти ошибки будут в основном погашаться, поскольку они имеют разные знаки. Пример. Выборочная совокупность объема п= 100 задана табл. 8. Составить распределение равноотстоящих вариант. Решение. Разобьем интервал 1,00—1,50, например, на следующие 5 частичных интервалов: 1,00—1,10; 1,10—1,20; 1,20—1,30; 1,30—1,40; 1,40—1,50. Таблица 8
Приняв середины частичных интервалов, в качестве новых вариант yi, получим равноотстоящие варианты: y 1=1,05; y 2=1,15; у 3 = 1,25; y 4=1.35; y 5 = 1,45. Найдем частоту варианты у 1 : n 1= 1+3 + 6 + 4+2 + 4/2= 18. (Поскольку первоначальная варианта 1,10 одновременно является концом первого частичного интервала и началом второго, частота 4 этой варианты поровну распределена между обоими частичными интервалами.) Найдем частоту варианты y 2: n 2 = 4/2 + 3 + 6 + 5 + 2 + 4/2 = 20. Аналогично вычислим частоты остальных вариант: n 3 = 25; п 4 = 22; n 5=15. В итоге получим следующее распределение равноотстоящих вариант: yi 1,05 1,15 1,25 1,35 1,45 ni 18 20 25 22 15 Рекомендуем читателю убедиться, что выборочные средние и дисперсии, вычисленные по первоначальным и равноотстоящим вариантам, окажутся соответственно равными:
Как видим, замена первоначальных вариант равноотстоящими не привела к существенным ошибкам; при этом объем вычислительной работы значительно уменьшается.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1678; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.105.195 (0.01 с.) |

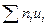 помещают в нижнюю клетку столбца;
помещают в нижнюю клетку столбца;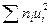 помещают в нижнюю клетку столбца;
помещают в нижнюю клетку столбца; помещают в нижнюю клетку столбца.
помещают в нижнюю клетку столбца.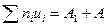 .
.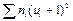 окажется равной сумме
окажется равной сумме  (как и должно быть в соответствии с тождеством
(как и должно быть в соответствии с тождеством 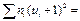
 )то вычисления проведены правильно.
)то вычисления проведены правильно.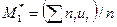 ,
, 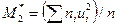 .
.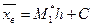 ,
, 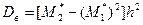 .
.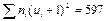 .
.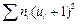 = 597
= 597
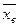 = 1,250;
= 1,250;  = 1,246; Dx = 0,018; Dy = 0,017.
= 1,246; Dx = 0,018; Dy = 0,017.


