
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выборочная дисперсия как оценка теоретической дисперсии, ско, «направленное» ско.Содержание книги
Поиск на нашем сайте
Пусть произведено n независимых испытаний, в результате которых величина Х приняла значения: х1, х2, …,хn. О: Выборочная дисперсия – это среднее арифметическое квадратов отклонения всех полученных значений от выборочного среднего.
или с учетом повторений
Из (2) следует,
Из (2) следует,
Поэтому выборочную дисперсию берут в качестве оценки теоретической дисперсии. Проверим на качество: 1)т.к. выборочн. средн явл-ся состоят. Оценкой мат. ожидания, то
M(X)
оценка состоятельная 2)Эта оценка является смещенной. Можно доказать, что
Чтобы избежать этого вводят исправленную выборочную дисперсию: S2=(n/(n-1))Dx*. Эта оценка является состоятельной т.к.
и несмещенной т.к.
В общем случае S2 не явл-ся эффективной оценкой, но м док-ть, что в общ случае норм распред-я она является асимптотически эффективной, т.е. при увеличении n ее дисперсия приближается к к минимально возможной. Исправ диспер польз при n<30, иначе дробь близка к 1 и S2 и Dx* практически совпадают. Для оценки СКО используется выборочное СКО:
и «исправленное» выборочное СКО:
Исправленным СКО является смещенная оценка, поэтому используют «». Доверительная вероятность и доверительный интервал. При больших n(n-число наблюдений) статистическая оценка неизвестного параметра q* близка к самому неизвестному параметру q, но если n мала, то оценка может значительно отличаться от оцениваемого параметра, возникает вопрос о степени доверия полученной оценки, т.е. о том, какова вероятность g того, что q* мало отличается от q, т.е. вероятность неравенства |q - q*|<d Очевидно, чем <d тем точнее оценка, поэтому d называют точностью оценки. Вероятность g, с которой осуществляется данное неравенство называют доверительной вероятностью (надежностью), а интервал [q*-d;q*+d] - доверительный интервал, он является интервальной оценкой параметра q. Для того, чтобы данное неравенство и его выполнение можно было считать почти достоверным, вероятность g обычно задают близко к 1. Точность d находят из условия:
Т.к. случайным здесь является не параметр q (вполне определенное, хотя и неизвестное число), а доверительный интервал (случайное его положение на оси) зависящий от q*, поэтому принято говорить не о попадании q в доверительный интервал, а говорят так: доверительный интервал включает в себя параметр q с надежностью g. Доверительный интервал для МО нормального распределения при известном и неизвестном s. Для известного. Пусть случ. величина Х имеет нормальное распределение и ее СКО (s) известно. Произведено n независимых испытаний по результатам которых вычислено Можно доказать, что если Х распределена нормально, то
Найдем доверительный интервал из условия
ранее для норм распред-я была получена формула
Применяя эту формулу для
где t находят по таблице ф-ции Лапласа, тогда
доверит интервал имеет вид:
Для неизвестного. Пусть величина X распределена нормально. Произведено n независимых испытаний в результате которых вычислены выборочные средние Рассмотрим вспомогательную случ. величину Известно, что T имеет так называемое распределение Стьюдента с (n-1) степенями свободы. Плотность вероятности этого распределения известна и обозначается f(t)=S(t,n). Распределение Стьюдента зависит только от числа n и не зависит от неизвестных параметров a и s, что является его достоинством. Найдем доверительный интервал из условия
преобразуем неравенство
тогда tg можно найти из условия: Созданы спецтаблицы, в которых по данным n и g находят tg=t(n,g),
доверительный интервал имеет вид:
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 405; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.210.196 (0.008 с.) |

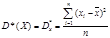 ,
,
 .
. аналогично формуле
аналогично формуле .
. стремится по вероятности к
стремится по вероятности к

 .
. ,
, .
.
 .
.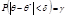
 являющееся оценкой неизвестного МО a. Нужно найти доверительный интервал покрывающий МО с вероятностью g. (рисунок)
являющееся оценкой неизвестного МО a. Нужно найти доверительный интервал покрывающий МО с вероятностью g. (рисунок)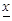 тоже распределена нормально. Доказывая несмещенность и эффективность
тоже распределена нормально. Доказывая несмещенность и эффективность  .
.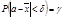 .
. .
. , получили
, получили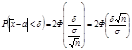
 ;
; ,
, ,
,
 .
. ,
, ,
, .
.
 ,
, .
.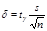 ,
, .
.


