
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие правила комбинаторики.Содержание книги
Поиск на нашем сайте
Общие правила комбинаторики. Правило суммы: если объект х может быть выбран n1 способами, а а у n2 способами, то объект “либо х либо у”, может быть выбран n1+ n2 способами. Правило произведения: если объект х может быть выбран n1 способами и каждый раз после этого объект у может быть выбран n2 способами, то объект “х и у”, (упорядоченная пара) может быть выбран n1 n2 Выборки без повторений (размещения, перестановки и сочетания) Размещениями ( без повторений ) из n элементов r называют упорядоченные выборки, имеющие r различных элементов выбранные из данных r элементов. Число всевозможных размещений обозначается: Перестановками называют выборки, сост. из всех n разл. эл-тов множества, отличающиеся друг от друга только порядком расположения. Обозначается: Pn=n! Перестановки - частный случай размещения, n=r. Сочетаниями (без повт.) из n по r называют выборки, имеющие r различных элементов, выбранные из данных n элементов. Случайные события и действия над ними. Событие, которое в результате опыта может произойти или не произойти называют случайным. Обозначают A, B, C, D… Выделяют 2 частных события: событие, которое в результате опыта обязательно наступит наз-ют достоверным. Событие, которое в результате опыта заведомо не произойдет наз-ют невозможным. Произведением А*В событий А и В наз-ют события, состоящие в появлении обоих событий. Суммой А+В наз-ют события, состоящие в появлении хотя бы одного из этих событий. Н-р: При бросании игральных костей А - выпадение четного числа очков, В - выпадение числа очков делящихся на три, то А*В=6, А+В=2,3,4,6. Событие Вероятность события. Статистическое определение вероятности. Мы часто сравниваем события, говоря что одно из них более вероятно, чем другое. В связи с этим, чтобы придать данному сравнению точный кон. смысл, требуется с каждым событием связать некоторое число, кот. выражало бы степень возможности события, т.е. было бы тем больше, чем более возможное событие. Это число мы назовем вероятностью. Вероятностью события наз-ся кол-ная мера степени объективной возможности данного события. Пусть произведено n испытаний, в результате которых событие А появилось m раз. Относительной частотой (частностью) события А наз-ся отношение числа m появления события к общему числу n всех испытаний Свойства вероятностей. 10 Вероятность любого события А удовлетворяет неравенству 0£P(A)£1. Док-во: 0£m£n; (: n) 0£(m\n)£1. 20 Вероятность достоверного события равно 1. Очевидно что все исходы благоприятствуют событию, т.е. m=n. 30 Вероятность невозможного события = 0. т. к. событие невозможно, ни один из исходов не благоприятствуют, т.е. m = 0. Условная вероятность. Теорема умножения вероятностей. Вероятность события А при условии что произошло событие В наз-ют условной вероятностью А при событии В и обозначают РB(A). Т еорема: вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность второго при условии, что произошло первое. Р(АВ)=Р(А)*РА(В) (1), Р(АВ)=Р(В)*РВ(А) (2). Док-во: Р(АВ)=к/n=m/n*k/m. m/n=P(A); k/m=PA(B), т.к. событие А произошло, то из всех возможных исходов остались только m благоприятных событию А, k из которых благоприятны событию В. Следствие: Р(А1А2…Аn)=Р(А1)*РА1(А2)*РА1А2(А3)*…*РА1А2…Аn-1(Аn). Формула полной вероятности. Пусть событие А может произойти с одним и только с одним из попарно несовместных событий В1, В2,…,Вn, образующих полную группу. Т.к. заранее не известно какое из событий Вi произойдет, то их наз-ют гипотезами, очевидно что наступление события А равносильно наступлению одного из попарно несовместных событий АВ1 или АВ2 или... АВn, т.е. А=АВ1+АВ2+…+АВn. По теореме сложения для несовместных событий имеем: Р(А)=Р(АВ1)+Р(АВ2)+…+Р(АВn), по теореме умножения имеем: Р(А)=Р(В1)*РВ1(А)+Р(В2)*РВ2(А)+…+Р(Вn)*РВn(А). P(A)=∑P(BK)*PBK(A) Формула Байеса. Пусть событие А может произойти с одним и только с одним из попарно несовместных событий гипотез В1,…,Bn образующих полную группу. Пусть известно, что произошло событие А. Этот факт может повлиять на вероятности гипотез, т. е. произойдет их переоценка. Найдем усл. вер-ть гипотез при условии что произошло событие А. Р(АВi)=Р(А)*РА(Вi)=Р(Вi)*РВi(А); РА(Вi)= Р(Вi)* РВi(А)/Р(А), или используя формулу полной вероятности:
Локальная теорема Лапласа. Если вероятность появления события А в каждом из n независимых испытаний постоянно и равна p (0<p<1), то вероятность появления события А в этих испытаниях m раз приближенно =
где
Для функции
составлены специальные таблицы при х из[0, 4), при x<0 пользуются четностью, при x>=4 полагают Теорема Пуассона. Ф-лу используют если p или d мало. Пусть для опред-ти мало p, и вер-ть появления события А удовлетвор. Условию np=λ-const, с такой ситуацией встреч при редких явлениях. Теорема: Пусть вероятность появления события А в серии из n независимых испыт. равна p=λ/n, тогда вер. появления события А в этой серии m раз удовл. условию:
(далее переписать эту формулу без предела). Ей пользуются при больших n и малых p и λ £10. Биноминальное распределен. Пусть вероятность появл. событ. А в каждом из n независимых испыт. = p. Рассмотрим случайную величину Х - число появления события А в этих испытаниях. Ее возможные значения i: 0, 1, 2, n. Их вероятность находят по формуле Бернулли. Распределение, описываемое данной формулой наз-ся биноминальным. П-р: составить закон распределения числа выпадений герба при шести бросаниях монеты. Неравенство Чебышева. Если испыт. много, то результат не зависит от случая, что позволяет предугадывать ход событий. Дан факт явл содерж з-на больших чисел, кот сост из ряда теорем, уст факт сущ-я сред хар-к больш числа величин некот конст-м. Лемма:(Нер Чебышева). Пусть случайная величина Х имеет конечное МО и конечную дисперсию, т.е M(Х) D(Х), тогда для любых e>0 справедливо Д-во: в неравенстве Чебышева речь идет о попадании случайной величины в e окрестность ее математического ожидания. Найдем вероятность противоположного события, т.е. P(|X-M(X)|³e) для дискретной случайной величины Х (для непрерывной величины д-во аналогично), только суммы заменяются соответствующими интегралами. Пусть возможное значение xi величины X имеет вероятность pi (i=1…n), обозначим xk1,xk2,…,xkm. Те значения величины Х для которых справедливо (|Xki-M(X)³e), i=1…n. Тогда Pk1+Pk2+…+Pkm=P(|X-M(X)|³e) по определению дисперсии имеем D(X)=(X1-M(X))2p1+(X2-M(X))2p2+…+(Xn-M(X))2pn ³ (Xk1-M(X))2pk1+(Xk2-M(X))2pk2+…+(Xkm-M(X))2pkm³ e2(pk1+pk2+…+pkm)=e2P(|X-M(X)|³e). P(|X-M(X)|³e)£D(X)/e2, тогда -p(|X-M(X)|³e)³- D(X)/e2, 1-P(|X-M(X)|³e)³1-D(X)/e2, т.е. p(|X-M(X)|<e)³1-D(X)/e2 Выборочное среднее. Пусть произведено n независимых испытаний, в результате которых величина Х приняла значения: х1, х2, …,хn. О: Выборочным средним наз-ют среднее ариф. всех полученных значений случайной величины.
Если значение xi имеют частоту ni и i=1,k,
то формула примет вид
Если распределение задано в интервальной форме, то в качестве xi выбирают середину i - того интервала. Преобразуем (2).
Выборочное среднее выбирают в качестве оценки МО случайной величины. Выборочное среднее является случайной величиной, меняющейся от выборки к выборке, причем значения x1, x2,…,xn можно рассматривать как возможные значения случайных величин: X1,X2,…Xn, являющихся «экземплярами» случайной величины X. Поэтому:
Проверим данную оценку на качество: 1) По частному случ. Т. Чеб.
Отсюда след.
2) 3) Можно доказать что если случайная величина имеет нормальное распределение то дисперсия выборочного среднего будет наименьшей, т.е. оценка будет эфективней. Общие правила комбинаторики. Правило суммы: если объект х может быть выбран n1 способами, а а у n2 способами, то объект “либо х либо у”, может быть выбран n1+ n2 способами. Правило произведения: если объект х может быть выбран n1 способами и каждый раз после этого объект у может быть выбран n2 способами, то объект “х и у”, (упорядоченная пара) может быть выбран n1 n2
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 192; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.157.241 (0.007 с.) |


 ;
;  ;
; 
 - наз-ют противоположным событию А, если оно состоит в не появления события А и А+
- наз-ют противоположным событию А, если оно состоит в не появления события А и А+  - достоверно. Для наглядности события изображают фигурами на плоскости, рассматривая событие как попадание случайно брошенной точки в соответствующую фигуру. Тогда событие А+В - это попадание в объединение фигур. А*В - это попадание в пересечение фигур.
- достоверно. Для наглядности события изображают фигурами на плоскости, рассматривая событие как попадание случайно брошенной точки в соответствующую фигуру. Тогда событие А+В - это попадание в объединение фигур. А*В - это попадание в пересечение фигур.  - попадание в дополнение.
- попадание в дополнение. Статистич. определение: при большом числе испытаний относительная частота большинства событий изменяется мало, колеблясь около некоторого постоянного числа р. Это число р и называют вероятностью события А. Н-р: При бросании монеты частота выпадения герба колеблется около Ѕ. Вероятность показывает как часто в среднем появляется событие А. Н-р: р=2/7 говорит о том, что при большом числе испытаний событие появляется в среднем в 2 случаях из 7.
Статистич. определение: при большом числе испытаний относительная частота большинства событий изменяется мало, колеблясь около некоторого постоянного числа р. Это число р и называют вероятностью события А. Н-р: При бросании монеты частота выпадения герба колеблется около Ѕ. Вероятность показывает как часто в среднем появляется событие А. Н-р: р=2/7 говорит о том, что при большом числе испытаний событие появляется в среднем в 2 случаях из 7.
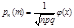


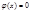 , т.к. функция быстро убывает. Ф-я четная. Формулой пользуются, если npq³10. Формула Лапласа дает более точный рез-т при р близких к 0,5, если p или q мало то погрешность м.б. большой. В этих случаях используют ф-лу Пуассона.
, т.к. функция быстро убывает. Ф-я четная. Формулой пользуются, если npq³10. Формула Лапласа дает более точный рез-т при р близких к 0,5, если p или q мало то погрешность м.б. большой. В этих случаях используют ф-лу Пуассона.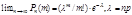

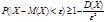
 .
. ,
,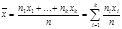 (2)
(2) .
. ,
, .
. .
. .
. (оцека не смещенная).
(оцека не смещенная). . При возрастании n D(X) убывает, но отсюда не следует её минимальность.
. При возрастании n D(X) убывает, но отсюда не следует её минимальность.


