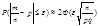Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегральная теорема Лапласа.Содержание книги
Поиск на нашем сайте
Пусть вероятность появления события А в каждом из n независимых испытаний постоянна и = р-const, тогда вероятность того, что в этих испытаниях события А появится не менее m1 и не более m2 раз приближенно =
где
Эти приближенные формулы будут тем точнее, чем больше число испытаний m, обычно ими пользуются когда npq³10. Функция Лапласа, ее свойства и график. Ф-я из интегральной теоремы Лапласа не интегрируется в конечном виде, поэт. вводят ф-ю:
(лучше писать русскую Ф) Свойства: 1) F(0)=0, 2) F(-x)=-F(x) 3) F(x) - монотонно возрастает, т.к.
- положит. ф-я. 4) lim (x®+¥)F(x)=1/2; lim (x®-¥)F(x)=-1/2. График: Для нее составлены таблицы при xÎ[0;5] F(5)=0,499995, при x>5 F(x) = 0,5, при x<0 пользуются ее нечетностью.
этой формулой пользуются при больших n и npq³10.
Применение интегральной теоремы Лапласа и функции Лапласа к вычислению вероятностей
Этой формулой пользуются при больших n и при npq=>10. Пусть производится n независ. испыт., в кажд из к-рых вер-ть появл. соб. А = p. Мы знаем, что при большом числе испыт. относит. частота соб. А близка к его вероятности. Найдем вер. того, что относит. частота отличается от вер-ти не более чем на Е³0, т.е.
-e£(m/n)-p£e; -e+p£(m/n)£e+p; np-ne£m£np+ne; (k1=np-ne, k2=np+ne); к1£m£k2.
Вычислим:
x’= - x’’;
18. Геометрическое определение вероятности. (без рисунка). Классич. опр-е вер-ти исп. в том случае, если имеется конечное число n всех элем. исходов. Если число исходов бесконечно, то используют геом. опр-е вероятности. Пусть плоская фигура G содержит фигуру g. На фиг. G случайным образом бросается точка, при этом предполагается, что вероятность ее попадания в любую часть фигуры G пропорц. площ. этой части и не завис. от ее расположения и формы. Тогда по определению полагают, что вероятность попадания точки в фигуру g равна p=Sg/SG, если G – прямая, то p=Lg/LG, если в пространстве, то V – объем, p=Vg/VG. Случайные величины. Закон распределения дискретной случайной величины. О: Случайной величиной наз-ся величина, которая в результате испытаний примет одно и только одно возможное значение, заранее неизвестное, какое именно. Случайная величина, множество значений которой конечно или счетно наз-ся дискретной. Случайная величина, множество значений которой есть некоторый промежуток наз-ся непрерывной. Случайные величины обозначаются большими буквами конца латинского алфавита, а их возможные значения - соответствующими маленькими буквами с индексами или без них.
Закон распределения: Пусть Х - дискретная случайная величина, принимающая значение х1,…,хn,…,(оно может быть конечным или счетным). Тот факт, что случайная величина Х примет значение хi, яв-ся случайным событием, которое обозначается X=хi, а вероятность этого события pi=P(X=хi). Законом распределения случайной величины наз-ся любое правило, устанав. зависимость м/у возможными значениями случайной величины и их вероятностями. Для дискретных случайных величин закон распределения записывается в виде таблицы, в первой строке которой возможные значения, а во второй соответствующая вероятность. (таблица) Т.к. в результате испытания величина Х обязательно примет одно и только одно из возможных значений, то событие X=х1, X=х2, …,X=хn,…, то событие образует полную группу попарно несовместных событий. Поэтому р1+…+рn+…=1 (это либо конечная сумма, либо сумма сходящегося ряда). Для наглядности закон распределения изображают графически. Для этого в прямоугольной системе координат отмечают точки с координатами (хi, pi) и соединяют их последовательно отрезками. Полученную ломанную наз-ют многоугольником распределения. Биноминальное распределен. Пусть вероятность появл. событ. А в каждом из n независимых испыт. = p. Рассмотрим случайную величину Х - число появления события А в этих испытаниях. Ее возможные значения i: 0, 1, 2, n. Их вероятность находят по формуле Бернулли. Распределение, описываемое данной формулой наз-ся биноминальным. П-р: составить закон распределения числа выпадений герба при шести бросаниях монеты.
|
|||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 321; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.35.234 (0.009 с.) |





 ;
;  ;
;  ,
, .
.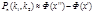

 ;
;  ;
;