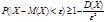Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плотность вер-ти и ее свойства. Связь с ф-ией распределения.Содержание книги
Поиск на нашем сайте Пусть дана непрерывная случ. величина Х, ф-я расп. к-рой F(x) имеет непр. производную. Опр: плотностью вероятности непрерывной случ. величины Х наз. производная ее функции распределения, т.е. f(x)=F/(x). Т: Вероятность того, что непр. случ. вел. примет значение, принадл. (a,b) определяется рав-вом:
Д-во:
Сл:
Д-во: Св-ва: 1) f(x)³0 т.к. f(x) – производная неотрицательная, т.к. F(x) – неубывающая ф-ия. 2) Доказательство:
геометрически это значит, что площадь всей фигуры, закл. м/у кривой распред-я и осью Ох=1
27. Нормальное распределение. Нормальная кривая. Вероятность попадания нормально распределенной случайной величины в интервалы Непрер-я случ. вел-на подчин-ся норм-у з-ну распр-я, если ее плотность вер-ти им. вид:
s>0 и a- пар-ры норм распред. График f(x) наз. нормальной кривой или кривой Гаусса. Для построения графика функции исследуем f(x). (6 пунктов самостоятельно). Найдем вероятность попадания нормально расп. сл. вел. в (a,b).
Частный случай: d=3s P(|X-a|<3s)=2Ф(3)=0.99 Т.к. вероятность близка к 1, то можно считать практически достоверным, что нормально распределенная случ. величина не выходит за пределы интервала (a-3s,a+3s). Это “правило трех сигм”. Числовые хар-ки непрерывной случайной величины. 1. МО. Пусть случ велич-на имеет возможные значен-я X: x1,…,xn с соответствующими вер-ми p1,…,pn. О: МО случ. вел. – это сумма произведен. всех ее возм. знач-й на их вероятность. Если конечное число значений, то М(Х)=х1*р1+…+ хn*рn. Если мн-во знач-й счетно, то М(Х)=åxipi, причем этот рад сход-ся абсолютно, чтобы его сумма не зависела от порядка расположения членов. Пусть непрерывная случайная величина задана плотностью вероятности f(x). О: МО непрер. случ. велич. – интеграл.
Несобственный интеграл должен сход. абсолютно. Вероятностный смысл: МО прибл. равно среднему арифмет. наблюдаемых знач-й. случ. велич.(тем точнее, чем больше число испытаний).
2. Дисперсия сл. величины – это МО квадрата отклонения случайной величины от ее МО. D(Х)=М[X-M(X)]2
На практике пользуются другой формулой: D(X)=M[x2-2X*M(X)+(M(X))2] = M(X2)-M(2X*M(X))+M[(M(X))2] = M(X2)-2M(X)*M(X)+(M(X))2 = M(X2)-[M(X)]2.
Свойства: 10 D(с)=0. с- const; док-тво: D(с)=М(с2)-М2(с)=с2-с2=0 20 D(сХ)=с2D(Х) 30 D(Х+Y)=Д(X+Y), если x,y - независимы. Следствие: D(Х-Y)=D(X+Y)
3. СКО Дисперсия имеет недостаток, она имеет размерность квадрата случ. величины. Поэтому с учетом того, что D(x)³0, вводят другую характеристику: СКО. О: СКО – это квадратный корень из её дисперсии. D(Х)=M(X2)-M2(X).
Свойство СКО. 10 s(с)=0, с - const; 20 s(сX)=|c|s(X). Математическое ожидание и дисперсия нормального распределения. Плотность нормального распределения
Можно доказать, что М(Х)=а, а Д(Х)=s2 и s(Х)= s. Итак, параметры а и s нормального распределения равны соответственно МО и СКО. Пример: случ. величина Х распределена по нормальному закону. МО и СКО этой вел = 30, 10. Найти: вероятность того, что 1) Х прин (10,50) 2) отклонение по абс. величине будет меньше 3. a=30-b, s=10-a; P(a<X<b)=Ф(b-a/s)- Ф(a-a/s); 1) P(10<X<50)=Ф(2)-Ф(-2)=2Ф(2)=0.95. 2) P(|x-a|<d)=2Ф(d/s), P(|X-30|<3)=2Ф(0.3)=0.2358. Неравенство Чебышева. Если испыт. много, то результат не зависит от случая, что позволяет предугадывать ход событий. Дан факт явл содерж з-на больших чисел, кот сост из ряда теорем, уст факт сущ-я сред хар-к больш числа величин некот конст-м. Лемма:(Нер Чебышева). Пусть случайная величина Х имеет конечное МО и конечную дисперсию, т.е M(Х) D(Х), тогда для любых e>0 справедливо Д-во: в неравенстве Чебышева речь идет о попадании случайной величины в e окрестность ее математического ожидания. Найдем вероятность противоположного события, т.е. P(|X-M(X)|³e) для дискретной случайной величины Х (для непрерывной величины д-во аналогично), только суммы заменяются соответствующими интегралами. Пусть возможное значение xi величины X имеет вероятность pi (i=1…n), обозначим xk1,xk2,…,xkm. Те значения величины Х для которых справедливо (|Xki-M(X)³e), i=1…n. Тогда Pk1+Pk2+…+Pkm=P(|X-M(X)|³e) по определению дисперсии имеем D(X)=(X1-M(X))2p1+(X2-M(X))2p2+…+(Xn-M(X))2pn ³ (Xk1-M(X))2pk1+(Xk2-M(X))2pk2+…+(Xkm-M(X))2pkm³ e2(pk1+pk2+…+pkm)=e2P(|X-M(X)|³e). P(|X-M(X)|³e)£D(X)/e2, тогда -p(|X-M(X)|³e)³- D(X)/e2, 1-P(|X-M(X)|³e)³1-D(X)/e2, т.е. p(|X-M(X)|<e)³1-D(X)/e2
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 329; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |


 . График плотности вер-ти наз. кривой распределения. Вер. попадания сл. вел. в интервал (a,b)=площ. фигуры, ограниченной кривой распределения, осью Ох и прямыми х=a, х=b. Плотность вер-ти показ-ет как часто случ вел-на попадает в окр-ть точки при повтор-и опыта.
. График плотности вер-ти наз. кривой распределения. Вер. попадания сл. вел. в интервал (a,b)=площ. фигуры, ограниченной кривой распределения, осью Ох и прямыми х=a, х=b. Плотность вер-ти показ-ет как часто случ вел-на попадает в окр-ть точки при повтор-и опыта.



 и
и 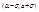 . Правило трех сигм.
. Правило трех сигм. ,
,
 .
.

 .
.