
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интервальная оценка математического ожидания нормального распределения при неизвестной дисперсииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В том случае, когда исследуемый признак имеет нормальное распределение с неизвестным математическим ожиданием а и неизвестной дисперсией В данном случае поступают следующим образом. По данным выборки строят случайную величину Т:
которая имеет распределение Стьюдента с k = n – 1 степенями свободы; здесь Плотность распределения Стьюдента
где Распределение Стьюдента определяется единственным параметром n – объемом выборки и не зависит от неизвестных параметров а и
Заменив неравенство
Последнее равенство представляет собой соотношение для доверительного интервала
Задача. Получено следующее распределение 100 рабочих цеха по выработке в отчетном году (в % к предыдущему году):
Предположим, что выработка на одного рабочего в отчетном году (в % к предыдущему) подчиняется нормальному закону распределения. Построить доверительный интервал надежности 0,95 для средней выработки на одного рабочего. Решение. Можно показать, что выборочные характеристики данного распределения таковы:
которое будет использоваться нами для решения поставленной задачи. Пользуясь таблицей значений
Таким образом, с надежностью 0,95 неизвестный параметр а заключен в доверительном интервале
Контрольные вопросы
1. В чем состоит разница в понятиях: точечная оценка параметра и интервальная оценка параметра? 2. Какая из оценок является более точной: точечная или интервальная? 3. Что называют доверительной вероятностью? 4. Что называют точностью оценки? 5. Влияет ли выбор доверительной вероятности на: а) точечную оценку; б) интервальную оценку?
6. Как изменится доверительный интервал для параметра распределения, если увеличить доверительную вероятность? 7. Как строится доверительный интервал для оценки математического ожидания нормально распределенного признака, если: а) теоретическая дисперсия известна; б) теоретическая дисперсия неизвестна?
Контрольные задания
1. Для настройки технологической линии электролампового завода произведена случайная выборка в количестве 100 ламп из дневной выработки завода. Средняя продолжительность горения ламп в выборке составила 350 часов. Предполагая, что продолжительность горения лампочки является нормально распределенной случайной величиной со средним квадратическим отклонением 24 часа, с надежностью 0,95 найти доверительный интервал для средней продолжительности горения лампочки во всей дневной выработке завода. 2. Службой контроля проверен расход электроэнергии в течение месяца в 10 наудачу выбранных квартирах многоквартирного дома, в результате чего были получены следующие значения (кВт/ч): 125, 86, 104, 140, 90, 55, 125, 98, 64, 102. Предположим, что расход электроэнергии является нормально распределенной случайной величиной со средним квадратическим отклонением, равным 10 кВт/ч. С надежностью 0,95 необходимо построить доверительный интервал для оценки среднего расхода электроэнергии в доме. 3. Та же задача при условии, что среднее квадратическое отклонение расхода электроэнергии неизвестно.
Литература 1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2002. – Гл. 16, п.п. 1 – 20.
3. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1999. – Гл. 14.
Статистические гипотезы
На разных стадиях экономико-статистического исследования часто возникает необходимость формулировки, а затем экспериментальной проверки некоторых предположений или гипотез. Например, при контроле качества продукции во многих ситуациях предполагается, что измеряемые величины нормально распределены вокруг их номинального значения или что применение нового прибора, устройства и т.д. существенно повышает производительность труда. Задача состоит в том, чтобы проверить, не противоречит ли высказанное предположение имеющимся результатам наблюдений.
Понятие «статистическая гипотеза» означает любое предположение о виде или свойствах распределения генеральной совокупности, из которой извлечена выборка. Такие предположения можно делать на основании теоретических соображений или других статистических исследований. Пусть, например, многократно измеряется некоторая физическая величина, точное значение а которой не известно и в процессе измерений не меняется. На результаты измерений влияют многие случайные факторы: точность настройки измерительного прибора, погрешность округления при считывании данных и т.п. Поэтому результат i -го измерения Статистическая гипотеза, являющаяся утверждением о параметрах генеральной совокупности называется параметрической. Гипотеза, содержащая утверждение обо всем распределении изучаемого признака называется непараметрической. Различают также простую и сложную гипотезы. Гипотеза называется простой, если она однозначно определяет распределение исследуемого признака; в противном случае гипотеза называется сложной. Например, простой параметрической гипотезой является утверждение о том, что изучаемый признак Х имеет стандартное нормальное распределение. Если же высказывается предположение, что наблюдаемый признак Х имеет нормальное распределение, не указывая при этом конкретное значение среднего и дисперсии или указывая значение только одного параметра, то это сложная гипотеза. Процедура обоснования сопоставления высказанной статистической гипотезы с имеющимися в нашем распоряжении выборочными данными называется проверкой статистической гипотезы. Результат подобного сопоставления может быть либо отрицательным, либо неотрицательным. В первом случае данные наблюдения противоречат высказанной гипотезе, а потому от этой гипотезы следует отказаться, во втором – данные наблюдений не противоречат высказанной гипотезе, следовательно, ее можно принять в качестве одного из допустимых предположений. При этом неотрицательный результат проверки гипотезы не означает, что высказанное нами предположение является единственно верным, – просто оно не противоречит имеющимся выборочным данным. Однако таким же свойством наряду с проверяемой гипотезой могут обладать и другие гипотезы. Так что даже статистически проверенное предположение следует расценивать не как раз и навсегда установленный факт, а как достаточно правдоподобное, не противоречащее имеющимся данным утверждение. Проверяемая гипотеза называется основной или нулевой и обозначается
Например, рассмотрим нулевую гипотезу Проверка статистических гипотез на основании выборочных данных неизбежно связана с риском принятия ложного решения. При этом возможны два ошибочных решения: · отклонение верной нулевой гипотезы – ошибка 1-го рода; вероятность ошибки 1-го рода принято обозначать · принятие неверной нулевой гипотезы – ошибка 2-го рода; вероятность ошибки 2-го рода принято обозначать Возможные результаты статистической проверки представлены ниже в таблице:
Последствия указанных ошибок часто оказываются различными. Например, если основная гипотеза состоит в признании продукции предприятия качественной и допущена ошибка 1-го рода, то будет забракована годная продукция. Допустив ошибку 2-го рода, производитель отправляет потребителю брак. В данном случае последствия второй ошибки более серьезны с точки зрения имиджа фирмы и ее долгосрочных перспектив. Если основная гипотеза состоит в наличии некоторого заболевания у пациента, то ошибка 2-го рода приведет к неправильному заключению о необходимости лечения. В результате ошибки 1-го рода имеющееся заболевание не будет обнаружено, что может привести к летальному исходу. Исключить ошибки первого и второго рода во многих случаях невозможно в силу ограниченности выборки. Поэтому стремятся минимизировать потери от этих ошибок. Одновременное уменьшение вероятностей данных ошибок при фиксированном объеме выборки невозможно, так как задачи их уменьшения являются конкурирующими, и снижение вероятности допустить одну из них влечет за собой увеличение вероятности допустить другую. В большинстве случаев единственный способ уменьшения вероятности ошибок состоит в увеличении объема выборки.
Критерии проверки гипотез Для выбора между основной гипотезой Н0 и альтернативной Н1 необходимо действовать по какому-либо правилу. Статистически критерием или критерием называется случайная величина К, использующаяся для проверки статистической гипотезы.
Построение большинства критериев проверки основной гипотезы против альтернативной осуществляется следующим образом. Вначале пытаются найти функцию После того, как критерий К выбран, множество всех его возможных значений оказывается разбитым на два непересекающихся подмножества. В одном из них содержатся те значения К, при которых нулевая гипотеза Н0 принимается, а во втором – те значения критерия К, при которых нулевая гипотеза Н0 отвергается. Первое подмножество называется областью принятия гипотезы, а второе – критической областью. Критическая область и область принятия гипотезы – интервалы, точки которые их разделяют, называются критическими точками. Различные типы критических областей представлены ниже в таблице, здесь же приведены требования, согласно которым определяются критические точки тех или иных критических областей. При этом важно помнить, что критическая точка определяется после того, как задана малая вероятность – уровень значимости
Схему проверки статистических гипотез можно описать следующим образом. 1. Выдвигается нулевая гипотеза Н0 и альтернативная гипотеза Н1; 2. Задается уровень значимости 3. Выбирается статистика критерия К; 4. Определяется распределение статистики критерия К при условии, что верна гипотеза Н0. 5. Исходя из распределения статистики К в условиях справедливости гипотезы Н0 и формулировки альтернативной гипотезы Н1 определяется критическая область методом, описанным в таблице выше; 6. По имеющимся данным наблюдений вычисляется значение Кнабл статистики критерия К; 7. Принимается статистическое решение: · если выборочное значение Кнабл статистики критерия К принадлежит критической области, то нулевую гипотезу Н0 нужно отклонить как не согласующуюся с результатами наблюдений; · если выборочное значение Кнабл статистики критерия К не принадлежит критической области, а значит принадлежит области принятия гипотезы, то нулевую гипотезу Н0 нужно принять, т.е. считать, что гипотеза Н0 не противоречит результатам наблюдений.
Контрольные вопросы
1. Сформулируйте определение понятия статистическая гипотеза.
2. Какие выводы делаются при проверке статистических гипотез? 3. Какую гипотезу называют: а) нулевой; б) конкурирующей; в) параметрической; г) простой; д) сложной? 4. Определите понятие ошибок 1-го рода и 2-города. 5. Можно ли одновременно уменьшить вероятности ошибок 1-го и 2-го рода? 6. Что называется статистическим критерием? 7. Что называется критической областью? 8. Что называется областью принятия гипотезы? 9. Дайте определение: а) правосторонней критической области; б) левосторонней критической области; в) двусторонней критической области. 10. Как определяются критические точки: а) правосторонней критической области; б) левосторонней критической области; в) двусторонней критической области? 11. В чем состоит схема проверки статистических гипотез?
Контрольные задания
1. Наблюдаемый объект может быть либо своим, либо объектом противника. Система обнаружения относит объект к одному из классов по результатам нескольких замеров определенных характеристик. Сформулируйте нулевую и альтернативную гипотезы, если в результате ошибки 1-го рода происходит пропуск цели. В чем состоит ошибка 2-го рода? 2. Если
43.Критерий согласия Пирсона «Хи-квадрат» ( На практике часто возникают задачи, связанные с тем, что вид закона распределения исследуемого признака – гипотетический и подлежит проверке. Если проводить графическое сравнение полигона или гистограммы частот с кривой распределения, то можно получить представление, по крайней мере с качественной стороны, о большей или меньшей близости теоретического и эмпирического распределений. Предположим, что выборка Существуют различные критерии согласия, например, критерий согласия Пирсона Предположим, что проверяется основная гипотеза Н0: исследуемый признак Х имеет распределение Проверка нулевой гипотезы Н0 против альтернативной 1. Исходя из выборочных данных, находят оценки 2. Вся область изменения признака Х разбивается на k непересекающихся интервалов
3. Находятся теоретические вероятности
Если исследуемый признак дискретный, то
где суммирование ведется по всем значениям индекса r, для которых Очевидно, должно выполняться равенство 4. Вычисляется мера расхождения между теоретическим и эмпирическим распределением:
где 10. Для выбранного уровня значимости 11. Производится сравнение вычисленного по выборке значения
Задача. Получено следующее распределение 100 рабочих цеха по выработке в отчетном году (в % к предыдущему году):
С помощью критерия согласия Пирсона Решение. Нулевая гипотеза Н0 состоит в том, что исследуемый признак Х – выработка на одного рабочего в отчетном году (в % к предыдущему) подчиняется нормальному закону распределения. В качестве оценок двух неизвестных параметров а и Теоретические вероятности
Необходимые для этих вычислений значения функции
Вычисленное статистическое значение критерия
Контрольные вопросы
9. Что называется критерием согласия? 10. Сформулируйте схему применения критерия согласия «хи-квадрат» Пирсона.
Контрольные задания
7. Автомат наполняет ампулы лекарственным раствором. Контрольная проверка по схеме собственно случайной бесповторной выборки сотни ампул дала следующее распределение в них лекарств:
Используя критерий согласия Пирсона «хи-квадрат» при уровне значимости 8. В цехе с 10 станками ежедневно регистрировалось число вышедших из строя станков. Всего было произведено 200 наблюдений, результаты которых приведены ниже:
При уровне значимости Литература 1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2002. – Гл. 19, п.п. 1 – 14, 23. 2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2002. – Гл. 13, п.п. 1 – 6, 16.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1259; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.27.154 (0.011 с.) |

 , невозможно воспользоваться результатами п. 40.1, в котором дисперсия предполагалась известной.
, невозможно воспользоваться результатами п. 40.1, в котором дисперсия предполагалась известной.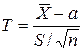 ,
,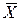 – выборочная средняя; S – исправленное среднее квадратическое отклонение; n – объем выборки.
– выборочная средняя; S – исправленное среднее квадратическое отклонение; n – объем выборки.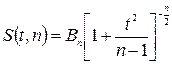 ,
,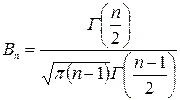 .
.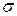 .
. 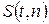 является четной функцией от t, вероятность осуществления неравенства
является четной функцией от t, вероятность осуществления неравенства 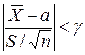 определяется так:
определяется так: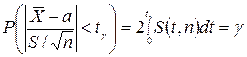 .
.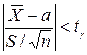 равносильным ему двойным неравенством, получим
равносильным ему двойным неравенством, получим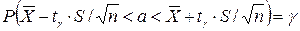 .
.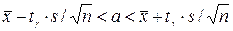 , покрывающий неизвестный параметр а с надежностью
, покрывающий неизвестный параметр а с надежностью 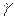 . Здесь
. Здесь  и s – выборочные значения признака.
и s – выборочные значения признака.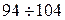
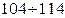
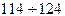
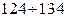
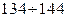
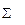
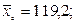
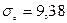 . С учетом того, что
. С учетом того, что 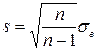 , получим соотношение
, получим соотношение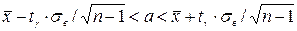 ,
,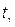 по
по 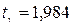 . Найдем границы доверительного интервала:
. Найдем границы доверительного интервала: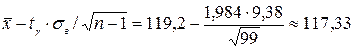 ,
,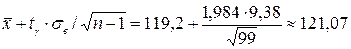 .
.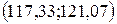 .
.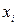 можно записать в виде
можно записать в виде 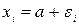 , где
, где 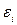 - случайная погрешность измерения. Обычно считают, что общая ошибка
- случайная погрешность измерения. Обычно считают, что общая ошибка 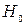 . Гипотеза, которая противопоставляется нулевой, называется альтернативной или конкурирующей и обозначается
. Гипотеза, которая противопоставляется нулевой, называется альтернативной или конкурирующей и обозначается 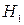 . В качестве конкурирующей часто выступает гипотеза, противоположная основной. Кроме того, альтернативных гипотез может быть несколько или бесконечно много.
. В качестве конкурирующей часто выступает гипотеза, противоположная основной. Кроме того, альтернативных гипотез может быть несколько или бесконечно много.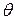 принимает значение, равное
принимает значение, равное 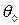 , т.е.
, т.е. 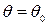 . В качестве альтернативной можно рассмотреть одну из следующих гипотез: а)
. В качестве альтернативной можно рассмотреть одну из следующих гипотез: а) 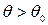 ; б)
; б) 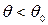 ; в)
; в) 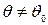 .
. , т.е.
, т.е. 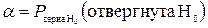 ;
; 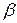 , т.е.
, т.е. 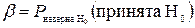 .
. от выборочных данных (т.е. статистику), которая характеризовала бы отклонение выборочных данных от гипотетических значений исследуемого признака, соответствующих гипотезе Н0. При этом статистика К должна быть такой, чтобы ее распределение в случае справедливости Н0 можно было бы определить точно или приближенно. Такая статистика называется статистикой критерия.
от выборочных данных (т.е. статистику), которая характеризовала бы отклонение выборочных данных от гипотетических значений исследуемого признака, соответствующих гипотезе Н0. При этом статистика К должна быть такой, чтобы ее распределение в случае справедливости Н0 можно было бы определить точно или приближенно. Такая статистика называется статистикой критерия.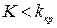 , где
, где 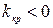
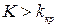 , где
, где 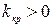
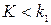 и
и  , где
, где 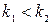

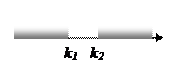
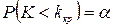
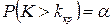
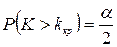 , где
, где 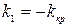 ,
, 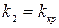
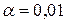 и
и 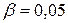 , то какие ошибки и как часто будем совершать в результате статистической проверки гипотезы?
, то какие ошибки и как часто будем совершать в результате статистической проверки гипотезы?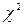 )
)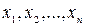 извлечена из генеральной совокупности с неизвестной теоретической функцией распределения
извлечена из генеральной совокупности с неизвестной теоретической функцией распределения 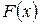 , относительно которой имеются две непараметрические гипотезы: простая основная Н0:
, относительно которой имеются две непараметрические гипотезы: простая основная Н0: 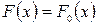 и сложная конкурирующая Н1:
и сложная конкурирующая Н1: 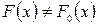 , где
, где 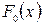 - известная функция распределения. Иными словами, мы хотим проверить, согласуются ли исходные данные с нашим гипотетическим предположением относительно теоретического закона распределения или нет. Поэтому критерий для проверки гипотез Н0 и Н1 называются критериями согласия.
- известная функция распределения. Иными словами, мы хотим проверить, согласуются ли исходные данные с нашим гипотетическим предположением относительно теоретического закона распределения или нет. Поэтому критерий для проверки гипотез Н0 и Н1 называются критериями согласия.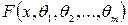 , против конкурирующей противоположной гипотезы
, против конкурирующей противоположной гипотезы 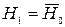 при уровне значимости
при уровне значимости 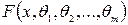 - функция распределения исследуемого при з нака Х, известная с точностью до параметров
- функция распределения исследуемого при з нака Х, известная с точностью до параметров 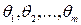 . В силу взаимно однозначного соответствия между функцией распределения и рядом (плотностью) распределения нулевая гипотеза Н0 может быть сформулирована также в терминах ряда (плотности) распределения. Если основная гипотеза простая, т.е. гипотетическое распределение исследуемого признака основной гипотезой определяется однозначно, то количество параметров распределений, требуемых оценки по выборке, m = 0.
. В силу взаимно однозначного соответствия между функцией распределения и рядом (плотностью) распределения нулевая гипотеза Н0 может быть сформулирована также в терминах ряда (плотности) распределения. Если основная гипотеза простая, т.е. гипотетическое распределение исследуемого признака основной гипотезой определяется однозначно, то количество параметров распределений, требуемых оценки по выборке, m = 0.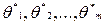 неизвестных параметров распределения
неизвестных параметров распределения 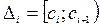 при i = 1, 2, …, k. Если признак Х принимает значения на всей вещественной оси, то полагаем
при i = 1, 2, …, k. Если признак Х принимает значения на всей вещественной оси, то полагаем 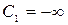 и правый конец
и правый конец 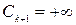 . Если признак Х принимает только положительные значения, то полагаем
. Если признак Х принимает только положительные значения, то полагаем 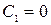 и правый конец
и правый конец 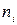 - количество выборочных данных, попавших в i -тый интервал
- количество выборочных данных, попавших в i -тый интервал 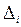 при i = 1, 2, …, k. Интервалы
при i = 1, 2, …, k. Интервалы 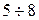 . Очевидно,
. Очевидно,  − объем выборки.
− объем выборки.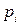 того, что исследуемый признак Х примет какое–либо значение из промежутка
того, что исследуемый признак Х примет какое–либо значение из промежутка 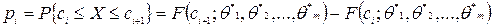 , i = 1, 2, …, k.
, i = 1, 2, …, k.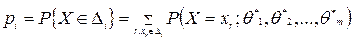 ,
,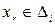 , i = 1, 2, …, k.
, i = 1, 2, …, k.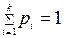 .
.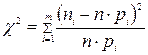 ,
,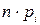 - теоретические частоты,
- теоретические частоты, 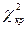 при числе степеней свободы
при числе степеней свободы 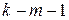 , где k – число выборочных групп, m - число параметров теоретического распределения, определяемого по опытным данным.
, где k – число выборочных групп, m - число параметров теоретического распределения, определяемого по опытным данным.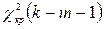 . Если значения
. Если значения 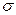 будут фигурировать соответствующие выборочные характеристики:
будут фигурировать соответствующие выборочные характеристики: 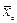 и
и 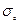 . Можно показать, что
. Можно показать, что 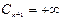 .
.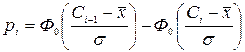 , i = 1, 2, …, k.
, i = 1, 2, …, k.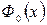 взяты из таблицы Приложения. Дальнейшие выкладки сведены ниже в таблицу. При этом объединены два последних интервала группировки ввиду их малочисленности.
взяты из таблицы Приложения. Дальнейшие выкладки сведены ниже в таблицу. При этом объединены два последних интервала группировки ввиду их малочисленности.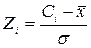
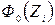
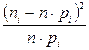
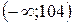
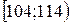
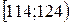
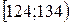
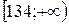

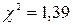
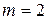 найдем число степеней свободы 5 – 3 = 2. Для заданного уровня значимости критерия
найдем число степеней свободы 5 – 3 = 2. Для заданного уровня значимости критерия  и числа степеней свободы, равного 2, находим
и числа степеней свободы, равного 2, находим 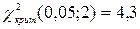 . Так как
. Так как 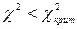 , то нулевая гипотеза о нормальности распределения величины выработки рабочего согласуется с имеющимися данными.
, то нулевая гипотеза о нормальности распределения величины выработки рабочего согласуется с имеющимися данными.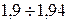

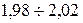
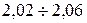
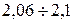
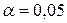 , проверить гипотезу о том, что случайная величин Х – объем лекарства в ампуле распределена по нормальному закону.
, проверить гипотезу о том, что случайная величин Х – объем лекарства в ампуле распределена по нормальному закону.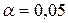 проверить гипотезу о том, что число выбывших из строя станков имеет распределение Пуассона.
проверить гипотезу о том, что число выбывших из строя станков имеет распределение Пуассона.


