
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическое определение вероятностиСодержание книги
Поиск на нашем сайте
Как было сказано выше, классическое определение вероятности предполагает, что все элементарные исходы равновозможны. О равновозможности исходов опыта заключают в силу соображений симметрии. Задачи, в которых можно исходить из соображений симметрии, на практике встречаются редко. Во многих случаях трудно указать основания, позволяющие считать, что все элементарные исходы равновозможны. В связи в этим появилась необходимость введения еще одного определения вероятности, называемого статистическим. Предварительно введем понятие относительной частоты. Относительной частотой события, или частотой, называется отношение числа опытов, в которых появилось это событие, к числу всех произведенных опытов. Обозначим частоту события А через W(A), тогда
где n – общее число опытов; m – число опытов, в которых появилось событие А. При небольшом числе опытов частота события носит в значительной мере случайный характер и может заметно меняться от одной группы опытов к другой. Например, при каких-то десяти бросаниях монеты вполне возможно, что герб появится 2 раза (частота 0,2), при других десяти бросаниях мы вполне можем получить 8 гербов (частота 0,8). Однако при увеличении числа опытов частота события все более теряет свой случайный характер; случайные обстоятельства, свойственные каждому отдельному опыту, в массе взаимно погашаются, и частота проявляет тенденцию стабилизироваться, приближаясь с незначительными колебаниями к некоторой средней постоянной величине. Эту постоянную, являющуюся объективной числовой характеристикой явления, считают вероятностью данного события. Статистическое определение вероятности: вероятностью события называют число, около которого группируются значения частоты данного события в различных сериях большого числа испытаний. Свойство устойчивости частот, многократно проверенное экспериментально и подтверждающееся опытом человечества, есть одна из наиболее характерных закономерностей, наблюдаемых в случайных явлениях. Между частотой события и его вероятностью существует глубокая связь, которую можно выразить так: когда мы оцениваем степень возможности какого-либо события, мы связываем эту оценку с большей или меньшей частотой появления аналогичных событий на практике.
Геометрическая вероятность
Допустим, что на плоскости задана квадрируемая область G, т.е. область, имеющая площадь SG. В области G содержится область g площади Sg. В область G наудачу брошена точка. Будем считать, что брошенная точка может попасть в некоторую часть области G с вероятностью, пропорциональной площади этой части и независящей от ее формы и расположения. Пусть событие А – «попадание брошенной точки в область g», тогда геометрическая вероятность этого события определяется формулой:
В общем случае понятие геометрической вероятности вводится следующим образом. Обозначим меру области g (длину, площадь, объем) через mes g, а меру области G – через mes G; пусть также А – событие «попадание брошенной точки в область g, которая содержится в области G». Вероятность попадания в область g точки, брошенной в область G, определяется формулой
Задача. В круг вписан квадрат. В круг наудачу бросается точка. Какова вероятность того, что точка попадёт в квадрат? Решение. Пусть радиус круга равен R, тогда площадь круга равна Контрольные вопросы
1. Что называется испытанием (опытом)? 2. Что называется событием? 3. Какое событие называется а) достоверным? б) случайным? в) невозможным? 4. Какие события называются а) несовместными? б) совместными? 5. Какие события называются противоположными?ываются а) несовместными б) совместнымиывается случайным? 6. Что называется полной группой случайных событий? 7. Если события
8. Образуют ли события А и 9. Какие элементарные исходы благоприятствуют данному событию? 10. Какое определение вероятности называется классическим? 11. В каких пределах заключена вероятность любого события? 12. При каких условиях применяется классическая вероятность? 13. При каких условиях применяется геометрическая вероятность? 14. Какое определение вероятности называется геометрическим? 15. Что называется частотой события? 16. Какое определение вероятности называется статистическим?
Контрольные задания
1. Из букв слова «консерватория» наугад извлекается одна буква. Найти вероятность того, что эта буква гласная. Найти вероятность, что это буква «о». 2. На одинаковых карточках написаны буквы «о», «р», «с», «т». Найти вероятность того, что на разложенных наудачу в ряд карточках появится слово «трос». 3. В бригаде 4 женщины и 3 мужчины. Среди членов бригады разыгрывается 4 билета в театр. Какова вероятность того, что среди обладателей билетов окажется 2 женщины и 2 мужчины? 4. Подбрасывается два игральных кубика. Найти вероятность того, что сумма очков на обоих кубиках больше 6. 5. На пяти одинаковых карточках написаны буквы л, м, о, о, т. Какова вероятность того, что извлекая карточки по одной наугад, получим в порядке их выхода слово «молот»? 6. Из 10 билетов выигрышными являются 2. Чему равна вероятность того, что среди взятых наудачу пяти билетов один выигрышный? 7. Какова вероятность того, что в наудачу выбранном двузначном числе цифры таковы, что их произведение равно нулю. 8. Наудачу выбрано число, не превосходящее 30. Найти вероятность того, что это число является делителем 30. 9. Наудачу выбрано число, не превосходящее 30. Найти вероятность того, что это число кратно 3. 10. Наудачу выбрано число, не превосходящее 50. Найти вероятность того, что это число простое.
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 379; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.34.148 (0.009 с.) |

 ,
, Классическое определение вероятности предполагает, что число элементарных исходов конечно. На практике встречаются опыты, для которых множество таких исходов бесконечно. Для того чтобы преодолеть этот недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности – вероятности попадания точки в область.
Классическое определение вероятности предполагает, что число элементарных исходов конечно. На практике встречаются опыты, для которых множество таких исходов бесконечно. Для того чтобы преодолеть этот недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности – вероятности попадания точки в область. .
. .
. . Диагональ квадрата равна
. Диагональ квадрата равна 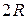 , тогда сторона квадрата равна
, тогда сторона квадрата равна  , а площадь квадрата равна
, а площадь квадрата равна  . Вероятность искомого события определяется как отношение площади квадрата к площади круга, т.е.
. Вероятность искомого события определяется как отношение площади квадрата к площади круга, т.е.  .
. не могут произойти все вместе в результате испытания, то будут ли они попарно несовместными?
не могут произойти все вместе в результате испытания, то будут ли они попарно несовместными? полную группу?
полную группу?


