
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типы распределений дискретных случайных величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть Х – дискретная случайная величина. Название закона распределения определяется тем, как находится вероятность возможных значений этой с.в.
Биномиальное распределение
Случайная величина Х имеет биномиальное распределение с параметрами n и р, если она принимает значения 0, 1, 2, …, n с вероятностями
Ряд распределения случайной величины, распределенной по биномиальному закону, имеет вид:
Биномиальное распределение является распределением числа «успехов» в n испытаниях Бернулли с вероятностью р «успеха» и вероятностью q = 1 – p «неудачи». Если Х подчиняется биномиальному распределению, то верны следующие соотношения: М(х)=np, D(x)=npq.
Гипергеометрическое распределение Случайная величина Х имеет гипергеометрическое распределение с параметрами N, M, n (N, M, n – натуральные числа,
где Ряд распределения случайной величины, распределенной по гипергеометрическому закону, имеет вид:
Гипергеометрическое распределение является распределением числа объектов, обладающих заданным свойством среди n объектов, случайно извлеченных без возвращения из совокупности объектов, из которых M обладают этим свойством.
Геометрическое распределение
Случайная величина Х имеет геометрическое распределение с параметрами р (0<p<1), если она принимает значения 1, 2, …, n, … с вероятностями
Геометрический закон распределения является распределением числа испытаний Бернулли до появления первого «успеха», включая последнее успешное испытание, если вероятность «успеха» в каждом испытании равна р. Действительно, чтобы осуществить событие Если Х подчиняется геометрическому распределению, то верны следующие соотношения:
Распределение Пуассона
Рассмотрим дискретную с.в. Х, которая может принимать только целые неотрицательные значения, образующие бесконечную последовательность: 0, 1, 2, …, m, … Говорят, что случайная величина Х распределена по закону Пуассона, если вероятность того, что она примет определенное значение m, выражается формулой
где Ряд распределения случайной величины, распределенной по закону Пуассона, имеет вид
Если Х подчиняется распределению Пуассона, то верны следующие соотношения: М(х)=λ, D(x)=λ. Характерной особенностью распределения Пуассона является равенство математического ожидания и дисперсии параметру Контрольные вопросы
15. Какое распределение вероятностей называется биномиальным распределением? 16. Какой смысл имеет с.в., распределенная по биномиальному закону с параметрами n и р? 17. Какое распределение вероятностей называется гипергеометрическим распределением? 18. Какими параметрами характеризуется гипергеометрическое распределение? 19. Какой смысл имеет с.в., распределенная по гипергеометрическому закону? 20. Какое распределение вероятностей называется геометрическим распределением? Чем объясняется такое название распределения? 21. Какой смысл имеет с.в., распределенная по геометрическому закону с параметром р? 22. Какое распределение вероятностей называется распределением Пуассона? 23. Почему закон распределения Пуассона также называют законом «редких событий»? 24. Как выглядят формулы для математического ожидания и дисперсии биномиального распределения? 25. Как выглядят формулы для математического ожидания и дисперсии геометрического распределения? 26. Как выглядят формулы для математического ожидания и дисперсии распределения Пуассона? Контрольные задания
1. Доказать, что последовательность вероятностей, задаваемая формулой
2. Доказать, что математическое ожидание случайной величины, распределенной по геометрическому закону удовлетворяет формуле 3. Доказать, что дисперсия случайной величины, распределенной по геометрическому закону удовлетворяет формуле 4. Доказать, что последовательность вероятностей, задаваемая формулой Пуассона, может представлять собой ряд распределения, т.е. сумма вероятностей 5. Доказать, что математическое ожидание случайной величины, распределенной по закону Пуассона удовлетворяет формуле М(Х)= = 6. Доказать, что дисперсия случайной величины, распределенной по закону Пуассона удовлетворяет формуле D(Х)= 7. Доказать, что сумма двух независимых случайных величин, распределенных по закону Пуассона с параметрами а и b является также случайной величины, распределенной по закону Пуассона с параметром а + b.
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 805; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.55.1 (0.01 с.) |

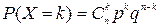 , k = 1, 2, …, n, q = 1 – p.
, k = 1, 2, …, n, q = 1 – p.
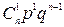

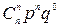
 ,
,  ), если она принимает значения
), если она принимает значения  с вероятностями
с вероятностями ,
,  ,
, ,
,  .
.
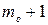

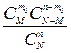
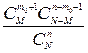

 ,
,  , k = 1, 2, …, n, …
, k = 1, 2, …, n, … необходимо, чтобы произошло подряд
необходимо, чтобы произошло подряд  «неудач» с вероятностью
«неудач» с вероятностью 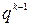 , а затем «успех» с вероятностью р.
, а затем «успех» с вероятностью р. ;
; 
 ,
, , m =0, 1, …
, m =0, 1, …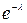



 .
.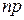 .
.


