
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятность попадания нормально распределенной случайной величины в заданный интервал. Правило трёх сигмаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Найдем функцию распределения случайной величины Х, подчиненной нормальному закону распределения:
сделаем в интеграле замену
Интеграл
Вероятность попадания случайной величины Х на участок (α, β) выражается формулой:
С помощью последней формулы можно оценить вероятность отклонения нормальной случайной величины от своего математического ожидания на заранее заданную сколь угодно малую положительную величину ε:
То есть
Пусть В этом состоит правило трех сигм: если случайная величина распределена нормально, то абсолютная величина отклонения ее значений от математического ожидания не превосходит утроенного среднего квадратического отклонения. Задача. Пусть диаметр изготовляемой цехом детали является случайной величиной, распределенной нормально, m = 4,5 см, Решение. Данная задача характеризуется следующими значениями параметров, определяющих искомую вероятность:
Контрольные вопросы
1. Какое распределение вероятностей называется равномерным? 2. Какой вид имеет функция распределения случайной величины, равномерно распределенной на отрезке [ а; b ]? 3. Как вычислить вероятность попадания значений равномерно распределенной случайной величины в заданный промежуток? 4. Как определяется показательное распределение случайной величины? 5. Какой вид имеет функция распределения случайной величины, распределенной по показательному закону? 6. Какое распределение вероятностей называется нормальным? 7. Какими свойствами обладает плотность нормального распределения? Как влияют параметры нормального распределения на вид графика плотности нормального распределения?
8. Как вычислить вероятность попадания значений нормально распределенной случайной величины в заданный промежуток? 9. Как вычислить вероятность отклонения значений нормально распределенной случайной величины от ее математического ожидания? 10. Сформулируйте правило «трех сигма»? 11. Чему равны математическое ожидание, дисперсия и среднее квадратическое отклонение случайной величины, распределенной по равномерному закону на отрезке [ а; b ]? 12. Чему равны математическое ожидание, дисперсия и среднее квадратическое отклонение случайной величины, распределенной по показательному закону с параметром λ? 13. Чему равны математическое ожидание, дисперсия и среднее квадратическое отклонение случайной величины, распределенной по нормальному закону с параметрами m и Контрольные задания
1. Случайная величина Х распределена равномерно на отрезке [−3, 5]. Найти плотность распределения и функцию распределения Х. Построить графики обеих функций. Найти вероятности 2. Автобусы маршрута №21 идут регулярно с интервалом 10 мин. Пассажир выходит на остановку в случайный момент времени. Рассматривается случайная величина Х − время ожидания пассажиром автобуса (в мин.). Найти плотность распределения и функцию распределения Х. Построить графики обеих функций. Найти вероятность того, что пассажиру придется ждать автобуса не более пяти минут. Найти среднее время ожидания автобуса и дисперсию времени ожидания автобуса. 3. Установлено, что время ремонта видеомагнитофона (в днях) есть случайная величина Х, распределенная по показательному закону. Среднее значение времени ремонта видеомагнитофона равно 10 дням. Найти плотность распределения и функцию распределения Х. Построить графики обеих функций. Найти вероятность того, что на ремонт видеомагнитофона потребуется не менее 11 дней. 4. Изобразите графики плотности и функции распределения случайной величины Х, распределенной по нормальному закону с параметрами m = = − 2 и 5. Найти М (1− Х) и D (1− Х) случайной величины Х, плотность распределения которой 6. Случайная величина Х распределена нормально, причем m = 10 и
7. Автомат изготавливает подшипники, которые годными, если отклонение Х от проектного размера по модулю не превышает 0,77 мм. Каково наиболее вероятное число годных подшипников из 100, если случайная величина Х распределена нормально с параметром
Литература 1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2002. – Гл. 6 – 8, гл. 10, гл. 11, гл. 12, п.п. 1 – 7, гл. 13. 2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2002. – Гл. 4, гл.6. 3. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1999. – Гл. 5, гл. 6.
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1753; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.63.107 (0.01 с.) |

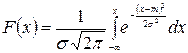 ,
,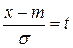 и приведем его к виду:
и приведем его к виду: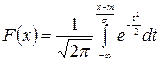 .
.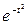 или
или  . Выразим функцию
. Выразим функцию 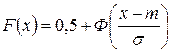 .
.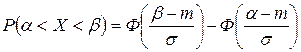 .
.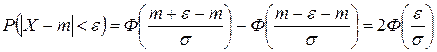 ,
,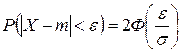 .
.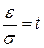 , тогда
, тогда 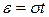 и
и 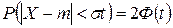 . При t =3 получим
. При t =3 получим  , т.е. событие, заключающееся в том, что отклонение нормально распределенной случайной величины от математического ожидания, будет меньше
, т.е. событие, заключающееся в том, что отклонение нормально распределенной случайной величины от математического ожидания, будет меньше 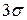 , является практически достоверным.
, является практически достоверным.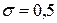 см. Найти вероятность того, что размер диаметра наудачу взятой детали отличается от ее математического ожидания не более, чем на 1 мм.
см. Найти вероятность того, что размер диаметра наудачу взятой детали отличается от ее математического ожидания не более, чем на 1 мм.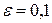 ,
, 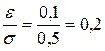 , Ф(0,2)=0,0793,
, Ф(0,2)=0,0793, 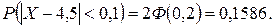
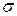 ?
?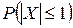 и
и 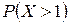 . Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение Х.
. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение Х.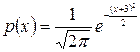 .
.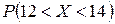 .
.


