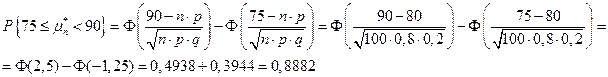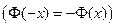Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 2. Случайные величины.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
§1. Определение случайной величины.
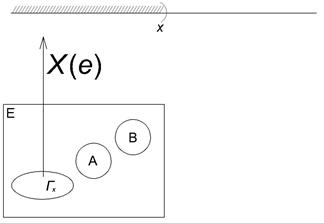
Пусть (Е, К, Р) – вероятностная модель некоторого случайного опыта. Рассмотрим примеры числовых функций, аргументом которых является элементарное событие. Пример. 1. Опыт: бросается монета
2. Рассмотрим схему Бернулли с числом испытаний n и вероятностью успеха p.
Каждому элементарному событию e из Е поставим в соответствие число, равное количеству символов У, сколько есть в такой последовательности. Тем самым мы определили числовую функцию 3. На отрезок АВ числовой оси случайным образом бросается точка.
Рассмотрим событие
Случайная величина. Случайная величина и числовая функция элементарного события – это не одно и то же. Мало задать числовую функцию, надо знать вероятности множества значений, которые может принимать эта функция. Определение. Случайной величиной называется числовая функция элементарного события е, определённая на пространстве элементарных событий Е такая, что для любого
Рассмотрим
§2. Функция распределения случайной величины и её свойства.
Определение. Функцию
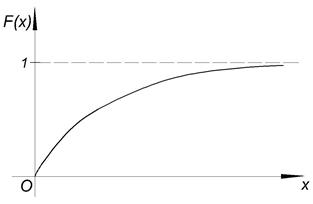
Эту функцию называют функцией распределения случайной величины Х. Свойства функции распределения случайной величины: 1. 2. Доказательство.
3. F (x) – неубывающая функция,
По свойству 2 4. Если функция F (x) непрерывна при x = x1, то P { X = x1 }=0. Функция y = f (x) непрерывна при x = x1, если Дадим Δx, подсчитаем ΔF: При 5. Укажем без доказательства следующее свойство: 6. 7. F (x) – непрерывна слева:
§3. Дискретные случайные величины.
Случайные величины различны по природе. Нужные в практике удовлетворяют случайные величины дискретные и непрерывные. Случайная величина называется дискретной, если множество её возможных значений является конечным или счётным.
Дискретная случайная величина полностью определена, если заданы вероятности этих возможных значений.
Обычно дискретную случайную величину (закон распределения случайной величины) задают таблицей.
Таблица 1
Эту таблицу называют рядом распределения случайной величины. Пример. Бросаются две игральные кости: зелёная и красная. Рассматривается случайная величина х – сумма выпавших очков на двух костях. Составить закон распределения этой случайной величины.
X = i + j
Закон распределения может быть задан функцией распределения дискретной случайной величины. Дискретная случайная величина задана:
Найти функцию распределения и построить её график.
График распределения имеет ступенчатый вид. Скачки происходят в точках, соответствующих возможным значениям и скачки равны вероятности этих значений.
Примеры дискретных распределений случайной величины: 1. В схеме Бернулли с n испытаниями рассмотрим случайную величину X (e)= m – суммарное число успехов за n испытаний. 0, 1, 2, …, n – возможные значения случайной величины.
Распределение X (e) суммарного числа успехов в схеме Бернулли называется биномиальным распределением. Биномиальный ряд распределения случайной величины:
Пример. Устройство состоит из трёх независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте – 0,1. Составить закон распределения числа отказавших элементов в одном опыте. Случайная величина Х – число отказавших элементов в одном опыте. У – отказ; Р (У)=0,1; q =0,9
Закон Пуассона. Закон приближения биномиального распределения в случае, когда р – весьма мала, n – весьма велико.
Пусть
(1) Распределение дискретной случайной величины согласно (1) называется распределением Пуассона. Это распределение зависит только от а. Пример. Завод отправил на базу 5000 изделий. Вероятность того, что в пути изделие повредится – 0,0002. найти вероятность того, что на базу прибудут 3 негодных изделия. p =0,0002; k =3; n =5000
§4. Непрерывные случайные величины.
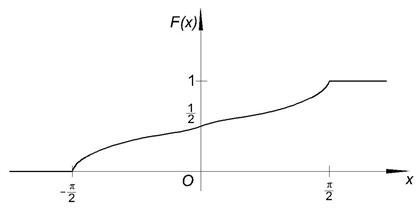
Под непрерывной случайной величиной понимают случайную величину, возможные значения которой сплошь заполняют некоторый промежуток. Определение 1. Пусть F (x) – функция распределения случайной величины Х, F (x) – дифференцируема: Случайная величина Определение 2. Функция
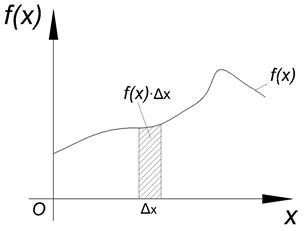
В числителе вероятность того, что случайная величина принимает значение в интервале длиной Δх. Отношение под знаком lim задаёт вероятность, приходящуюся на единицу длины. Беря предел, получим плотность вероятностей. График функции f (x) называется кривой распределения. Заметим, что f (x) существует только для непрерывной случайной величины. Из (*) Отбрасывая бесконечно малую более высокого порядка, получаем приближённое значение.
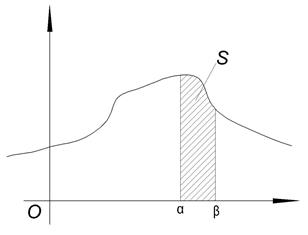
Из (1) Теорема. Вероятность того, что непрерывная случайная величина принимает значение в интервале от α до β Доказательство.
F (x) – первообразная для f (x)
По формуле Ньютона-Лейбница
Геометрически:
Свойства f ( x ): 1°. Доказательство: 2°.
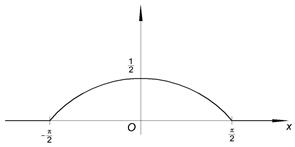
Геометрически 1° и 2° означают, что график функции f (x) расположен выше либо на оси ОХ и площадь под кривой f (x)=1. Пример. Задана функция 1) определить а; 2) построить график f (x); 3) определить F (x) и график; 4) 1) Найдём а:
2)
4)
§5. Числовые характеристики случайных величин.
Наиболее полной характеристикой случайной величины является закон её распределения, он даёт все сведения о случайной величине: какие возможные значения она может принимать и с какими вероятностями. Закон распределения случайной величины задаётся функцией распределения F (x) или функцией плотности распределения f (x). На практике часто закон распределения неизвестен, а с другой стороны, нас интересуют более частные сведения, поэтому пользуются более общими характеристиками случайных величин, которые выражают наиболее существенные особенности распределения. Их называют числовыми характеристиками случайной величины: 1) среднее значение или математическое ожидание случайной величины 2) дисперсия случайной величины 3) моменты случайных величин Каждая из этих характеристик с определённой стороны характеризует случайную величину. Математическое ожидание. 1) Дискретная случайная величина. Пусть дан ряд распределения дискретной случайной величины
Математическим ожиданием дискретной случайной величины называется сумма попарных произведений возможных значений случайной величины на их вероятности.
Выясним вероятностный смысл математического ожидания. Пусть произведено n опытов, в результате которых случайная величина X приняла значения: x1 – m1 раз x2 – m2 раз … xk – mk раз m1 + m2 +…+ mk = n Подсчитаем сумму всех значений, которые случайная величина приняла в n опытах. x1m1 + x2m2 +…+ xkmk – сумма всех значений случайной величины за n опытов. Вычислим среднее значение, которое принимает одна величина.
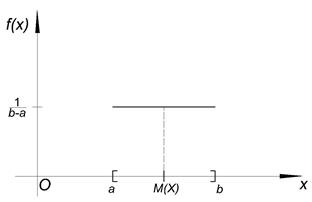
При большом n частоты будут приближаться к соответствующим вероятностям При большом числе опытов среднее значение величины равно значению её математического ожидания. На числовой оси возможные значения случайной величины располагают слева и справа от математического ожидания. Таким образом, математическое ожидание характеризует расположение распределения на числовой оси. 2) Непрерывная случайная величина. Рассмотрим непрерывную случайную величину, у которой известна плотность распределения f (x), и которая принимает возможные значения на [ a, b ].
Рассмотрим разбиение [ a, b ] точками деления x0, x1, x2, …, xk, xk+1, …, xn = b Δxk – длина k -го отрезка разбиения
Если λ достаточно мало, то приближённо можно считать, что Таким образом, мы фактически можем перейти от непрерывной случайной величины к дискретной случайной величине, которая может принимать возможные значения
Чем меньше λ, тем точнее математическое ожидание характеризует значение непрерывной случайной величины. Чтобы получить точное равенство, перейдём к причём в правой части равенства предела Так как по определению функция f (x) интегрируема всюду, то предел интегральной суммы существует и равен
Если случайная величина принимает значения на всей числовой оси, то математическое ожидание нужно считать на всей числовой оси.
Определение. Математическим ожиданием непрерывной случайной величины называется интеграл Свойства математического ожидания: 1°. 2°. 3°. 4°.
Дисперсия.
Дисперсия – какой разброс имеют возможные значения случайной величины от математического ожидания. Введём случайную величину
Затем решили перейти к Определение. Дисперсией случайной величины называется математическое ожидание квадрата соответствующей центрированной случайной величины.
Формулы для вычисления дисперсии: 1) дискретная случайная величина 2) непрерывная случайная величина Дисперсия имеет размерность квадрата случайной величины. Для наглядной оценки рассеивания удобно пользоваться характеристикой, размерность которой совпадает с размерностью случайной величины.
Математическое ожидание и дисперсия характеризуют наиболее важные черты распределения случайной величины – его расположение и степень разбросанности. Свойства дисперсии: 1°. 2°. 3°. Если X, Y – независимые случайные величины, то Примеры непрерывных случайных величин. 1. Равномерно распределённая на [ a, b ] случайная величина Х. Опыт: на отрезок [ a, b ] бросается точка
2. Показательное распределение.
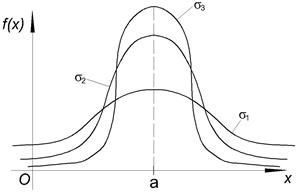
§6. Нормальный закон распределения случайной величины.
Это наиболее часто встречающийся на практике закон распределения.
Убедимся в том, что а – математическое ожидание, а σ – среднее квадратическое отклонение нормального распределения ( 1) Будем вычислять интеграл методом замены переменной
Замена
§7. Функция плотности, кривая Гаусса.
§8. Вероятность попадания на заданный интервал нормальной случайной величины.
Замена
Пример. Случайная величина подчинена нормальному закону
a =30; σ =10, найти
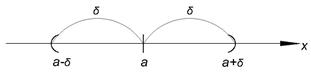
§9. Вероятность заданного отклонения.
Пусть δ >0 – заданное положительное число. Найти
§10. Правило трёх сигм.
Положим δ=3σ, найдём
Если случайная величина распределена нормально, то абсолютная величина её отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения. На практике правило используют так: если распределение неизвестно, но выполняется это правило, то есть основания предполагать, что случайная величина распределена нормально.
Предельные теоремы теории вероятностей устанавливают закономерности при массовом проявлении случайных явлений. Нельзя предсказать исход отдельного случайного явления, но оказывается, что средний результат массы случайных явлений является закономерным и может быть предсказан с большой степенью определённости.
§11. Закон больших чисел.
Закон больших чисел – это совокупность теорем, которые устанавливают с вероятностью как угодно близкой к единице, что наступит некоторое событие, зависящее от неограниченного увеличивающегося числа случайных факторов. Влияние каждого фактора мало по сравнению с суммарным действием всех факторов. Пусть дана последовательность случайных величин:
Говорят, что последовательность (1) удовлетворяет закону больших чисел, если т.е. с вероятностью, как угодно близкой к единице наступит событие, состоящее в том, что уклонение среднего арифметического достаточно большого числа случайных величин от среднего арифметического их математических ожиданий будет сколь угодно малым по абсолютной величине.
§12. Неравенство Чебышёва.
Даёт оценку вероятности больших уклонений случайной величины от математического ожидания. Х - случайная величина, D (X) – дисперсия, Доказательство. (проведём для непрерывной случайной величины)
§13. Теорема Чебышёва.
x1, x2, …, xn, … (1) 1. Случайные величины Xk – попарно независимы. 2. Дисперсии этих случайных величин равномерно ограничены: Тогда (1) удовлетворяет закону больших чисел. Доказательство. Рассмотрим случайную величину
Тогда запишем для этой случайной величины неравенство Чебышёва
§14. Теорема Бернулли.
Это частный случай теоремы Чебышёва. Производится n независимых опытов, каждый опыт имеет 2 исхода: успех – p, неудача – q.
Утверждение теоремы: Доказательство. Теорема сразу следует из теоремы Чебышёва, если заметить, что случайную величину
Докажем, что в этом случае выполняются условия теоремы Чебышёва: 1) xk – попарно независимы 2) дисперсии равномерно ограничены
Последовательность случайных величин x1 + x2 +…+ xn удовлетворяет всем условиям теоремы Чебышёва, поэтому она удовлетворяет закону больших чисел (*).
§15. Центральная предельная теорема.
Общий смысл центральной предельной теоремы заключается в следующем: если случайная величина представляет собой сумму слабо зависимых слагаемых и каждое слагаемое невелико по сравнению со всей суммой, то независимо от природы этих слагаемых, т.е. от того, какой они имеют закон распределения, с ростом числа слагаемых распределение этой случайной величины сближается с нормальным законом.
§16. Теорема Муавра-Лапласа.
Пусть производится n независимых опытов, каждый опыт имеет 2 исхода:
Рассмотрим случайную величину Утверждение теоремы:
(1) Вероятность попадания случайной величины Без доказательства. Нормальная сумма:
поэтому равенство (1) можно записать более подробно
Пример. Произведено 100 независимых испытаний (n =100), p =0,8. Найти вероятность того, что случайная величина
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 493; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.104.36 (0.009 с.) |

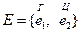

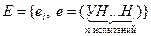
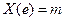 , m – суммарное число успехов за n испытаний, возможных значений
, m – суммарное число успехов за n испытаний, возможных значений  .
.

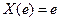 . Возможные значения этой функции сплошь занимают отрезок АВ.
. Возможные значения этой функции сплошь занимают отрезок АВ.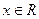 определены вероятности событий
определены вероятности событий 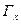 , где
, где  .
. . Числовая функция
. Числовая функция 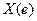 осуществляет отображение пространства Е на числовую ось.
осуществляет отображение пространства Е на числовую ось.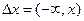
 Требуется, чтобы
Требуется, чтобы  . В противном случае это не будет событием.
. В противном случае это не будет событием.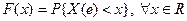 называют функцией распределения.
называют функцией распределения.
 в соответствии с аксиомой 1 и 2.
в соответствии с аксиомой 1 и 2.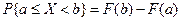
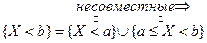

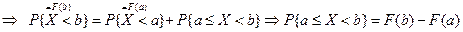 .
.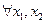 -
- 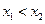

 .
. .
.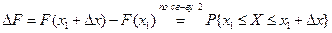
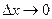 получим
получим 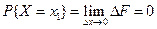 , т.к. F (x) непрерывна при x = x1.
, т.к. F (x) непрерывна при x = x1.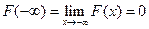 .
.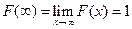 .
.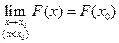 .
.
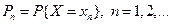 , Pn ≥0
, Pn ≥0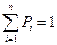

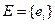 ,
, 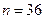 ,
, 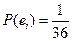
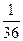
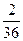
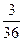


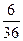




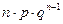
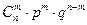

 ;
;  ;
; 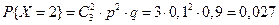 ;
; 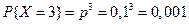 .
.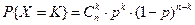 (*)
(*)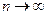 ,
, 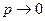 , но
, но 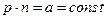 .
.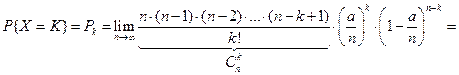
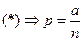


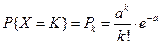 ,
,  .
.
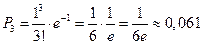 .
. .
. неотрицательная функция f (x), интегрируемая на всей числовой оси и такая, что
неотрицательная функция f (x), интегрируемая на всей числовой оси и такая, что 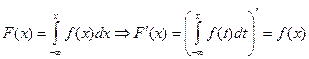 .
.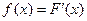 называется плотностью распределения и плотностью вероятностей непрерывной случайной величины.
называется плотностью распределения и плотностью вероятностей непрерывной случайной величины.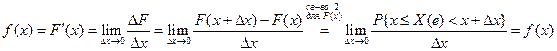 (*)
(*)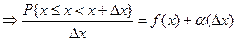 ;
; 
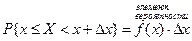
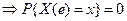 .
.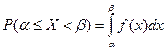 .
.
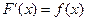
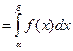 .
.

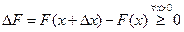 , т.к. по свойству 3 F (x) – неубывающая. Тогда
, т.к. по свойству 3 F (x) – неубывающая. Тогда  .
.

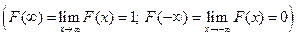
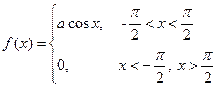
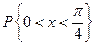 .
.

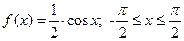
 3)
3) 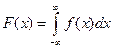
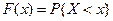
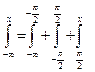

 .
.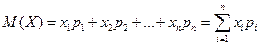
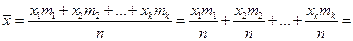
 - частота события
- частота события 

 (
(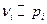 )
)
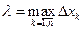 - параметр разбиения
- параметр разбиения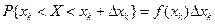
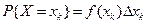 .
.

 стоит интегральная сумма для
стоит интегральная сумма для 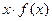 на [ a, b ].
на [ a, b ].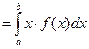 .
.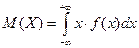
 , при этом предполагается, что несобственный интеграл сходится абсолютно, т.е. существует
, при этом предполагается, что несобственный интеграл сходится абсолютно, т.е. существует  .
.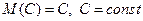 .
.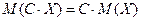 .
.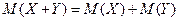 .
.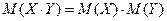 , если X и Y – независимые случайные величины.
, если X и Y – независимые случайные величины.
 - центрированная случайная величина.
- центрированная случайная величина. нельзя взять за характеристику рассеяния возможных значений, т.к.
нельзя взять за характеристику рассеяния возможных значений, т.к. 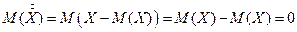 .
.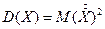 - дисперсия.
- дисперсия.
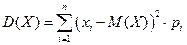
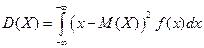
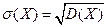 - среднее квадратическое отклонение случайной величины.
- среднее квадратическое отклонение случайной величины.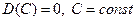 .
. .
.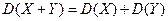 .
.
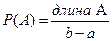
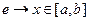
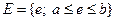
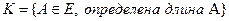
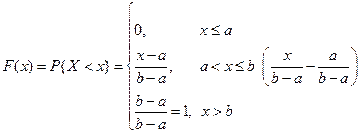

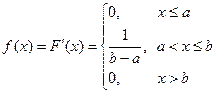

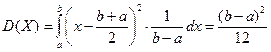
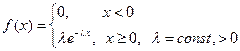


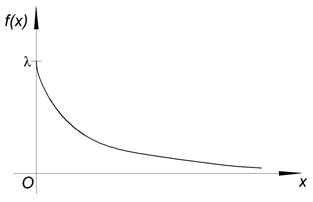
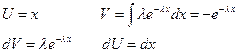
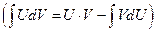

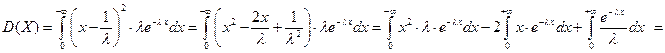
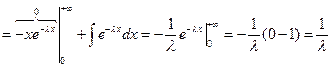
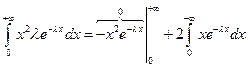





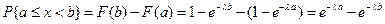

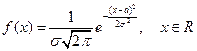 - это распределение также называется законом Гаусса.
- это распределение также называется законом Гаусса. ).
).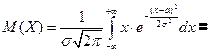
 пределы интегрирования не меняются, т.к. замена линейная.
пределы интегрирования не меняются, т.к. замена линейная.

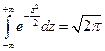 - неберущийся интеграл, интеграл Эйлера-Пуассона
- неберущийся интеграл, интеграл Эйлера-Пуассона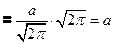
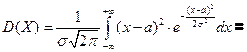
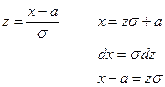
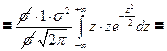
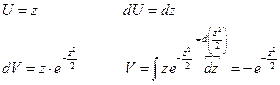

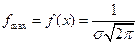
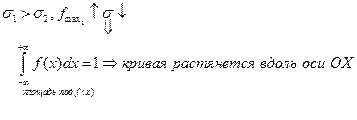 Если σ =1, a =0, то
Если σ =1, a =0, то 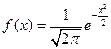 случайная величина имеет стандартное нормальное распределение.
случайная величина имеет стандартное нормальное распределение.



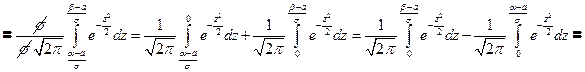
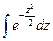 - неберущийся, т.е. не выражается через элементарные функции, пользуются табл. спец. функции, функцией Лапласа или интегралом вероятности:
- неберущийся, т.е. не выражается через элементарные функции, пользуются табл. спец. функции, функцией Лапласа или интегралом вероятности: 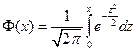 .
. .
.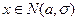
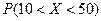 .
.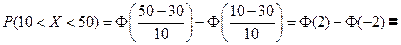
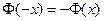
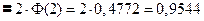 .
.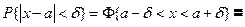
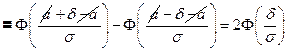


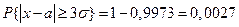
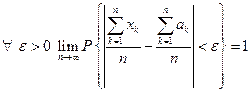 ,
,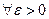 , тогда
, тогда 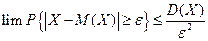 .
.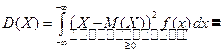


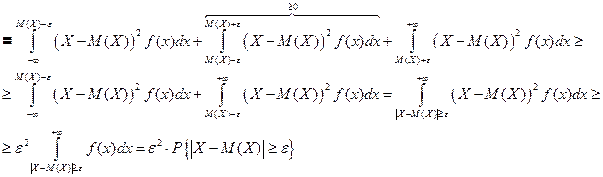
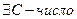 :
: 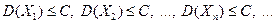
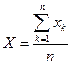
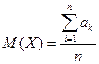

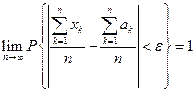 .
.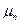 - суммарное число успехов за n испытаний.
- суммарное число успехов за n испытаний.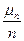 - частота успеха.
- частота успеха.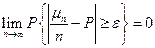 (*)
(*)
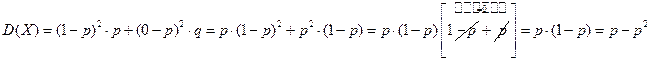
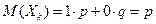



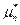 на (a, b) считается для нормальной случайной величины.
на (a, b) считается для нормальной случайной величины.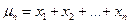
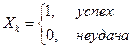
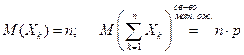
 ,
, .
.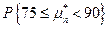 .
.