Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывные случайные величиныСодержание книги Поиск на нашем сайте
Непрерывную случайную величину невозможно задать, указывая вероятности, с которыми принимаются ее значения. Вероятность принять фиксированное значение равна 0. Имеет смысл говорить только о вероятности попадания в заданный промежуток. На этом основан способ задания случайной величины с помощью функции распределения, которая может быть определена для всех типов случайных величин, а не только для непрерывных. Определение. Функцией распределения случайной величины Х называется функция F (x) = P (X < x). Пример 1. Построить функцию распределения случайной величины Х:
Изобразить ее график. Решение. Если x £ 0, то событие X < x невозможное: у Х нет значений, меньших 0. Поэтому для этого случая F (x) = 0. Если 0 < x £ 1, то событие X < x означает, что Х = 1: это единственное значение Х, меньшее таких х. Поэтому для этого случая F (x) = 0,3. Если 1 < x £ 3, то событие X < x означает, что Х принимает значение 0 или 1. Суммируя соответствующие вероятности, получаем для этого случая F (x) = 0,3 + 0,6 = 0,9. Наконец, если x > 3, то событие X < x достоверное: все значения Х удовлетворяют неравенству X < x для таких х. Поэтому для этого случая F (x) = 1. Следовательно, функция распределения имеет вид
Ее график:
Замечание. Соблюдать на графике одинаковый масштаб по осям абсцисс и ординат нет необходимости, так как по этим осям откладываются разнородные величины. В приведенном примере график функции распределения разрывный, так как случайная величина дискретная. Для непрерывной случайной величины график функции распределения непрерывный. Теорема 1.10.1. Свойства функции распределения. 1*. 0 £ F (x) £ 1. 2*. F (– ¥) = 0, F (+¥) = 1 (имеются в виду соответствующие пределы). 3*. Р (a < Х < b) = F (b) – F (a) (строгие неравенства можно заменить нестрогими). Дадим графическую иллюстрацию последней формулы.
На рисунке вероятности попадания в промежутки (a, b) и (c, d) равны длинам соответствующих отрезков, выделенных на оси ординат жирными линиями. Видим, что хотя интервал (a, b) значительно короче (c, d), вероятность попадания в него больше. Причина этого в том, что на первом интервале график F (x) значительно круче, то есть функция F (x) возрастает быстрее. Но крутизна графика функции характеризуется ее производной, график которой дает более наглядное представление о скорости возрастания функции, чем график самой функции. На этом основан другой способ задания непрерывной случайной величины. Определение. Плотностью вероятности случайной величины Х называется производная от ее функции распределения, то есть f (x) = F ¢(x). Теорема 1.10.2. Свойства плотности вероятности. 1*. f (x) ³ 0. 2*. 3*. Р (a < Х < b) = 4*. F (x) = Геометрический смысл свойства 2*: площадь под графиком функции f (x) равна 1. Геометрический смысл свойства 3*: вероятность попадания случайной величины в интервал (a, b) равна площади криволинейной трапеции, ограниченной осью абсцисс, графиком f (x) и прямыми x = a, x = b. С помощью плотности вероятности можно вычислить числовые характеристики непрерывной случайной величины. Математическое ожидание: МХ = Дисперсия: DX = M (X 2) – M (X)2, где M (X 2) = Пример 2. Дана функция распределения случайной величины Х:
Найти ее плотность вероятности. Построить графики функции распределения и плотности вероятностей. Найти MX, DX, σ(X) и вероятность того, что 1< Х < 3.
Графики функций приведены на рисунках. Замечание. График функции распределения должен быть непрерывным. График плотности вероятностей может иметь разрывы, что мы и видим на рисунке. Это отразилось и на области определения этой функции: в точке 0 она определена, в точке 2 не определена. МХ = M (X 2) = DX = M (X 2) – M (X)2 = 2 – σ(X) = Р (1< Х < 3) = F (3) – F (1) = 1 – Упражнения 10.1. Дана функция распределения случайной величины Х:
Найдите ее плотность вероятности. Постройте графики функций F (x)и f (x). Найдите MX, DX, σ(X) и вероятность того, что –1< Х < 1. 10.2. Значения случайной величины Х принадлежат отрезку [1; 5]. Плотность вероятности на этом отрезке постоянна, f (x) = p. Найдите значение р. 10.3. Значения случайной величины Х принадлежат отрезку [0; 4]. Плотность вероятности на этом отрезке имеет вид f (x) = cx. Найдите значение c.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 221; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.247.170 (0.005 с.) |




 = 1.
= 1. (строгие неравенства можно заменить нестрогими).
(строгие неравенства можно заменить нестрогими). .
.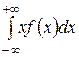 .
. .
.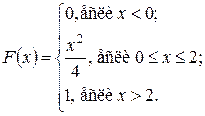
 Решение.
Решение.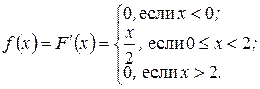
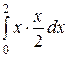 =
= 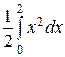 =
= 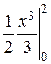 =
= 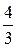 ;
;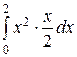 =
= 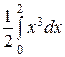 =
=  = 2;
= 2;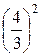 =
=  ;
;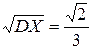 ;
;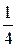 = 0,75.
= 0,75.