
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные законы распределения случайных величин.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Основными законами распределения для дискретных случайных величин являются следующие. Равновозможное распределение. Случайная величина принимает n значений с одинаковой вероятностью, равной 1/ n. Такое распределение имеет место в схеме с классическим определением вероятности. Биномиальное распределение. Это распределение для числа успехов в схеме Бернулли с п испытаниями и вероятностью успеха в одном испытании р. Число успехов принимает значения от 0 до п, вероятность для каждого значения определяется формулой Бернулли Рn (m) = Для непрерывных случайных величин имеем следующие основные законы распределения. Равномерное распределение. Случайная величина принимает значения на отрезке [ a, b ] с постоянной плотностью вероятности. Значение плотности вероятности Нормальное распределение. Это наиболее часто встречающееся на практике распределение. Плотность вероятности задается формулой
График плотности вероятности имеет вид холма. Абсцисса вершины холма находится в точке а, это математическое ожидание случайной величины.
Точки перегиба графика имеют абсциссы, отстоящие от а на σ в обе стороны. Среднее квадратичное отклонение равно σ. Площадь фигуры, ограниченной графиком и осью абсцисс, равна 1. Примерно 2/3 этой площади сосредоточена на отрезке [ a – σ, a + σ], такова вероятность попадания значения случайной величины в этот отрезок. Действует правило трех сигм»: вероятность того, что значение случайной величины окажется вне отрезка [ a – 3σ, a + 3σ], равна 0,3%, то есть это практически невозможное событие. Нормальное распределение полностью задается своими параметрами а и σ. При изменении а холм передвигается вправо или влево. При изменении σ меняется крутизна холма при этом площадь под ним остается равной 1. При увеличении σ холм становится более пологий, при уменьшении – более крутой. В соответствии с правилом трех сигм это означает, что при уменьшении σ разброс значений случайной величины становится все меньше, то есть эта величина становится все более определенной.
Закон больших чисел Закон больших чисел– это серия теорем, описывающих поведение случайной величины, являющейся суммой большого числа других случайных величин. Центральная предельная теорема. Если случайная величина является суммой большого числа других случайных величин, дисперсии которых не слишком отличаются друг от друга, то закон распределения суммы близок к нормальному. Здесь приведена не точная формулировка, а смысл центральной предельной теоремы. Условие на дисперсии достаточно относительно, оно означает, что каждая случайная величина в отдельности влияет на сумму незначительно. Проявляется эта теорема, например, в схеме Бернулли. При проведении п независимых испытаний каждому испытанию можно сопоставить случайную величину – число успехов в этом испытании. Эта случайная величина может принимать одно из значений 0 или 1 с вероятностями р и q соответственно; закон ее распределения весьма далек от нормального. Число успехов в п испытаниях есть сумма этих случайных величин. Если отметить на графике вероятности ее значений, например, для п = 10, то точки образуют фигуру, похожую на холм. При больших же значениях п действуют теоремы Муавра – Лапласа, основанные на нормальном законе распределения. Простейшей формой закона больших чисел является теорема Бернулли, на которой основано статистическое определение вероятности: увеличением числа испытаний п в схеме Бернулли отклонение относительной частоты появления успеха m/n от его вероятности р можно сделать как угодно малым. Какое бы малое значение отклонения ε ни задать, Обобщением этой теоремы является теорема Чебышёва, или закон больших чисел в форме Чебышёва. Смысл ее следующий. Пусть имеется большое число независимых случайных величин с ограниченной дисперсией (то есть каждая в отдельности ничтожно мало влияет на их сумму). Тогда среднее арифметическое этих случайных величин (само являющееся случайной величиной) имеет малый разброс относительно своего математического ожидания. Практическое значение этой теоремы проявляется, например, при измерении физической величины. В результате измерений могут быть ошибки, но если произвести большое количество измерений и взять среднее арифметическое результатов, то получим очень хорошую точность. Эта точность может значительно превосходить возможности прибора, которым производятся измерения. Закон больших чисел проявляется в природе. В биологии он объясняет, например, почему примерно на одном уровне поддерживается численность организмов различных видов там, где нет активного вмешательства человека в природу. В физике на микроскопическом уровне мы можем наблюдать явление броуновского движения. На мельчайшую каплю масла, плавающую в жидкости, постоянно действуют силы ударов со стороны хаотически движущихся молекул жидкости. Равнодействующая этих сил является случайной величиной (векторной). Значение этой случайной равнодействующей постоянно меняется по величине и направлению, а среднее значение нулевое. Под воздействием равнодействующей силы капля совершает хаотические перемещения, подчиняясь физическому закону F = ma, связывающему силу, массу и ускорение. Если массу капли увеличить в 2 раза, то, чтобы сделать такой же скачок, она должна получить воздействие в 2 раза большей силы. Но вероятность этого значительно меньше, а при большом увеличении массы капли она становится практически равной нулю. Поэтому у больших, видимых глазом капель никакого движения не наблюдается. Вероятностную природу в основе имеют законы, описывающие поведение газов. Газ состоит из большого числа хаотически движущихся молекул. При небольшом их числе молекулы могли бы заполнять объем, в котором находятся, неравномерно, могли иногда скапливаться в одной половине занимаемого помещения. Но при таком количестве молекул, которое мы реально имеем, вероятность этого не просто ничтожно мала, она ничтожно мала даже для всего времени существования вселенной. Поэтому законы газовой динамики имеют не вероятностную, а строгую физическую форму.
Задания для контрольной работы Каждый студент подставляет в задания свои значения параметров а и b. 1. Сколькими способами из группы в (10+ a+b) человек можно выбрать двоих делегатов на конференцию? 2. Сколькими способами из группы в (15+ a+b) человек можно выбрать старосту и его заместителя? 3. По мишени производятся три выстрела. Выразить через события Аk – «попадание при k -ом выстреле», (k = 1, 2, 3), следующие события:
4. В урне 5 черных, а красных и b белых шара. Наудачу вынимаются 3 шара. Какова вероятность, что все они разного цвета? 5. Какова вероятность, что при бросании двух игральных кубиков в сумме выпадет a+b очков? 6. Два стрелка одновременно стреляют по мишени. Вероятности попадания для них равны соответственно 7. Из карточек с буквами составлена Ваша фамилия. Составьте из этих карточек (не обязательно всех) какое-нибудь слово. Какова вероятность, что при случайном извлечении нужного числа карточек и выкладывании их в ряд получится это слово? 8. На сборку поступают детали из двух цехов: 40% из первого и 60% из второго. В продукции первого цеха а % брака, второго – (a+b)%. Какова вероятность, что наудачу взятая деталь окажется бракованной? 9. Производятся 7 выстрелов по мишени с вероятностью попадания при одном выстреле а /10. Какова вероятность, что будет ровно b попаданий? Какое наиболее вероятное количество попаданий? 10.Производится 100 испытаний с вероятностью успеха в одном испытании 11.Случайная величина Х задана таблицей:
Найдите функцию распределения F (x) и постройте ее график. Найдите математическое ожидание, дисперсию и среднее квадратичное отклонение. 12.Непрерывная случайная величина задана Х функцией распределения:
Найдите плотность вероятности f (x). Найдите вероятность того, что Х примет значение из интервала
Математическая статистика. Выборочный метод Для того, чтобы принимать правильные решения в экономике, политике, коммерции и других областях деятельности, необходимо владеть информацией. Информацию получают как в процессе обычной работы из отчетов подразделений и других документов, так и в ходе специальных исследований, которые проводят статистические службы. Полученную информацию надо уметь обработать, чтобы на ее основе составлять прогнозы и планы. Прогнозы в экономике в условиях конкуренции должны быть очень точными. Если спрос на производимый товар окажется меньше ожидаемого, то это приведет к потерям на производство ненужного товара. Если же спрос окажется выше, то это будет означать недополученную прибыль. Совершенно точно спрогнозировать спрос, конечно невозможно, и надо уметь определять его границы и вероятность отклонения от этих границ. Принятое решение должно обеспечить максимальную прибыль. Объекты статистического изучения могут быть самые разные. Это может быть и распределение размеров одежды у потенциальных покупателей, и технические параметры произведенной промышленной продукции, и содержание полезных веществ в выращенной сельскохозяйственной продукции, и оценки учеников на экзаменах, и многое другое. Изучаемая в данном статистическом исследовании совокупность объектов называется генеральной совокупностью; количество этих объектов – объем генеральной совокупности. Выделяется один или несколько параметров, которые необходимо изучить. Значение параметра является случайной величиной, у каждого объекта генеральной совокупности оно свое. Задача статистики – определить закон распределения этой случайной величины. Если у каждого объекта генеральной совокупности можно измерить значение параметра, то мы получим полную и точную информацию о законе распределения. Но обычно это невозможно. Объем генеральной совокупности может быть очень большой. Изучение параметров продукции может сопровождаться ее уничтожением, например, при определении боевых характеристик произведенной партии снарядов. Поэтому для изучения генеральной совокупности из нее производят выборку, то есть отбирают некоторое количество объектов для непосредственного изучения. Обязательное условие для выборки – ее репрезентативность. Оно означает, что выборка должна равномерно представлять всю генеральную совокупность. Не является репрезентативной, например, выборка для изучения характеристик урожая яблок из сада, если в выборку попадают плоды с одного дерева. Не является репрезентативным и результат социологического опроса, производимого по телефону в рабочее время: участвовать в опросе будут в основном пенсионеры и домохозяйки. Выборка может быть повторной или бесповторной. При повторной выборке ее объекты отбираются по одному и после изучения возвращаются в генеральную совокупность. Каждый объект может попасть в выборку любое число раз. При бесповторной выборке все ее объекты различные. Оказывается, повторная выборка более правильно отражает распределение изучаемого признака в генеральной совокупности. Но если объем выборки мал по сравнению с объемом генеральной совокупности, то принципиальной разницы между повторной и бесповторной выборкой нет. Пусть изучается распределение значений признака Х (являющегося случайной величиной). В результате измерения получаем набор его значений для объектов выборки. Каждое его значение называется вариантой, а весь набор значений – вариационным рядом. Каждая варианта может встречаться один или несколько раз. Количество ее появлений ni в выборке называется ее частотой, а отношение ni / n частоты к общему объему выборки называется относительной частотой. Диаграмма, на которой показаны значения частот или относительных частот для вариант выборки, называется полигон частот. На этой диаграмме значения частот для каждой варианты отмечаются точками, и эти точки последовательно соединяются отрезками. Если значений вариант очень много, то их следует сгруппировать в интервалы, обычно одинаковой ширины. Количество и ширина интервалов определяются объемом выборки и задачами исследования. Например, при производстве одежды один из параметров – рост человека, для него приняты интервалы шириной 6 см. Частотой для каждого интервала будет количество значений изучаемого признака, попавших в этот интервал. Диаграмма, изображающая распределение частот для интервального распределения, называется гистограммой, она имеет столбчатую форму. Выделяются несколько числовых характеристик, описывающих вариационный ряд и позволяющих сравнивать вариационные ряды между собой. Выборочное среднее
Если для выборки объема п указаны выборочные значения x 1, …, xm и соответствующие частоты n 1, …, nm, то пользуемся формулой
Этой же формулой пользуемся, если вариационный ряд имеет интервальный вид. В качестве значений xi в этом случае берем середины соответствующих интервалов. Мода вариационного ряда – это варианта, встречающаяся чаще всех других. Если таких вариант несколько, то мода имеет несколько значений. Если все варианты встречаются одинаково часто (в частности, по одному разу), то моды нет. Смысл этого термина близок к смыслу обычного термина «мода»: это самое «модное» значение. Среди значений вариант может встретиться значение, сильно отличающееся от основной массы значений. Оно является случайным, не характерным для всей генеральной совокупности, но может существенно повлиять на значение выборочного среднего. Поэтому в дополнение к выборочному среднему находят медиану вариационного ряда. Для этого все варианты выписывают в порядке возрастания, повторяя их столько раз, какова их частота. Медиана – это значение варианты, оказавшейся в центре получившейся последовательности. Если ее длина четная, то в центре окажутся два числа, и медиана – это их среднее арифметическое. Если вариационный ряд задан таблицей с частотами для вариант, то центральные числа находятся по их номерам, без выписывания всего ряда в строку. Размах вариационного ряда – это разность между максимальным и минимальным значениями вариант. Пример 1. Дан вариационный ряд 5, 1, 3, 4, 2, 2, 4, 1, 2, 5. Найти его выборочное среднее, моду, медиану, размах. Построить полигон частот. Решение. Объем выборки п = 10. Выборочное среднее
Выпишем значения вариационного ряда в порядке возрастания: 1, 1, 2, 2, 2, 3, 4, 4, 5, 5. Мода равна 2, так как это значение имеет наибольшую частоту, равную 3. Медиана равна
Упражнения 1.1. Дан вариационный ряд а) 8, 11, 10, 11, 13, 10, 9, 11, 10, 9; б) 17, 21, 20, 17, 19, 20, 18, 20, 19;
Найти выборочное среднее, моду, медиану, размах. Построить полигон частот. Точечная оценка параметров Согласно центральной предельной теореме, случайные величины, с которыми приходится иметь дело на практике, распределены по нормальному закону. Этот закон определяется двумя параметрами – математическим ожиданием а и средним квадратичным отклонением σ. Поэтому одна из основных задач статистики – определить значения этих параметров для признака Х в генеральной совокупности. Математическое ожидание для генеральной совокупности объема N – это генеральная средняя. Она вычисляется по формуле
либо по аналогичной формуле с частотами. Среднее квадратичное отклонение определяется через генеральную дисперсию:
Для этих параметров, естественно, напрашиваются оценки, полученные по выборке объема п с помощью аналогичных формул: выборочная средняя
выборочная дисперсия
Но оценки параметров генеральной совокупности должны удовлетворять следующим обязательным требованиям. Несмещенность. Выборочная оценка является случайной величиной. Несмещенностьозначает, что математическое ожидание этой случайной величины должно совпадать с настоящим значением оцениваемого параметра. Это значит, что полученное значение может отличаться от настоящего в ту или другую сторону, но в среднем должно совпадать с ним. Состоятельность. Это значит, что точность оценки можно улучшить, увеличив объем выборки. Кроме этих обязательных требований, есть желательное требование эффективности. Оно означает, что из всех возможных способов получения оценки мы выбираем наиболее эффективный в каком-то смысле: стоимости, затрат времени, и т.п. Можно показать, что оценка генерального среднего посредством выборочного среднего удовлетворяет условиям несмещенности и состоятельности. Но оценка генеральной дисперсии через выборочную дисперсию не является несмещенной: среднее значение ожидается несколько меньше настоящего. Дело в том, что оценка была бы несмещенной, если бы в формуле (2) вместо
Обозначение s 2 связано с тем, что из полученного значения, извлекая квадратный корень, получаем оценку для среднего квадратичного отклонения, обозначаемую через s. Эта оценка является несмещенной и состоятельной. Все вычисления проводятся с помощью специальных расчетных таблиц. Если вариационный ряд задан без указания частоты, то таблица может иметь следующий вид:
В первом столбце стоят номера от 1 до п, во втором исходные выборочные значения, третий столбец вычисляется по ним. В последней строке стоят суммы чисел в соответствующих столбцах. Вычисления производятся по формулам:
Если вариационный ряд задан с частотами вариант, то таблица будет иметь следующий вид:
Если вариационный ряд является интервальным, то будут заданы границы интервалов, и в качестве xi нужно взять середины этих интервалов. Вычисления в последних случаях производятся по тем же формулам (4). Если значения вариант большие, то для облегчения вычислений вводят ложный нуль С. В качестве него обычно берут одно из средних значений вариант. Вычисления тогда оформляют в следующую таблицу:
В этом случае параметры рассчитывают по формулам:
Пример 1. Найти оценки для математического ожидания, дисперсии и среднего квадратичного отклонения некоторой величины по результатам измерений, приведенным в таблице.
Решение. Строим расчетную таблицу
Таблица заполняется в следующем порядке. В первом столбце пишем порядковые номера, второй и третий берем из исходной таблицы. В столбце xi находим середины интервалов. Одно из полученных значений берем в качестве ложного нуля, С = 82,5. Вычисляем три следующих столбца и находим нужные суммы, в частности, п = 84. Далее получаем:
s = Упражнения 2.1. Найти оценки для математического ожидания, дисперсии и среднего квадратичного отклонения для некоторой величины по приведенным результатам измерений: а) 5, 8, 6, 7, 7, 6, 6; б) 172, 193, 201, 177, 190, 203, 185, 194, 191; в)
г)
2.2. Найти оценки для математического ожидания, дисперсии и среднего квадратичного отклонения для распределения роста студентов, взяв в качестве выборки рост студентов вашей группы. Доверительные интервалы Оценки параметров распределения, найденные в предыдущем разделе, являются приближенными. Возникает естественная задача определить, насколько они могут отличаться от настоящих значений. Но точно определить это невозможно, все возможные отклонения носят вероятностный характер. Можно задать интервал около найденной оценки и определить вероятность того, что истинное значение параметра окажется в этом интервале. Понятно, что чем шире интервал, тем больше вероятность попадания в него, то есть тем больше надежность полученного результата. Но если интервал слишком широкий, то сам результат оказывается расплывчатым и, следовательно, мало пригодным для дальнейшего использования. Если же сужать интервал, то понижается надежность результата, то есть увеличивается вероятность ошибки. Улучшить оба этих показателя можно, увеличивая объем выборки. На практике поступают в обратном порядке: задают требуемую надежность результата γ и по этой надежности определяют ширину интервала, в котором искомое значение параметра окажется с вероятностью γ. Этот интервал называется доверительным интерваломс надежностью γ для искомого параметра. Покажем способ нахождения доверительного интервала для математического ожидания а. Рассмотрим сначала случай, когда известно среднее квадратичное отклонение σ. Найденная выборочная оценка
Решение этого уравнения опирается на интегральную теорему Муавра - Лапласа, из которой получается соотношение
где
В итоге получаем следующую последовательность действий. По таблице значений функции Ф(х) находим значение t, для которого Ф(t) = Затем вычисляем искомое δ по формуле
Пример 1. Признак Х распределен нормально с известным σ = 0,75. По выборке объема п = 25 получено значение Решение. Уравнение (1) имеет вид Ф(t) = 0,495. По таблице значений функции Ф(х) находим t = 2,58. Подставляя в формулу (2), получаем
Округляем до 0,01, как в значении (8,32 – 0,39; 8,32 + 0,39) = (7,93; 8,71). Если для генеральной совокупности σ не известно, то границы доверительного интервала окажутся шире, чем в приведенных расчетах. В этом случае δ также вычисляем по формуле (2), но значение t находим по специальной таблице распределения Стьюдента, зависящей от п и γ. В этом случае при п = 100 расхождение с результатом, полученным по формуле (1), составляет 1%; при n > 120 результаты практически совпадают. При уменьшении п расхождение увеличивается. Оно оказывается тем больше, чем выше требуемая надежность γ. Так, расхождение в 20% для γ = 0,95 имеет место при п = 9, для γ = 0,99 при п = 11, для γ = 0,999 при п = 19. Пример 2. Признак Х распределен нормально с неизвестным σ. По выборке объема п = 25 получено значение Решение. По таблице распределения Стьюдента для п = 25 и γ = 0,99 находим t = 2,797. Подставляя в формулу (2), получаем
Получаем доверительный интервал (8,32 – 0,42; 8,32 + 0,42) = (7,90; 8,74). Доверительный интервал для среднего квадратичного отклонения также рассчитывается с помощью специальных таблиц, зависящих от п и γ. Упражнения 3.1. Признак Х распределен нормально с известным σ = 0,5. По выборке объема п = 20 получено значение 3.2. Признак Х распределен нормально с неизвестным σ. По выборке объема п = 20 получено значение 3.3. Найти доверительный интервал для математического ожидания с надежностью γ = 0,95 для роста студентов на основе упражнения 2.2.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1004; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.197.120 (0.011 с.) |

 . Можно показать, что математическое ожидание этой случайной величины равно np, дисперсия npq.
. Можно показать, что математическое ожидание этой случайной величины равно np, дисперсия npq. . Математическое ожидание – это середина отрезка.
. Математическое ожидание – это середина отрезка.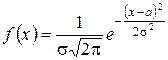 .
.

 .
. и
и  . Какова вероятность: а) хотя бы одного попадания; б) двух попаданий?
. Какова вероятность: а) хотя бы одного попадания; б) двух попаданий?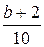 . Найдите вероятность того, что число успехов: а) равно a +10 b +20; б) заключено в пределах от a +10 b +10 до 10 b +25; в) не меньше a +10 b +15.
. Найдите вероятность того, что число успехов: а) равно a +10 b +20; б) заключено в пределах от a +10 b +10 до 10 b +25; в) не меньше a +10 b +15.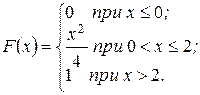
 .
. – это среднее арифметическое всех выборочных значений. Для вариационного ряда x 1, …, xn оно вычисляется по формуле
– это среднее арифметическое всех выборочных значений. Для вариационного ряда x 1, …, xn оно вычисляется по формуле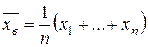 .
. .
. = 2,9.
= 2,9. = 2,5, это среднее арифметическое двух центральных значений. Размах равен 5 – 1 = 4. Полигон частот имеет вид
= 2,5, это среднее арифметическое двух центральных значений. Размах равен 5 – 1 = 4. Полигон частот имеет вид
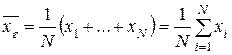 ,
, , где
, где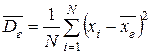 .
. ; (1)
; (1)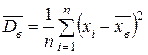 . (2)
. (2) . Но
. Но  . (3)
. (3) ;
; 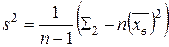 . (4)
. (4) ;
; 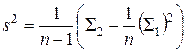 . (5)
. (5) = 86,4;
= 86,4; = 50,2;
= 50,2; = 7,1.
= 7,1.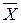 . Доверительный интервал имеет вид (
. Доверительный интервал имеет вид ( . Требуется, чтобы это отклонение не превышало δ с вероятностью γ, это заданная надежность. Эти рассуждения приводят к уравнению
. Требуется, чтобы это отклонение не превышало δ с вероятностью γ, это заданная надежность. Эти рассуждения приводят к уравнению .
. = 2 Ф(t),
= 2 Ф(t), .
.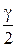 . (1)
. (1)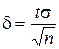 . (2)
. (2) = 0,387.
= 0,387. = 0,42.
= 0,42.


