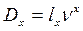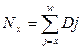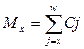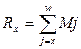Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные принципы страхования – эквивалентности и случайностиСодержание книги
Поиск на нашем сайте Блок 2 1. Основные особенности страхования, отличающие его от других финансовых структур. 2 2. Основные принципы страхования – эквивалентности и случайности. 3 3. Актуарные расчеты. Роль и задачи актуариев страховой компании. 4 4. Виды договоров страхования по способу распределения ответственности за риск. 4 5. Расчет математического ожидания и дисперсии ущерба и возмещения в актуарных расчетах. 6 6. Франшиза. Предназначение. Виды франшиз. 7 7. Основные отличия страхования жизни и страхования иного, чем страхование жизни (нежизни) 8 8. Структура страхового тарифа. Отличительные особенности рисковой премии, нетто-премии, брутто-премии. 8 9. Классификация договоров страхования в зависимости от порядка уплаты страховых премий. 9 10. Актуарные модели – индивидуальные и коллективные. 9 11. Основные подходы к моделированию распределения числа страховых случаев в страховом портфеле. 11 12. Основные подходы к моделированию ущерба при наступлении страхового случая в одном договоре. 14 13. Использование теории полезности в актуарных расчетах. Выбор наиболее выгодного договора с помощью функции полезности. 17 14. Степень риска и ее роль в актуарных расчетах. 18 15. Цели применения перестрахования. Составляющие договора перестрахования. 19 16. Перестрахование факультативное и договорное (облигаторное), пропорциональное и непропорциональное. 20 17. Основные типы договоров пропорционального перестрахования – их сходства и отличия. 23 18. Основные типы договоров непропорционального перестрахования, их сходства и отличия. 24 19. Страховые резервы - причины и цели создания. Особенности расчёта резервов по рисковому страхованию.. 24 20.Построение таблиц смертности. Основные понятия и показатели. 27 21.?????????????. 29 22.?????????????. 29 23. Интенсивность смертности и её связь с функцией дожития. 30 24. Договоры страхования жизни. Классификация по объекту и по предмету страхования. 31 25. Договоры страхования жизни. Классификация по периоду действия страхового покрытия и по форме страхового покрытия. 31 26. Единовременные и периодические нетто-ставки по страхованию на дожитие. 32 27. Единовременные нетто-ставки по пожизненному страхованию на случай смерти. 33 28. Периодические нетто-ставки по пожизненному страхованию на случай смерти. 33 29. Коммутационные числа. 33 30.?????????????. 34
Страхование представляет собой отношения по защите имущественных интересов физических и юридических лиц при наступлении определенных событий (страховых случаев) за счет денежных фондов, формированных из уплаченных или страховых взносов (премий) согласно закону РФ. Актуальность страхования 1. Человек постоянно подвергается тому или иному риску 2. Эти опасности наносят вред личности людей в виде болезней, увечий, смертей; ущерб их дом. хозяйству и.т.д. 3. Вероятность (частота) случ. опасностей и масштабы последствий от них прогрессивно возрастают Основные понятия Страхователь – физ. или юр. лицо, выражающее страховой интерес и вступающее в гражд.-правов. отношения со страховщиком в силу закона или договора. Страховщик – физ. или юр. лицо, проводящее страхование, орг-щее и созд-щее страх. фонда. По форме организации – акционерное страховое общество, общество взаимного страхования, гос. страх. организация Страхователь – отдает свой риск, страховщик – его принимает Плата страхователя за это – цена услуг страховой компании, страховой взнос S – страх. сумма – максимально возм. объем ответственности страховщика по данному риску, указ-ый в договоре страхования С – страх. стоим. – оценка стоимости объекта страхования (как правило, совпадает с рын. ценой объекта) Согласно общим правилам страхования S не м. превышать реальн. стоим. застрах. объекта С: S<=C Х – величина ущерба, наступившего в результате страх. случая Ущерб Х может быть: · фиксированным – когда страх. случай либо наступит с вер-ю Р, и тогда полностью выплатится вся страховая сумма, либо не наступит и выплаты нет · распределенным – когда при наступлении страхового случая величина ущерба Х является случайной величиной с некоторым законом распределения (дискрет. или неприрыв); чтрах. имущества от ущерба У – величина возмещения, выплаченного при наступлении страхового случая согласно условиям договора страхования: У<=min (X,S) Страховой тариф (ставка) – система коэффициентов, на основании которой исчисляется плата за страхование, обычно в % от страх. суммы Брутто-премия (страховая премия) = Страховой тариф * Страховую сумму Страховой платеж – единовременно перечисляемая часть страх. премии · единовременная премия – сумма выплачивается сразу за 1 год · периодическая премия – выплачивается с рассрочкой, некоторой периодичностью, цена договора при этом возрастает, вычисляется с использованием аппарата финансовой математики (ренты пренумерандо, коэффициента дисконтирования) Особенности страхования 1. Страх. фонды образуются на основе перераспределенных денежных доходов и накоплений, образующихся в процессе превышения распределения национального дохода. Это делает страхование особо восприимчивым к тенденциям экономического развития (инфляция, снижение темпов роста экон-ки и т.д.) 2. Для страхования характерна замкнутая раскладка ущерба в рамках созд-го страхового фонда Средства фонда расходятся только для компенсации ущерба его участников. Таким образом, страхование основано на предпосылке, что число страхователей, попавших в страховой случай, существенно меньше числа участников, регулярно выплачивающих страховые взносы в страховой фонд Страхователь имеет право на возмещение только при наступлении страхового события 3. Страхование предусматривает перераспределение или выравнивание ущерба по территории и во времени. Динамика ущерба территориально неравномерна, или не затрагивается в равной мере все территориальные единицы. Это обстоятельство увеличивает возможности раскладки ущербов и расширенные возможности страхования. Неравномерность ущербов во времени порождает необходимость резервирования части страховых платежей для возмещения чрезвычайных ущербов в неблагоприятные годы содержание
Актуарные расчеты. Роль и задачи актуариев страховой компании Актуарные расчеты – процесс, в ходе которого определяются расходы, необходимые на страхование того или иного объекта Основные задачи актуарных расчетов: 1. исчисление и группировка рисков в рамках страховой совокупности 2. оценка частот страховых событий 3. определение распределения ущерба в случае страхового события как по отд. рискам, так и по портфелю в целом 4. обоснование расходов на ведение дела 5. определение величины страх. запаса (капитала), обеспечивающего выживание (неразорение) компании с определенной возможностью 6. анализ возможности повышения устойчивости компании с помощью перестрахования и расчет платы за перестрахование при различных условиях договора в перестраховании. 7. оценка положения страховой компании на страховом рынке и, в зависимости от ситуации, формирование подтверждаемых расчетами рекомендаций по укреплению позиций компании и т.д. Андеррайтинг – процесс изучения возможности страхования определенного риска и возможность принятия этого риска страховой компанией Основная задача актуария – описание и обоснование моделей распределения, используемых для аппроксимации числа страховых случаев в договоре. содержание Методы страхования В договоре частичного страхования необходимо учитывать 2 момента: 1. Необходимо рассчитать (оценить) параметры нового распределения, указанного снизу в случае условной франшизы и сверху по договорам 1 порядка, указанного и уменьшенного на сумму франшизы в случае безусловной франшизы 2. кроме того, при использовании франшизы, поскольку по части страховых случаев, убыток в которых не превысил L, страховщик не выплачивает возмещение, вер-ть выплаты по страховому случаю уменьшается. Также изменится и распределение числа исков. содержание Индивидуальная модель Предпосылкой к использованию моделей этого типа является однородность групп рисков, то есть риски отдельных групп должны быть схожи во всём за исключением страховых сумм. Это обременительное условие, которое редко выполняется на практике При выполнении указанного условия, распределение совокупного годового убытка группы рисков можно вычислить как свёртку распределений годовых убытков отдельных рисков. Для простоты вычисления свёртки предпочтение отдаётся более «простым» распределениям; а именно распределениям, обладающим следующими свойствами: 1) функция плотности выписывается явно, а не задаётся при помощи интеграла 2) модель содержит небольшое число параметров Наиболее часто используются гамма, обратное гауссовское и логнормальное распределения. Напомним, что условие, лежащее в основе индивидуальной модели, является обременительным. В некотором смысле, такая модель не воспринимается всерьёз. Они используется лишь как составная часть других моделей. Основным предназначением индивидуальной модели является расчёт характеристик совокупного годового убытка группы рисков (математическое ожидание и дисперсия) с целью расчёта тарифов. Коллективная модель Вкратце суть подхода заключается в рассмотрении портфеля как производителя убытков, не учитывая принадлежность убытков конкретным рискам. Распределение убытка строится на основе распределений убытков и размера убытков в одном страховом случае, при этом плоскость отдельных рисков не задействуется. Очевидно, что при таком подходе происходит потеря информации. Однако следует отметить, что эта потеря информации не отражается на качестве результата, так как распределения коллективной модели (распределения числа убытков и размеров убытков) могут быть вычислены с очень высокой степенью точности. Следует отметить, что при помощи коллективной модели можно решать важные практические задачи (получение представления о вероятности любого размера убытка, моделирование хвоста распределения совокупного убытка), в то время как индивидуальная модель полезна лишь как составная часть других моделей. При использовании коллективной модели предполагается, что размеры убытков в отдельных страховых случаях: 1) независимы 2) одинаково распределены 3) не зависят от числа убытков в интересующем временном интервале содержание Построение таблиц смертности. Основные понятия и показатели. Таблицы смертности представляют собой систематизированный набор статистических данных о продолжительности жизни населения данной страны или выделенной его группы. Выделение групп может проводиться по разным признакам: по полу, региону, профессии и т.п. Во всех случаях таблицы смертности содержат «упорядоченный ряд взаимосвязанных величин, показывающих уменьшение с возрастом вследствие смертности некоторой совокупности родившихся, а также показателей, характеризующих уровень смертности для различных периодов жизни данной совокупности». Таблицы смертности также называют таблицами продолжительности жизни. В общих таблицах возраст является единственным определяющим параметром (входом таблицы). Общие таблицы дают представление о динамике демографических процессов для всего населения в целом. В специальных таблицах, кроме возраста, учитывается ряд других параметров. Такие таблицы называются таблицами с отбором, или селективными. В полных ТС показатели даны по возрастам с интервалом в 1 год, в кратких таблицах – с интервалом 5 и 10 лет. ТС могут начинаться с нулевого возраста или же с некоторого данного возраста. ТС представляет собой набор столбцов, соответствующих различным демографическим показателям. Элементы столбцов упорядочены по возрасту. Первым в ТС, как правило, приводится число людей, доживающих до возраста х: lx. Это число относится к фиксированному числу родившихся, обозначаемому l0 и называемому корнем таблицы смертности. Обычные значения для l0: 1 млн., 10 или 100 тыс., но оно может быть и произвольным числом. Таким образом, если l0 = 100000 число родившихся, то l1 = 98729 означает, что лишь 98729 из них доживут до своего первого дня рождения. ТС заканчиваются строкой, соответствующей предельному возрасту ω. Другой важной характеристикой, встречающейся в таблицах смертности, является величина dx, представляющая число умерших в промежутке между годами х и х +1 своей жизни. Таким образом dx – это число умерших в возрасте х. Очевидно, что lx = lx+1 + dx, т.к. среди достигших возраста х каждый из них либо достигнет возраста х +1, либо умрет в течение одного года. Эта формула м.б. переписана в виде: lx+1 = lx – dx. Число qx можно рассматривать как вероятность умереть в течение одного года (после дня рождения) для человека, достигшего возраста х. Более точно следовало бы говорить, что число qx (из таблицы смертности) является статистической оценкой этой вероятности. Число qx называют также уровнем смертности в возрасте х. Таким образом, qx = dx / lx. Дополнение qx до 1, т.е. число px = 1 – qx равно доле тех из lx, достигших возраста х, что доживут до возраста х +1. Эта величина представляет собой условную вероятность прожить еще один год по достижении возраста х. Поскольку qx = dx / lx, то px = 1 – qx = 1 – dx / lx = (lx – dx) / lx = lx +1 / lx, т.е. px = lx+1 / lx. Соответственно, можно записать: lx+1 = lx ∙ px или lx = lx+1 / px= dx / qx. Аналогично: dx = lx ∙ qx Введем еще ряд вероятностных характеристик, относящихся к более продолжительным периодам. Число npx = lx+n / lx равно вероятности прожить еще n лет для лица, достигшего возраста х. Соответственно число nqx = 1 – npx = ndx / lx равно вероятности умереть в течение следующих n лет для лица, достигшего возраста х. Для вероятностей npx выполнены очевидные соотношения: 2px = px ∙ px+1.; 3 px = px ∙ px +1 ∙ px +2. Имеется много методов построения таблиц смертности. Основное различие этих методов состоит в выборе базового показателя, на основании которого вычисляются все остальные. Чаще всего в качестве базового показателя берется qx, т.е. вероятность смерти в течение года после достижения возраста х. Этот показатель оценивается исходя из имеющихся статистических данных. Оценив qx, можно получить все остальные показатели. Рассмотрим подлежащее и сказуемое таблицы смертности. Подлежащим ТС будет возраст Возрастной интервал берётся от 1 до 100 лет (т.е. 1. вероятность умереть в данном возрасте 2. Число умирающих в данном возрастном интервале 3. Число доживающих до данного возраста 4. Функция дожития
Если же исходными являются не вероятности смерти qx, а вероятности дожития рx, то ряд значений для lx можно получить по формулам lx+1 = lx*px; dx = lx-lx+1 для α ≤ х ≤ ω. Вычисленные значения округляются, как правило, до ближайшего целого числа. Иногда, особенно при построении специальных таблиц, корень таблицы помещается в “середину”, то есть значения α и lα относятся к “промежуточным”. В этом случае процесс вычисления идет в двух направлениях: к младшим и старшим возрастам. При этом значения lx и dx для старших возрастов получаются по формулам, приведенным выше, а для младших возрастов применяются формулы: lx-1 = lx/ px-1; dx-1 = lx-1 - lx если исходный показатель px. Если же в качестве исходного взят qx, то получив сначала px = 1 – qx, применяют формулы, приведенные выше. Таким образом, центральным моментом при построении таблиц смертности на основе показателей qx или px является получение их оценки на основании статистических данных. При использовании прямого метода эта оценка строится непосредственно на определении этих вероятностей, например, для qx по формуле: qx = dx / lx. Однако непосредственное применение прямого метода наталкивается на значительные трудности. Дело в том, что по самому смыслу этих и других показателей таблицы смертности они относятся к некоторой заданной совокупности лиц, родившихся в одном и том же году. Такие совокупности, образование которых связано с некоторым демографическим событием (рождением, браком и тп.), в демографии называют когортами. Получение демографических показателей для реального поколения получило в демографии название когортного метода, или продольного анализа. Коммутационные функции (см вопрос 29)
содержание 21.????????????? содержание 22.????????????? содержание Коммутационные числа Для упрощения расчетов тарифных ставок и резервов в контрактах по СЖ вводятся упрощающие функции – КОММУТАЦИОННЫЕ функции. Все эти функции делятся на 2 группы: - для доживающих -для умерших. Обязательным эл-том явл дисконтный мн-ль: Основные коммутационные функции: (см вопрос 20) 1. Дисконтированные числа доживающих до возраста Х: 2. Сумма дисконтированных чисел всех доживающих и переживающих возраст х лет: 3. Сумма чисел: 4. Дисконтированные числа умирающих в возрасте х лет: 5. Сумма дисконтированных чисел умирающих в возрасте х лет и выше: 6. Dx, Nx, Sx выбраны для обозначения тк в простейших формулах страхования числа Dx играют роль знаменателя, числа Nx – числителя, а Sx-сумма Nx. Сx, Mx, Rx – ближайшие по алфавиту. Коммутационная функция строится из заданной ТС и при зажанной %-ой ставке. Коммутац функции играли большую роль в докомпьютерную эпоху, тк значительно сокращали объем вычислений. Западные актуарии доказали, что исп-ие коммутац функций приводит к несколько завышенным тарифам (около 1%). Коммутац функции – технические показатели, не имеющие содержательного смысла. Они лишь опред образом связывают показатели ТС и дисконтирующие мн-ли. Что бы перевести в комутацион числа логические формулы (те, что записываются через интегралы) для расчета единоврем нетто-ставки: 1. записывается общая формула 2. числитель и знаменатель домножается на 3. Это выражение записывается через коммутац числа. содержание
30.????????????? содержание Блок 2 1. Основные особенности страхования, отличающие его от других финансовых структур. 2 2. Основные принципы страхования – эквивалентности и случайности. 3 3. Актуарные расчеты. Роль и задачи актуариев страховой компании. 4 4. Виды договоров страхования по способу распределения ответственности за риск. 4 5. Расчет математического ожидания и дисперсии ущерба и возмещения в актуарных расчетах. 6 6. Франшиза. Предназначение. Виды франшиз. 7 7. Основные отличия страхования жизни и страхования иного, чем страхование жизни (нежизни) 8 8. Структура страхового тарифа. Отличительные особенности рисковой премии, нетто-премии, брутто-премии. 8 9. Классификация договоров страхования в зависимости от порядка уплаты страховых премий. 9 10. Актуарные модели – индивидуальные и коллективные. 9 11. Основные подходы к моделированию распределения числа страховых случаев в страховом портфеле. 11 12. Основные подходы к моделированию ущерба при наступлении страхового случая в одном договоре. 14 13. Использование теории полезности в актуарных расчетах. Выбор наиболее выгодного договора с помощью функции полезности. 17 14. Степень риска и ее роль в актуарных расчетах. 18 15. Цели применения перестрахования. Составляющие договора перестрахования. 19 16. Перестрахование факультативное и договорное (облигаторное), пропорциональное и непропорциональное. 20 17. Основные типы договоров пропорционального перестрахования – их сходства и отличия. 23 18. Основные типы договоров непропорционального перестрахования, их сходства и отличия. 24 19. Страховые резервы - причины и цели создания. Особенности расчёта резервов по рисковому страхованию.. 24 20.Построение таблиц смертности. Основные понятия и показатели. 27 21.?????????????. 29 22.?????????????. 29 23. Интенсивность смертности и её связь с функцией дожития. 30 24. Договоры страхования жизни. Классификация по объекту и по предмету страхования. 31 25. Договоры страхования жизни. Классификация по периоду действия страхового покрытия и по форме страхового покрытия. 31 26. Единовременные и периодические нетто-ставки по страхованию на дожитие. 32 27. Единовременные нетто-ставки по пожизненному страхованию на случай смерти. 33 28. Периодические нетто-ставки по пожизненному страхованию на случай смерти. 33 29. Коммутационные числа. 33 30.?????????????. 34
Страхование представляет собой отношения по защите имущественных интересов физических и юридических лиц при наступлении определенных событий (страховых случаев) за счет денежных фондов, формированных из уплаченных или страховых взносов (премий) согласно закону РФ. Актуальность страхования 1. Человек постоянно подвергается тому или иному риску 2. Эти опасности наносят вред личности людей в виде болезней, увечий, смертей; ущерб их дом. хозяйству и.т.д. 3. Вероятность (частота) случ. опасностей и масштабы последствий от них прогрессивно возрастают Основные понятия Страхователь – физ. или юр. лицо, выражающее страховой интерес и вступающее в гражд.-правов. отношения со страховщиком в силу закона или договора. Страховщик – физ. или юр. лицо, проводящее страхование, орг-щее и созд-щее страх. фонда. По форме организации – акционерное страховое общество, общество взаимного страхования, гос. страх. организация Страхователь – отдает свой риск, страховщик – его принимает Плата страхователя за это – цена услуг страховой компании, страховой взнос S – страх. сумма – максимально возм. объем ответственности страховщика по данному риску, указ-ый в договоре страхования С – страх. стоим. – оценка стоимости объекта страхования (как правило, совпадает с рын. ценой объекта) Согласно общим правилам страхования S не м. превышать реальн. стоим. застрах. объекта С: S<=C Х – величина ущерба, наступившего в результате страх. случая Ущерб Х может быть: · фиксированным – когда страх. случай либо наступит с вер-ю Р, и тогда полностью выплатится вся страховая сумма, либо не наступит и выплаты нет · распределенным – когда при наступлении страхового случая величина ущерба Х является случайной величиной с некоторым законом распределения (дискрет. или неприрыв); чтрах. имущества от ущерба У – величина возмещения, выплаченного при наступлении страхового случая согласно условиям договора страхования: У<=min (X,S) Страховой тариф (ставка) – система коэффициентов, на основании которой исчисляется плата за страхование, обычно в % от страх. суммы Брутто-премия (страховая премия) = Страховой тариф * Страховую сумму Страховой платеж – единовременно перечисляемая часть страх. премии · единовременная премия – сумма выплачивается сразу за 1 год · периодическая премия – выплачивается с рассрочкой, некоторой периодичностью, цена договора при этом возрастает, вычисляется с использованием аппарата финансовой математики (ренты пренумерандо, коэффициента дисконтирования) Особенности страхования 1. Страх. фонды образуются на основе перераспределенных денежных доходов и накоплений, образующихся в процессе превышения распределения национального дохода. Это делает страхование особо восприимчивым к тенденциям экономического развития (инфляция, снижение темпов роста экон-ки и т.д.) 2. Для страхования характерна замкнутая раскладка ущерба в рамках созд-го страхового фонда Средства фонда расходятся только для компенсации ущерба его участников. Таким образом, страхование основано на предпосылке, что число страхователей, попавших в страховой случай, существенно меньше числа участников, регулярно выплачивающих страховые взносы в страховой фонд Страхователь имеет право на возмещение только при наступлении страхового события 3. Страхование предусматривает перераспределение или выравнивание ущерба по территории и во времени. Динамика ущерба территориально неравномерна, или не затрагивается в равной мере все территориальные единицы. Это обстоятельство увеличивает возможности раскладки ущербов и расширенные возможности страхования. Неравномерность ущербов во времени порождает необходимость резервирования части страховых платежей для возмещения чрезвычайных ущербов в неблагоприятные годы содержание
Основные принципы страхования – эквивалентности и случайности 1. Принцип эквивалентности (коллективный баланс) Страхование основывается на том, что коллектив (портфель, объединение) нескольких рисков имеет более выгодное распределение убытков и размер премии (в расчете на один полис), чем каждый отдельный риск, поскольку в коллективе благоприятные и неблагоприятные (по сравнению с математическим ожиданием риска) процессы убытков отдельных рисков могут взаимно компенсироваться. Принцип эквивалентности обязательств страховщика и страхователя математически выражается в равенстве мат. ожидания двух величин: суммы всех страховых взносов и суммы всех страховых возмещений. Именно из этого условия определяется размер осн. сост-ей страховой премии – рисковой премии. Страховая эквивалентность состоит в том, что в конечном счете все взносы (за исключением части страх. премии, предназначенной на ведение дела и прибыль – нагрузки), получаемые страх. компанией (СК) от клиентов за тарифный период (например, на 5 лет), вернутся к страховщикам в виде страховых выплат, т.е. требование равновесия между доходами и расходами страховой компании. Риск угрожает многим лицам, но не многие попадут в страховой случай. Теоретической базой для главного принципа страхования – принципа эквивалентности служит один из фундаментальных законов теории вероятностей – закон больших чисел При достаточно большом числе n независимых случайных величин, дисперсии которых ограничены некоторым числом, среднее арифметическое этих величин стремится по вероятности к среднему арифметическому их мат. ожиданий
Если говорить об однородных рисках с одинаковым математическим ожиданием М(х), то среднее арифметическое всех рисков стремится по вероятности к мат. ожиданию ущерба по данному. виду страх. договора.
Таким образом, согласно закону больших чисел: 1. Мат. ожидание ущерба в одном договоре – справедливая цена за принятие такого рода случайных рисков, поэтому риск. премию (РП) вычисляют как мат. ожидание ущерба 2) Требует собрать как можно большую группу независимых однородных рисков За исключительно важную роль для коллективного баланса и исчисления страховых премий закон больших чисел часто называют фундаментальным законом страхования 2.Принцип случайности Страховаться могут только те события, которые обладают признаками вероятности и случайности их наступления. Страховой риск – это случайное событие (или их совокупность) на случай наступление которого проводится страхование Риски: · чистые (связаны со случайными событиями, которые влекут за собой или только ущерб, или ост-т ситуацию неизменной) · спекулятивные (предполагают возможность извлечения прибыли) Страхуются только чистые риски!!! Критерии стахуемости риска 1. Должен быть случайный характер ущерба (непредсказуемость наступления и по времени и по величине) 2. возможность оценки распределения ущерба (должна быть количественная характеристика вероятности и распределения ущерба) 3. однозначность распределения ущерба (т.е. объекты страхования и возмещение ущерба должны быть определены предельно точно); 4. независимость страхования распределений друг от друга (страховщик должен избегать так называемых кумулятивных рисков, когда одно страх. событие может привести к ущербам по множеством других договорах страхования 5. оценка максимально возможной величины страхования ущерба: 6. относительно небольшая вероятность наступления страхового случая содержание
|
||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 335; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.017 с.) |

 ). Сказуемое таблицы состоит из множества граф, опишем каждую из них в отдельности.
). Сказуемое таблицы состоит из множества граф, опишем каждую из них в отдельности. . Рассчитывается на основе реальных (отчётных или официальных) данных и является основой таблицы.
. Рассчитывается на основе реальных (отчётных или официальных) данных и является основой таблицы.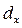 , рассчитывается как dx=lx*qx.
, рассчитывается как dx=lx*qx. . Первоначальное значение
. Первоначальное значение  берётся равное 100000 (или10000), а последующие значения рассчитываются по формуле lx+1 = lx-dx .
берётся равное 100000 (или10000), а последующие значения рассчитываются по формуле lx+1 = lx-dx . , означающая долю лиц из совокупности, доживающих до возраста х [
, означающая долю лиц из совокупности, доживающих до возраста х [ 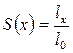 ]. 5.
]. 5.  - округленная продолжительность жизни в возрасте х лет [
- округленная продолжительность жизни в возрасте х лет [  ].
]. - средняя продолжительность жизни, равная
- средняя продолжительность жизни, равная  или
или  .
.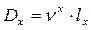 .
.  .
.  .
. .
. .
. .;
.; 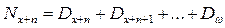 .;
.; 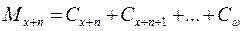 .
. .
.