Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция распределения случайной величины.
Для непрерывных случайных величин применяют такую форму закона распределения, как функция распределения. Функция распределения случайной величины Х, называется функцией аргумента х, что случайная величина Х принимает любое значение меньшее х (Х<х) F(х)=Р(Х<х) F(х) - иногда называют интегральной функцией распределения или интегральным законом распределения. Функция распределения обладает следующими свойствами: 1. 0<F(х)<1 2. если х1>х2,то F(х1)>F(х2) 3. функция может быть изображена в виде графика. Для непрерывной величины это будет кривая изменяющееся в пределах от 0 до 1, а для дискретной величины - ступенчатая фигура со скачками. С помощью функции распределения легко находится вероятность попадания величины на участок от α до β Р(α<х<β) рассмотрим 3 события А - α<Х В - α<Х<β С - Х<β С=А+В Р(С)=Р(А)+Р(В) Р(α<х<β)=Р(α)-Р(β) Плотность распределения вероятности непрерывной случайной величины. Плотность распределения вероятности непрерывной случайной величины Х называется функция f(х) равная первой производной от функции распределения F(х) График плотности распределения называется кривой распределения. Основные свойства плотности функции распределения: 1. f(х)>0 2. Характеристики положения случайной величины. Модой (Мо) случайной величины х называется наиболее вероятное ее значение. Это определение строго относится к дискретным случайным величинам. Для непрерывной величины модой называется такое ее значение для которого ф-ция плотности распределения имеет максимальную величину. Медианой (Ме) случайной величины называется такое ее значение для которого окажется ли случайная величина меньше этого значения. Для непрерывной случайной величины медиана это абсцисса точки в которой площадь под кривой распределяется пополам. Для дискретной случайной величины значение медианы зависит от того четное или нечетное значение случайной величины n=2k+1, то Ме=хк+1 (среднее по порядку значение) Если значение случайных величин четное, т.е n=2k, то Математическое ожидание случайной величины. Математическим ожиданием случайной величины х (M[x])называется средне взвешенно значение случайной величины причем в качестве весов выступают вероятности появления тех или иных значений.
Для дискретной случайной величины
Для непрерывной
С механической точки зрения мат. Ожидание это абсцисса центра тяжести системы точек расположенных по одноименной оси. Размерность мат. Ожидания совпадает с размерностью самой случайной величины. Математическое ожидание случайной величины всегда больше наименьшего значения и меньше наибольшего.
Характеристики рассеяния. Дисперсия Дисперсия (D[x]) характеризует рассеивание или разряженность случайной величины около ее математического ожидания. Для дискретных Для непрерывных
Дисперсия случайной величины всегда величина положительная Размерность дисперсии равна квадрату разности случайной величины Среднеквадратическое (стандартное) отклонение.
Некоторые законы распределения случайных величин. Для дискретных случайных величин - биномиальное распределение и распределение Пуассона Для непрерывных - равномерное показательное, экспоненциальное и нормальное распределение. Биномиальное распределение. Биномиальным называют законы распределения случайной величины Х числа появления некоторого события в n опытах если вероятность р появления события в каждом опыте постоянна
Сумма вероятностей представляют собой бином Ньютона
Для определения числовых характеристик в биномиальное распределение подставить вероятность которая определяется по формуле Бернули.
При биномиальном распределении дисперсия равна мат. Ожиданию умноженному на вероятность появления события в отдельном опыте. Распределение Пуассона Когда требуется спрогнозировать ожидаемую очередь и разумно сбалансировать число и производительность точек обслуживания и время ожидания в очереди. Пуассоновским называют закон распределения дискретной случайной величины Х числа появления некоторого события в n-независимых опытах если вероятность того, что событие появится ровно m раз определяется по формуле.
n-число проведенных опытов р-вероятность появления события в каждом опыте В теории массового обслуживания параметр пуассоновского распределения определяется по формуле
а=λt, где λ - интенсивность потока сообщений t-время Необходимо отметить, что пуассоновское распределение является предельным случаем биномиального, когда испытаний стремится к бесконечности, а вероятность появления события в каждом опыте стремится к 0.
Пуассоновское распределение является единичным распределением для которого такие характеристики как мат. Ожидание и дисперсия совпадают и они равны параметру этого закона распределения а. Закон равномерной плотности Равномерным называется распределение непрерывной случайной величины Х все значения которой лежат на отрезке [a;b] и имеют при этом постоянную плотность распределения
площадь под кривой распределения равна 1 и поэтому с(в-а)=1
вероятность попадания случайной величины Х на интервал от (α;β)
α=а, если α<а β=в, если β>в основные числовые характеристики закона распределения плотности вычисляются по общим формулам и они равны
|
||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 225; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.37.123 (0.01 с.) |








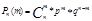



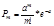 a=np
a=np