
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория вероятностей и математическая статистика. Случайные и достоверные события.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение и основные свойства вероятности. Аксиоматическое определение вероятности. Пусть задано пространство элементарных событий Е и каждому событию А
Тогда говорят, что на событиях в множестве Е задана вероятность, а число Р (А) называется вероятностью события А.
Классическое определение вероятности. Пусть пространство элементарных событий Е состоит из N равновозможных элементарных событий, среди которых имеется n событий, благоприятствующих событию А, тогда число
Р (А) = n / N
называется вероятностью события А. Основные свойства вероятности. Пусть задано пространство элементарных событий Е, а вероятности Р определены на событиях из Е. Тогда:
Основные формулы комбинаторики 1. Размещения с повторениями. Определение. Кортежами длины k составленные из элементов m – элементного множества X называют размещениями с повторениями из m элементов по k. Число этих кортежей обозначают
Пример. Сколько пятизначных номеров можно составить из 9 цифр 1,2,3,4,5,6,7,8,9? Решение. Такие номера являются кортежами длины 5, составленными из элементов множества X = {1,2,3,4,5,6,7,8,9}. По формуле (8) их число равно 2. Размещения без повторений. Определение Упорядоченное множество длины k составленное из элементов m – элементарного множества X называют размещениями без повторений из m элементов множества X по k и обозначают
Пример. Сколькими способами можно выбрать из группы, состоящей из 40 студентов старосту, профорга, физорга. Решение. Любой такой выбор является размещением без повторений из 40 элементов по 3.
3. Перестановки без повторений. Определение. Перестановками без повторений из m элементов называют размещения без повторений из этих элементов по m. Число перестановок из m элементов обозначают
4. Сочетания без повторений Определение. Будем строить из элементов множества X не кортежи, а подмножества. k – элементные подмножества m – элементного множества X называют сочетаниями без повторений из элементов этого множества по k. Их число обозначают
Пример. Сколькими способами можно составить команду по бегу из четырех человек для соревнования по бегу если имеется 7 бегунов? Решение.
Так как площадь области g равна площади квадрата G без суммы двух угловых (незашрихованных) треугольников. Теорема об умножении вероятностей. Теорема. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: Р (АВ) = Р (А) РA (В). (*)
Доказательство З а м е ч ан и е. Применив формулу (*) к событию ВА, получим Р (ВА) = Р (В) РB (А), или, поскольку событие ВА не отличается от события АВ, Р(АВ) = Р (В) РB (А). (**)
Сравнивая формулы (*) и (**), заключаем о справедливости равенства Р (А) РA (В) = Р (В) РB (А). (***) С л е д с т в и е. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:
Р (AВС) = Р (А) РA (В) РAB (С).
Заметим, что порядок, в котором расположены события, может быть выбран любым, т. е. безразлично какое событие считать первым, вторым и т. д. Формула полной вероятности Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также вероятностей этих гипотез. Пусть дано вероятностное пространство 1. 2. 3. Пусть
Формула полной вероятности также имеет следующую интерпретацию. Пусть
Тогда
т.е. априорная вероятность события равна среднему его апостериорной вероятности. Формула Байеса Пусть
Доказательство. По определению условной вероятности,
Пример. Три организации представили в контрольное управление счета для выборочной проверки. Первая организация представила 15 счетов, вторая — 10, третья — 25. Вероятности правильного оформления счетов у этих организаций известны и соответственно равны: 0,9; 0,8; 0,85. Был выбран один счет и он оказался правильным. Определить вероятность того, что этот счет принадлежит второй организации. Решение. Пусть
По формуле полной вероятности определяем вероятность выбора правильно оформленного счета
По формуле Байеса находим исходную вероятность
Свойства дисперсии 1. Дисперсия постоянной величины равна нулю: D(c)=0. 2. Постоянный множитель можно вынести из-под знака дисперсии, возведя его в квадрат: D(k*X)= k2D(X). 3. Если случайные величины X и Y независимы, то дисперсия суммы равна сумме дисперсий: D(X+Y)=D(X)+D(Y). 4. Для дисперсии справедлива вычислительная формула: ПРИМЕР. Известны математические ожидания и дисперсии двух независимых случайных величин X и Y: M(x)=8, M(Y)=7, D(X)=9, D(Y)=6. Найти математическое ожидание и дисперсию случайное величины Z=9X-8Y+7. Математическое ожидание Mx случайной величины x равно
Теория вероятностей и математическая статистика. Случайные и достоверные события. Тео́рия вероя́тностей — раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними. Теория вероятностей изучает математические законы распределения случайных событий, и фактически является теоретической базой для математической статистики. Но, если в теории вероятностей обычно распределение задано тем или иным образом, и требуется найти вероятности, числовые характеристики (например, математическое ожидание, дисперсию и т.п.), построить графики функции и плотности распределения, то в задачах математической статистики, напротив, известны данные (выборка), собранные по результатам какого-то эксперимента или наблюдения, по которым следует определить закон распределения, наиболее подходящий в данном случае, достоверную с некоторой долей вероятности информацию о том, какими могут быть математическое ожидание или среднеквадратическое отклонение величины и т.п. математическая статистика - это раздел математики, который изучеет методы сбора, систематизации, обработки и использования статистических данных для получения научно обоснованных выводов и принятия на их основе решений. Почему же для обработки простых наборов данных требуется целая наука? Потом, что эти данные, как бы мы не старались, никогда не являются точными, содержат случайные ошибки. Это могут быть и погрешности измерительных приборов, и ошибки человеческие (связанные с тем, кто проводит исследование и измерение), и неоднородность данных или, конечно, их недостаточность (невозможно изучить, например, всех коров в мире, чтобы делать выводы об их удоях;), или опросить всех избирателей чтобы сделать прогноз выигрыша для кандидата на выборах). Обычно исследователь многократно повторяет (если это физически возможно) свой опыт, получая большое количество однотипных данных, которые теперь надо обработать и сделать весомые выводы, которые позволят не только продвинуться глубже в изучении предмета (будь то удои коров или политические предпочтения), но и сделать выводы, прогнозы, принять важные экономические решения и т.д. В математике существует наука, которая изучает объекты, связанные с понятиями случайности и вероятности. Теория вероятностей есть математическая наука, изучающая закономерности в случайных явлениях. Случайное явление (событие) – это такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по-иному. Математические законы теории вероятностей являются отражением реальных статистических законов, объективно существующих в массовых случайных явлениях природы, к изучению которых теория вероятностей применяет математические методы и по своему методу является одним из разделов математики. Осуществление каждого отдельного наблюдения, опыта или измерения при изучении эксперимента называют испытанием. Результат испытания называется событием. Различают события: достоверные, невозможные и случайные. События обозначаются большими латинскими буквами А, В, С,..., невозможное – Æ, достоверное – W. Достоверное событие – это такое событие, которое всегда происходит в рассматриваемом эксперименте (содержит все точки множества W). Невозможное событие – это такое событие, которое никогда не происходит в рассматриваемом эксперименте (пустое множество Æ). Примеры: если в урне все шары белые, то достать белый шар является достоверным событием, а достать черный шар является невозможным событием; если человек прыгнул в воду, то выйти мокрым является достоверным событием, а выйти сухим является невозможным событием. Случайное событие – это такое событие, которое при воспроизведении опыта может наступить, а может и не наступить. Пример. Брошена монета. Выпал герб. Это событие случайное, так как могла выпасть другая сторона монеты. Кроме того события могут быть совместными и несовместными, зависимыми или независимыми. Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании. Случайные события А и В называется несовместными, если при данном испытании появление одного из них исключает появление другого события. Примеры: совместные события: идет дождь и идет снег, человек ест и человек читает, число целое и четное; несовместные события: день и ночь, студент одновременно едет на занятие и сдает экзамен, число иррациональное и четное. Событие А называется независимым от события В, если вероятность появления события А не зависит от того произошло событие В или нет. Событие А называется зависимыми от события В, если вероятность появления события А зависит от того произошло или не произошло событие В. Примеры: два студент одновременно сдают экзамен независимо друг от друга, работник получит оплату труда в зависимости от качества ее выполнения. Равновозможные события – это такие события, которые имеют одинаковые возможности для их появления. Полная группа событий - это совокупность единственно возможных событий при данном испытании. Пример: студент может сдать экзамен на любую оценку: студент может сдать экзамен на 5, студент может сдать экзамен на 4, студент может сдать экзамен на 3. Противоположные события; Два случайные события А и В называется противоположными, если они несовместны и образуют полную группа событий. Примеры: студент может сдать экзамен или не сдать, день и ночь. Конкретный результат испытания называется элементарным событием. Совокупность всех возможных, различных, конкретных исходов испытаний называется множеством элементарных событий. Сложным событием (исходом) называется произвольное подмножество множества элементарных событий. Сложное событие в результате испытания наступает тогда и только тогда, когда в результате испытаний произошло элементарное событие, принадлежащее сложному. Например, испытание - подбрасывание кубика. Элементарное событие - выпадение грани с числом «1». Сложное событие - выпадение грани с нечетным числом. 2. Основные определения теории вероятностей Теория вероятности – это наука, которая изучает закономерности, порожденные случайными событиями. Педагогические явления относятся к числу массовых: они охватывают большие совокупности людей, повторяются из года в год, совершаются непрерывно. Показатели (параметры, результаты) педагогического процесса имеют вероятностный характер: одно и то же педагогическое воздействие может приводить к различным следствиям (случайные события, случайным величинам). Тем не менее, при многократном воспроизведении условий определенные следствия появляются чаще других, - это и есть проявление так называемых статистических закономерностей (изучением которых занимаются теория вероятностей и математическая статистика). Случайная величина (СВ) – это численная характеристика, измеряемая по ходу опыта и зависящая от случайного исхода. СВ реализуемая по ходу опыта и сама является случайной. Каждая СВ задает распределение вероятностей. Основным свойством педагогических процессов, явлений служит их вероятностный характер (при данных условиях они могут произойти, реализоваться, но могут и не произойти). Для таких явлений существенную роль играет понятие вероятности. Вероятность (Р) показывает степень возможности осуществления данного события, явления, результата. Вероятность невозможного события равна нулю p = 0, достоверного — единице p = 1 (100%). Вероятность любого события лежит в пределах от 0 до 1, в зависимости от того, насколько это событие случайно. Если мы интересуемся событием A, то, скорее всего, можем наблюдать, фиксировать факты его появления. Потребность в понятии вероятности и ее вычисления возникнет, очевидно, только тогда, когда мы наблюдаем это событие не каждый раз, либо осознаем, что оно может произойти, а может не произойти. И в том и другом случае полезно использовать понятие частоты появления события f(A) - как отношения числа случаев его появления (благоприятных исходов) к общему числу наблюдений. Частота наступления случайного события зависит не только от степени случайности самого события, но и от числа (количества) наблюдений за этой СВ. Существует два вида выборок СВ: зависимые и независимые. Если результаты измерения некоторого свойства у объектов первой выборки не оказывают влияния на результаты измерения этого свойства у объектов второй выборки, то такие выборки считаются независимыми. В тех случаях, когда результаты одной выборки влияют на результаты другой выборки, выборки считаютзависимыми. Классический способ получения зависимых измерений – это двукратное измерение одного и того же свойства (или разных свойств) у членов одной и той же группы. Событие А не зависит от события В, если вероятность события А не зависит от того произошло или нет событие В. События А и В независимы, если Р(АВ)=Р(А)Р(В). На практике независимость события устанавливается из условий опыта, интуиции исследователя и практики. СВ бывает дискретной (мы можем пронумеровать ее возможные значения), например, выпадение игральной кости = 4, 6, 2, и непрерывной (ее функция распределения F(x) – непрерывна), например, время службы лампочки. Математическое ожидание – числовая характеристика СВ, приближенно равная среднему значению СВ: M(x)=x1p1+x2p2+…+xnpn
|
|||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 621; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.015 с.) |

 Е поставлено в соответствие единственное число Р (А) такое, что:
Е поставлено в соответствие единственное число Р (А) такое, что:

 (букваA от французского слова arrangement – размещение. Черта сверху указывает на возможность повторения элементов).
(букваA от французского слова arrangement – размещение. Черта сверху указывает на возможность повторения элементов). . (8)
. (8) .
. . Число размещений без повторений изm элементов по k находится по формуле
. Число размещений без повторений изm элементов по k находится по формуле . (9)
. (9) .
. от французского словаpermutation – перестановка и находятся по формуле
от французского словаpermutation – перестановка и находятся по формуле . (10)
. (10) . От французского словаcombination – комбинация.
. От французского словаcombination – комбинация. . (11)
. (11)


 , и полная группа попарно несовместных событий
, и полная группа попарно несовместных событий 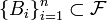 , таких что
, таких что

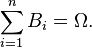
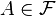 — интересующее нас событие. Тогда
— интересующее нас событие. Тогда .
. — случайная величина, имеющая распределение
— случайная величина, имеющая распределение .
. ,
, — полная группа событий, и
— полная группа событий, и  — некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что имело место событие
— некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что имело место событие 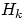 , если в результате эксперимента наблюдалось событие
, если в результате эксперимента наблюдалось событие 

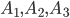 — события выбора счета у первой, второй и третьей организаций. Соответствующие вероятности будут
— события выбора счета у первой, второй и третьей организаций. Соответствующие вероятности будут ,
,  ,
, 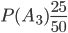
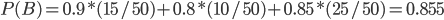
 .
.



