
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Какие события называются случайными?Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте РАЗДЕЛ 1 - Основные понятия Какова природа случайности? A)Случайность свойственна природе изначально Какие события называются случайными? C)Случайное события в результате опыта может произойти или не произойти К каким явлениям целесообразно применять теорию вероятностей? A)К массовым явлениям Какая вероятность измеряет степень уверенности? A)Субъективная вероятность 5.Какое утверждение ошибочно? Основоположниками русской школы теории вероятностей являются: A)Ляпунов А.М. и Буняковский В.Я. B)Хинчин А.Я. и Колмогоров А.Н. Кто из русских и советских ученых разработал аксиоматику современной теории вероятностей? A)Колмогоров А.Н. Чем занимается теория вероятностей? B)Она позволяет определить вероятности сложных событий через вероятности простых событий Чем занимается математическая статистика? A)Она позволяет определять вероятности событий из опыта Какие ученые внесли значительный вклад в развитие математической статистики? Укажите ошибочное утверждение. B)П.Л.Чебышев, А.А.Марков, А.М.Ляпунов Какие теории существенно используют математический аппарат теории вероятностей? Укажите ошибочное утверждение. C)Теория множеств 11.Основоположниками русской школы теории вероятностей являются: A)Ляпунов А.М. и Буняковский В.Я. C)Чебышев П.Л.. и Марков А.А. Какие ученые внесли значительный вклад в развитие математической статистики? A)Е.Е.Слуцкий, А.Н.Колмогоров, В.И.Романовский, Н.В.Смирнов C)К.Пирсон, Р.Фишер, Ю.Нейман, А.Вальд Какие теории существенно используют математический аппарат теории вероятностей? A)Теория надежности, тория массового обслуживания B)Теория информации, теория игр D)Математическая статистика, теория случайных процессов Какое определение вероятности события более верно? C)Вероятность - это число, позволяющее сравнивать степени возможности различных событий В каких пределах может изменяться вероятность события? B)От 0 до 1 Чему равна вероятность достоверного события? B)1 Чему равна вероятность невозможного события? A)0 РАЗДЕЛ 2 - События и множества Какие вы знаете операции над событиями как множествами элементарных событий? Укажите ошибочное утверждение. D)Прореживание Какое соответствие имеется между операциями над событиями и операциями над множествами? Укажите ошибочное утверждение. B)Отрицанию соответствует разность множеств 3.Как обозначается принадлежность элементарного события a множеству A? A) Как обозначается тот факт, что все элементы множества A принадлежат множеству B? A) Множество C получено объединением подмножеств A и B. Какое выражение ошибочно? A) Множество C получено пересечением подмножеств A и B. Какое выражение ошибочно? C) Множество С содержит элементы подмножества В не принадлежащие подмножеству A. Как это записать? A) 8.При обработке партии из 5 деталей возможны события A) 9.При обработке партии из 5 деталей возможны события B) 10.На станке обрабатываются последовательно 3 детали. B) 11.На станке обрабатываются последовательно 3 детали. A) Какие вы знаете операции над событиями как множествами элементарных событий? A)Пересечение (умножение) B)Вычитание C)Объединение (сложение) D)Отрицание Какие соответствия имеются между операциями над событиями и операциями над множествами? A)Произведению событий соответствует пересечение множеств C)Сложению событий соответствует объединение множеств Множество C получено объединением подмножеств A и B. Какие выражения верны? B) РАЗДЕЛ 4 - Комбинаторика 1.Чему равно число перестановок m различных предметов? A) 2.Чему равно число размещений m различных предметов по n, которые отличаются порядком или составом? A) 3.Сколько вариантов будут иметь выборки двух деталей из партии 10 деталей с учетом порядка их обработки? B)90 4.Чему равно число сочетаний из m предметов по n? C) 5.Сколько вариантов будут иметь выборки двух деталей из партии 10 деталей без учета порядка их обработки? A)45 6.Объект a может быть выбран из совокупности объектов m способами. Объект b может быть выбран из той же совокупности n способами. Сколькими способами можно выбрать либо a либо b? B) 7.Объект a может быть выбран из совокупности объектов m способами. Объект b может быть выбран из той же совокупности n способами. Объект c может быть выбран из той же совокупности k способами. Сколькими способами можно выбрать либо a либо b либо с? B) 8.Объект a может быть выбран из совокупности объектов m способами. Объект b может быть выбран из другой совокупности n способами. Сколькими способами можно выбрать пару (a, b)? A) 9.Объект a может быть выбран из первой совокупности объектов m способами. Объект b может быть выбран из второй совокупности n способами. Объект с может быть выбран из третьей совокупности k способами. Сколькими способами можно выбрать тройку (a, b, c)? A) Какое выражение ошибочно? B)0!=0 17. Г(n) – гамма-функция. Какие выражения верны? A) 18.Какое выражение для вычисления факториала называется формулой Стирлинга, если Г(n) – гамма-функция? B) РАЗДЕЛ 5 1.События А и В несовместимы. Чему равна вероятность реализации одного из них [события С ], если известны A) 2.События А и В несовместимы. Чему равна вероятность события E совместной их реализации, если известны B) 3.События А и В совместимы. Известны вероятности A) 4.События А и В совместимы. Чему равна вероятность реализации и А и В [события С ]? C) D) 5.События А и B) 6.События А и A) РАЗДЕЛ 6 Имеется три одинаковые урны. В первой урне 2 белых и 1 черный шар, во 2-ой урне – 3 белых и 1 черный шар, в 3-ей урне – 2 белых и 2 черных шара. Выбираем случайно одну урну и вытаскиваем из нее шар. Какова вероятность, что он белый? B) 9.Имеются две несовместимых гипотезы H1. H2. образующие полную группу. Их вероятности C) 10.В партии 40% деталей обработано на первом станке, а 60% - на втором станке. Вероятность брака на станках P1 и P2 соответственно. Какова вероятность того, что случайно выбранная деталь, оказавшаяся дефективной, обработана на первом станке? A) 11.В партии 40% деталей обработано на первом станке, а 60% - на втором станке. Вероятность брака на станках P1 и P2 соответственно. Какова вероятность того, что случайно выбранная деталь, оказавшаяся дефективной, обработана на втором станке? C) Имеется три одинаковые урны. В первой урне 2 белых и 1 черный шар, во 2-ой урне – 3 белых и 1 черный шар, в 3-ей урне – 2 белых и 2 черных шара. Выбираем случайно одну урну и вытаскиваем из нее шар. Какова вероятность, что он черный? B) РАЗДЕЛ 9 1.Как изменяется функция распределения F(x) неслучайной величины X=a? C)Она при x<a и x>a равна 0, а при x=0 равна 2.Как изменяется плотность распределения f(x) неслучайной величины X=a? Укажите ошибочное утверждение: A)Она при x<a равна 0, а при x 3.Дискретная случайная величина X принимает значения С) 4.Дискретная случайная величина X принимает значения B) 5.Непрерывная случайная величина X имеет функция распределения F(x) и плотность распределения f (x). Чему равно математическое ожидание? A) 6.Непрерывная случайная величина X имеет функция распределения F(x) и плотность распределения f (x). Чему равна дисперсия X? Укажите ошибочное утверждение: B) 7.Как определяется начальные моменты случайной величины X с плотностью f (x) и функцией распределения F(x)? A) 8.Как определяется центральные моменты случайной величины X с плотностью f (x), функцией распределения F(x) и математическим ожиданием C) 9.Что такое мода случайной величины X с плотностью f (x), функцией распределения F(x)? B)Это такое значение x, при котором плотность f (x) максимальна D)Это корень уравнения 10.Что такое медиана случайной величины X с плотностью f (x), функцией распределения F(x)? D)Это такое значение 11.Как изменяется плотность распределения f(x) неслучайной величины X=a? B)Плотность изменяется, как дельта функция C)Она всегда равна 0 кроме точки x=a, где она бесконечна 12.Дискретная случайная величина X принимает значения A) 13.Непрерывная случайная величина X имеет функция распределения F(x) и плотность распределения f (x). Чему равна дисперсия X? A) 14.Что такое медиана случайной величины X с плотностью f (x), функцией распределения F(x)? C)Это решение уравнения D)Это такое значение X= 15.Как определяется третий центральный момент случайной величины X c плотностью распределения f(x)? B) Что верно? B)Математическое ожидание – это первый начальный момент случайной величины Что верно? A)Дисперсия – это второй центральный момент случайной величины РАЗДЕЛ 10 1.Что такое квантиль порядка D) РАЗДЕЛ 11 1.Случайная величина X равномерно распределена в интервале [a, b]. Чему равна ее плотность f (x)? A) 2.Чему равна функция распределения F(x) равномерно распределенной в интервале [a, b] случайной величины X?
B) 3.Чему равно математическое ожидание равномерно распределенной в интервале [a, b] случайной величины X? A) 4.Случайная величина X равномерно распределена в интервале [a, b]. Укажите ошибочное утверждение: B)Дисперсия 5.Случайная величина X равномерно распределена в интервале [a, b]. Чему равна вероятность C)0,5 6.Распределение Симпсона имеет вид равнобедренного треугольника с основанием b-a. Укажите ошибочное утверждение: B)Медиана 7.Распределение Симпсона случайной величины X имеет вид равнобедренного треугольника с основанием b-a. Чему равна плотность при x равном моде? A) 8.Распределение Симпсона случайной величины X имеет вид равнобедренного треугольника с основанием b-a. Укажите ошибочное утверждение. B)Медиана равна 9.Распределение Симпсона имеет вид равнобедренного треугольника с основанием b-a. Чему равна плотность при X равном моде? Укажите ошибочные утверждения. B) 10.Распределение Симпсона случайной величины X имеет вид равнобедренного треугольника с основанием b-a. Укажите ошибочное утверждение. D) 11.Случайная величина X равномерно распределена в интервале [a, b]. Укажите верные утверждения: A)Квадратичное отклонение C)Асимметрия D)Математическое ожидание равно 12.Случайная величина X равномерно распределена в интервале [a, b]. Чему равна вероятность C)0,5 13.Распределение Симпсона имеет вид равнобедренного треугольника с основанием b-a. Укажите верные утверждения. A)Математическое ожидание C)Мода 14.Распределение Симпсона случайной величины X имеет вид равнобедренного треугольника с основанием b-a. Укажите верные утверждения. A) B)Ассиметрия C)Математическое ожидание 15.Случайная величина X равномерно распределена в интервале от a до b. Чему равна мода? A)Мода не имеет определенного значения 16.Случайная величина X равномерно распределена в интервале от a до b. Чему равна функция распределения F(x) при x>b? B)1,0 17.Случайная величина X равномерно распределена в интервале от a до b. Чему равна функция распределения F(x) при x<a? C)0 Какое утверждение ошибочно? A)Произведение нормально распределенных величин имеет нормальное распределение РАЗДЕЛ 16 - Корреляция 1.Как выражается коэффициент корреляции через корреляционный момент и безусловные квадратичные отклонения A) 2.В каких пределах может изменяться коэффициент корреляции rxy? B) 3.Что значит, если rxy = 1? B)X и Y связаны линейно, то есть 4.Если коэффициент корреляции между X и Y rxy = 0, значит ли это, что X и Y независимы? C)не обязательно 5.Для независимости X и Y достаточно ли или необходимо, чтобы коэффициент корреляции rxy = 0? B)необходимо, но не достаточно РАЗДЕЛ 20 1.По какой формуле определяется статистическое среднее, если C) 2.По какой формуле определяется статистическая дисперсия, если A) РАЗДЕЛ 21 РАЗДЕЛ 22 Какие утверждения верны. B)Случайная функция – это случайная величина, зависящая от неслучайного аргумента Что верно? A)Случайный процесс – это случайная функция, неслучайным аргументом которой является время B)Случайный процесс – это случайная величина, зависящая от времени Какие утверждения верны? A)Процесс восстановления – это полумарковский процесс с одним состоянием; B)Альтернирующий процесс – это полумарковский процесс с двумя состояниями; C)Марковский процесс – это полумарковский процесс, у которого времена пребывания имеют показательное распределение; D)Марковский процесс – это процесс все состояния которого обладают марковским свойством;
РАЗДЕЛ 1 - Основные понятия. 1 РАЗДЕЛ 2 - События и множества. 1 РАЗДЕЛ 3 - Определение вероятности. 3 РАЗДЕЛ 4 - Комбинаторика. 4 РАЗДЕЛ 5. 5 РАЗДЕЛ 6. 6 РАЗДЕЛ 7 - Случайные величины и их законы распределения. 7 РАЗДЕЛ 8 - Плотность распределения. 8 РАЗДЕЛ 9. 10 РАЗДЕЛ 10. 11 РАЗДЕЛ 11. 12 РАЗДЕЛ 12 - Дискретные распределения. 14 РАЗДЕЛ 13 - Нормальное и др. распределения. 15 РАЗДЕЛ 14 - Система случайных величин. 16 РАЗДЕЛ 15 – Зависимые и независимые случайные величины.. 18 РАЗДЕЛ 16 - Корреляция. 20 РАЗДЕЛ 17 - Числовые характеристики функций от случайных величин 21 РАЗДЕЛ 18 - Распределение функций случайных аргументов. 22 РАЗДЕЛ 19 - Предельные теоремы.. 23 РАЗДЕЛ 20. 25 РАЗДЕЛ 21. 26 РАЗДЕЛ 22. 28 Раздет 23 - Случайные процессы.. 29
РАЗДЕЛ 1 - Основные понятия Какова природа случайности? A)Случайность свойственна природе изначально Какие события называются случайными? C)Случайное события в результате опыта может произойти или не произойти
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 622; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |


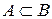


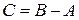
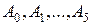 по числу дефектных деталей. Как выражается событие С, состоящее в том, что дефектными являются не более двух деталей?
по числу дефектных деталей. Как выражается событие С, состоящее в том, что дефектными являются не более двух деталей?

 - события, состоящие в том, что дефектными оказываются первая, вторая, третья детали соответственно. Записать событие, состоящее в том, что одна из трех деталей дефектная.
- события, состоящие в том, что дефектными оказываются первая, вторая, третья детали соответственно. Записать событие, состоящее в том, что одна из трех деталей дефектная.








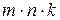
 ; B)
; B)  ; D)
; D) 
 и
и  ?
?
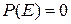
 . Чему равна вероятность события С, состоящего в реализации A или В или А и В?
. Чему равна вероятность события С, состоящего в реализации A или В или А и В? ;
; ;
;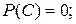
 противоположны. Чему равна вероятность их суммы?
противоположны. Чему равна вероятность их суммы?
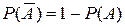 ; B)
; B) 

 и
и  . Известны условные вероятности
. Известны условные вероятности  и
и 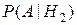 . Какова вероятность
. Какова вероятность  ?
?




 a равна 1
a равна 1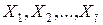 с вероятностями P1, P2, …, Pn. Чему равно математическое ожидание?
с вероятностями P1, P2, …, Pn. Чему равно математическое ожидание?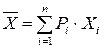




 ;
;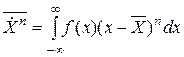

 , что
, что 
 ;
; 
 ; C)
; C) 
 ; C)
; C) 

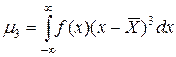
 случайной величины X с плотностью f (x), функцией распределения F(x)? Укажите ошибочное утверждение.
случайной величины X с плотностью f (x), функцией распределения F(x)? Укажите ошибочное утверждение.

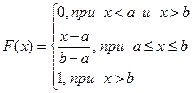
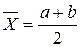
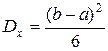
 ?
?
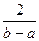

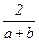 ; C)
; C) 
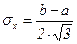
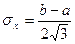

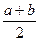
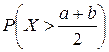 ?
?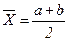
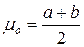

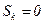


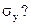


 и
и 
 - реализации случайной величины T?
- реализации случайной величины T?
 ; C)
; C) 



