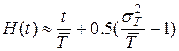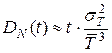Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Как получить уравнения для оценки параметров распределения методом квантилей?Содержание книги
Поиск на нашем сайте
B)Путем приравнивания статистических и теоретических квантилей по числу параметров распределения РАЗДЕЛ 22 Что такое ошибка I-го рода при проверке статистических гипотез? C)Это вероятность отвергнуть гипотезу, если она верна Что такое ошибка II-го рода при проверке статистических гипотез? A)Это вероятность принять гипотезу, если она ошибочна Что такое уровень значимости при проверке статистических гипотез? C)Это вероятность того что критерий согласия превысит допустимые границы, если гипотеза верна (вероятность отклонения правильной гипотезы) Что такое критерий согласия при проверке статистических гипотез? A)Это мера отклонения опытного значения от предполагаемого по гипотезе 5. B) 6.Какому закону распределения подчиняется критерий B)Гамма 7.Что такое “число степеней свободы” в критерии согласия Пирсона, если N – размер выборки, п - число интервалов группирования, k – число оцененных параметров предполагаемого распределения? C)Число степеней свободы равно n-k- 1 8.Как формулируется критерий согласия Колмогорова, если A) 9.Для случайной величины X c предполагаемой плотностью распределения A) n -3 10.Критерий C)Это число степеней свободы Раздет 23 - Случайные процессы Какие утверждения верны. B)Случайная функция – это случайная величина, зависящая от неслучайного аргумента Что верно? A)Случайный процесс – это случайная функция, неслучайным аргументом которой является время B)Случайный процесс – это случайная величина, зависящая от времени Какие случайные процессы бывают? A)Случайные процессы с непрерывным вмешательством случая B)Случайные процессы с дискретным вмешательством случая Какие процессы относятся к классу процессов с непрерывным вмешательством случая? A)Броуновское движение C)Диффузия E)Ветровая нагрузка Какие процессы относятся к классу процессов с дискретным вмешательством случая? B)Процессы массового обслуживания, связанные образование очереди D)Процессы, связанные с отказами структурных единиц машин Что такое процесс восстановления? A)Это последовательность независимых случайных величин с одинаковым распределением, понимаемых как наработки до отказа некоторого объекта, отказы которого мгновенно устраняются C)Это последовательность событий таких, что интервал времени между соседними событиями является независимой случайной величиной с одинаковым распределением Какой процесс восстановления называется простым? B)Если начало отсчета времени совпадает с началом нового цикла процесса Какой процесс восстановления называется стационарным? A)Если начало отсчета времени не связано с моментом восстановления Какой процесс восстановления называется общим? C)Если первое восстановление запаздывает относительно начала отсчета времени на величину (возможно случайную с заданным законом распределения) 10.Чему равно среднее число восстановлений простого процесса восстановления за время t,если B) 11.Чему равна дисперсия числа восстановлений простого процесса восстановления за время t,если B) Какой процесс называется пуассоновским? B)Это такой процесс восстановления, у которого длительность цикла T имеет показательное распределение
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 284; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.117.240 (0.009 с.) |

 - теоретические вероятности а
- теоретические вероятности а  -статистические вероятности попадания случайной величины X в соответствующие интервалы. Какая формула верна для критерия согласия Пирсона, если n – число интервалов, а N – размер выборки?
-статистические вероятности попадания случайной величины X в соответствующие интервалы. Какая формула верна для критерия согласия Пирсона, если n – число интервалов, а N – размер выборки?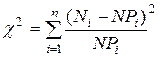 ; C)
; C) 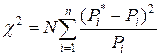
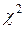 Пирсона?
Пирсона? - предполагаемая теоретическая и статистическая функции распределения случайной величины X?
- предполагаемая теоретическая и статистическая функции распределения случайной величины X?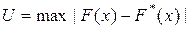
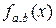 по выборке N реализаций построена гистограмма с n интервалами. Каким следует брать число степеней свободы при обращении к таблице распределения
по выборке N реализаций построена гистограмма с n интервалами. Каким следует брать число степеней свободы при обращении к таблице распределения 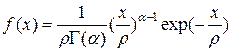 , где
, где 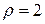 а
а 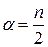 . Что означает параметр n?
. Что означает параметр n?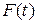 - функция распределения длительности цикла T,
- функция распределения длительности цикла T,  - математическое ожидание,
- математическое ожидание, 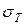 - квадратичное отклонение?
- квадратичное отклонение?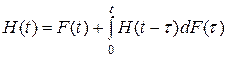 ; C)
; C)