
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Что определяет функция распределения F(x) случайной величины X?Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
C)Вероятность того, что X < x; 4.Чему равна функция распределения F(x) при x = C) F( 5.Чему равна функция распределения при x = - A) F(- 6.Чему равна вероятность того, что X > x? B)1– F(x) 7.Чему равна вероятность того, что X > x1 и X < x2, если x2 > x1? B) F(x2) – F(x1) 8.Чему равна вероятность X = a, если X – непрерывная случайная величина с распределением F(x) и плотностью f(x), a- конкретное значение? B) P(X=a) = 0 9.Как изменяется функция распределения F(x) непрерывной случайной величины X с ростом x? B)Монотонно возрастает от 0 до 1 10.Как изменяется функция распределения F(x) непрерывной случайной величины X с ростом x? A)Монотонно увеличивается от 0 до 1 Как изображается распределение дискретной случайной величины? Укажите ошибочное утверждение. C)В виде графика монотонной возрастающей функции Как изображается распределение дискретной случайной величины? Укажите верные утверждения. A)В виде полигона B)В виде решетчатой диаграммы D)В виде ряда значений и соответствующих им вероятностям Какая случайная величина называется дискретной? Укажите верные утверждения. A)Если она занимает только целочисленные значения C)Если возможные значения можно пронумеровать 14.Как изменяется функция распределения F(x) дискретной случайной величины X с ростом x? A)Ступенчато увеличивается от 0 до 1 15.Чему равна вероятность того, что X >m для дискретной случайной величины, заданной вероятностями B)
16.Чему равна вероятность того, что X<m для дискретной случайной величины, заданной вероятностями A) РАЗДЕЛ 8 - Плотность распределения 1.Как определяется плотность распределения непрерывной случайной величины X через функцию распределения F(x)? B) Может ли плотность случайной величины принимать отрицательные значения? B)Не может 3.Как выражается функция распределения F(x) через плотность распределения f (x)? C) 4.Чему равна вероятность, что случайная величина X больше a и меньше b, b > a? A) P(a<X<b) = 5.Какова вероятность того, что случайная величина с плотностью распределения f (x) попадет в интервал x, x+dx, где A) 6.Чему равен интеграл B)1 7.Чему равна вероятность того, что Х>a, если f(x) – плотность распределения Х?
B) 8.Чему равна вероятность того, что Х>a, если F(x) – функция распределения Х? A) 9.Чему равна вероятность, что случайная величина X больше a и меньше b, b > a, если F(x) – функция распределения Х? B) P(a<X<b) =F(b)-F(a) 10.Непрерывно распределенная величина Х имеет плотность f(x). Чему равна вероятность P(X=a), где а фиксированное число? A) 11.Как определяется плотность распределения непрерывной случайной величины X через функцию распределения F(x)? B) 12.Чему равна вероятность того, что Х>a, если f(x) – плотность распределения Х, a F(x)- функция распределения? B) Может ли плотность случайной величины принимать значения большие 1? B)Может 14.Может ли функция распределения F(x) случайной величины X принимать отрицательные значения? A)Не может 15.Может ли функция распределения F(x) случайной величины X принимать значения большие 1? A)Не может 16.Непрерывно распределенная величина Х имеет плотность f(x) и функцию распределения F(x). Чему равна вероятность P(X=a), где а фиксированное число? A) 17.Непрерывно распределенная величина Х имеет плотность f(x) и функцию распределения F(x). Какие утверждения ошибочны, если а фиксированное число? B) РАЗДЕЛ 9 1.Как изменяется функция распределения F(x) неслучайной величины X=a? C)Она при x<a и x>a равна 0, а при x=0 равна 2.Как изменяется плотность распределения f(x) неслучайной величины X=a? Укажите ошибочное утверждение: A)Она при x<a равна 0, а при x 3.Дискретная случайная величина X принимает значения С) 4.Дискретная случайная величина X принимает значения B) 5.Непрерывная случайная величина X имеет функция распределения F(x) и плотность распределения f (x). Чему равно математическое ожидание? A) 6.Непрерывная случайная величина X имеет функция распределения F(x) и плотность распределения f (x). Чему равна дисперсия X? Укажите ошибочное утверждение: B) 7.Как определяется начальные моменты случайной величины X с плотностью f (x) и функцией распределения F(x)? A) 8.Как определяется центральные моменты случайной величины X с плотностью f (x), функцией распределения F(x) и математическим ожиданием
C) 9.Что такое мода случайной величины X с плотностью f (x), функцией распределения F(x)? B)Это такое значение x, при котором плотность f (x) максимальна D)Это корень уравнения 10.Что такое медиана случайной величины X с плотностью f (x), функцией распределения F(x)? D)Это такое значение 11.Как изменяется плотность распределения f(x) неслучайной величины X=a? B)Плотность изменяется, как дельта функция C)Она всегда равна 0 кроме точки x=a, где она бесконечна 12.Дискретная случайная величина X принимает значения A) 13.Непрерывная случайная величина X имеет функция распределения F(x) и плотность распределения f (x). Чему равна дисперсия X? A) 14.Что такое медиана случайной величины X с плотностью f (x), функцией распределения F(x)? C)Это решение уравнения D)Это такое значение X= 15.Как определяется третий центральный момент случайной величины X c плотностью распределения f(x)? B) Что верно? B)Математическое ожидание – это первый начальный момент случайной величины Что верно? A)Дисперсия – это второй центральный момент случайной величины РАЗДЕЛ 10 1.Что такое квантиль порядка D)
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 842; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.218.124 (0.007 с.) |

 ?
? ?
? ?
?




 ?
?
 , где f (x) – плотность распределения случайной величины X?
, где f (x) – плотность распределения случайной величины X?


 ; C)
; C) 
 a равна 1
a равна 1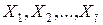 с вероятностями P1, P2, …, Pn. Чему равно математическое ожидание?
с вероятностями P1, P2, …, Pn. Чему равно математическое ожидание?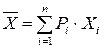




 ;
;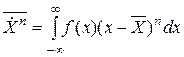

 , что
, что 
 ;
; 
 ; C)
; C) 
 ; C)
; C) 

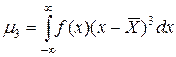
 случайной величины X с плотностью f (x), функцией распределения F(x)? Укажите ошибочное утверждение.
случайной величины X с плотностью f (x), функцией распределения F(x)? Укажите ошибочное утверждение.



