
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 10. Основные законы распределения НСВ.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Опр1. Говорят, что НСВ Химеет равномерный закон распределения на отр. [ a; b], если ее плотность вер-ти имеет вид f(x)= {1/(b-a), a<=x<=b}{ 0, x<a или x> b} Теорема 1. Фнкция распределения НСВ Х, распределенная по равномерному закону имеет вид F(x)={0, x<=a}{x-a/b-a, a<x<=b}{1, x>b}. Док-во. Функция распределения F(x) = [cв-во 4 пл-ти вер-ти]=-∞ ∫x f(t)dt. 1. x<=a,=> F(x) = -∞ ∫xf(t) dt=-∞ ∫x0dt=0. 2.a<x<=b, => F(x) = -∞ ∫xf(t) dt=[-∞ ∫х=-∞ ∫a+ a ∫x]= a∫xf(t)dt= a ∫x (1/b-a)dt=(1/b-a)a ∫xdt=(1/b-a)t│ab=x-a/b-a. 3. x>b, => F(x) = -∞ ∫xf(t) dt=[-∞ ∫x= -∞∫a+ a ∫b+ b ∫x]= a ∫bf(t)dt= a ∫b (1/b-a)dt =1/b-a a ∫bdt =(1/b-a)t│a b=b-a/b-a=1. Теорема 2. МО и дисперсия CВ Х, распределенной по равномерному закону соответственно равны М(Х)= (а+b)/2; D(X)=(b-a)2/12. Док-во: M(X)=def-∞∫∞xf(x)dx=!-∞∫∞=-∞∫a(=0)+a∫b+b∫∞(=0)!= a∫bxdx/b-a=1/b-a a∫bxdx=1/b-a(x2/2)!ba=b2-a2/2(a-b)=a+b/2 D(X)=def-∞∫∞(x-M(x))^2f(x)dx=!-∞∫∞=-∞∫a(=0)+a∫b+b∫∞(=0)!=a∫b ((x-(b+a)/2)^2)dx/b-a=1/b-aa∫b((x-(b+a)/2)^2)dx= (b-a)^2/12 Замечание! Равномерное распределение не имеет моды, а медиана совпадает с МО, т.е. Ме(Х) =(a+b)/2 (ошибки измерения физ велечин при окр рез набл до ближайшего деления) Опред №2 Говорят, что НСВ Х имеет показательный (экспоненциальный) закон расп-ния с параметром λ, если ее плотность вер-ти имеет вид f(x)={ λ*e^-λx, x>=0} { 0, x<0}. Теорема 3. Функция расп-ния CВ Х, распределенной по показ. закону, имеет вид F(X)={ 1-e^-λx, x>=0} { 0, x<0 }. Док-во: -∞∫xf(t)dt Пусть x<0 =>-∞∫xf(t)dt=-∞∫x0dt=0. Пусть x≥0 =>-∞∫xf(t)dt=!-∞∫x=-∞∫0(=0)+0∫x!= 0∫xf(t)dt=0∫xλe-λxdt=λ0∫x e-λxdt=λ(e-λx/-λ)!x0=-(e-λt)!x0=-(e-λx-1)=(-e)-λx-1
Теорема 4. МО и дисперсия CВ Х,распределенной по показ. закону, соответственно равны М(Х)=1/λ; D(X)= 1/ λ2. Док-во: Проверим для МО. M(X)=def-∞∫∞xf(x)dx=!-∞∫∞=-∞∫0(=0)+0∫∞!=0∫∞xλ e-λxdx=def lim b→∞ 0∫bλxe-λxdx. 0∫bλxe-λxdx=!интегр по частям!=!u=λx,dv=e-λxdx, v=∫e-λxdx=e-λx/-λ, du=λdx!=[λx*e-λx/-λ]!b0-0∫be-λx λdx /-λ=-[x e-λx]!b0+0∫be-λxdx=-[be-λb-0]+(e-λx/-λ)!b0= -be-λb-1/λ (e-λb-1)= -be-λb-e-λb/λ+1/2 =>M(X)=lim b→∞[-be-λb-e-λb/λ+1/2]=1/λ Опр3 (норм закон распределения). Говорят, чтоНСВ Х имеет нормальный закон расп-ния (закон Гаусса) с параметрами δ и μ, если ее плотность вероятности имеет вид f(x) = (1/√2π* δ)* e^-(x-μ)^2/2δ^2, (δ>0)/
Замечание. Функция распр-ния CВ Х, распред-ная по норм. закону имеет вид F(X)=(1/√2π* δ)--∞∫xe^-(t-μ)^2/2δ^2dt. Теорема 5. МО, дисперсия и СКО СВ Х, распр-ной по норм. закону соответственно равны М(Х)=μ, D(X)= δ2, δ(X)= δ Замечаение! Утверждение «CВ Х имеет норм. распределение с параметрами μ и δ» кратко записывается Х? N (μ, δ) Опр4. Норм.закон распределения CВ Х с парметрами μ=0, δ=1,т.е. N(0;1) назыв. стандартным или нормированным. Замечание! Плотность вер-ти и ФР СВ Х, распределенной по нормированному закону, имеют вид f0(x)=(1/√2π)e^-x^2/2 ; F(X) =-∞∫x (1/√2π) е^-t^2/2dt. Эти функции табулированы (сущ-ют таблицы их значений). Свойства CВ Х распред-ной по нормированному закону (X? N(μ;δ)) 1.Вер-ть попадание CВ Х в отрез. [ a;b] P{a<=x<=b}=F0(b-μ/δ)- F0(а-μ/δ) 2. вер-ть того, что CВ Х отличается от своего МО по абс. вел-не не больше, чем на ε P{X-μ<=ε}=2F0(ε/δ)-1.
Лекция 11.О1. Упорядоченный набор (x1, x2,.., xn) СВ Х1, Х2, …, Хn называется системой n случайных величин или многомерной (nмерной) случайной величиной. О2. Одномерные СВ Х1, Х2, …,Хn называются компонентами или составляющими n- мерной СВ (Х1, Х2, …, Хn) Зам! Свойство систем Св многомерной Св не исчерпывается свойствами её компонентов, а включает также и взаимные связи (зависимости между этими компонентами). В дальнейшем будем рассматривать только 2 мерную СВ. Типы 2 мерных Случайных Величин (X,Y) Дискретная – если возможные значения (X,Y) образуют конечное или счётное множество. Непрерывная – если возможные значения (X,Y) сплошь заполняют некоторую область на плоскости. Смешанная - если возможные компоненты X и Y являются одномерными СВ разных типов. З! Тип 2 мерной СВ (X,Y) фактически определяется типом её компонентов X иY т.е. если оба компонента x и y ДСВ, то и 2 мерная СВ (X,Y) также будет дискретной. О3 Матрицей распределения называется матрица вида:
Свойства Вероятности
Зам! Свойства 2 и 3 означают, что если задана матрица распределения 2мерной ДСВ (X,Y), то можно найти ряды распределения одномерных СВ Х и Y Опр4 Функция распределения 2мерной СВ (X,Y) называется вероятность совместного выполнения 2х неравенств:
Зам! Событие Функция распределения двумерной ДСВ (X,Y) Если СВ (x,y) является дискретной, то её функция распределения находится по формуле
Свойства функции распределения 2 мерной СВХ
Лекция 12 Опр 1. Плотностью вероятности 2мерной НСВ (X,Y) называется вторая смешанная частная производная её функции распределения:
Опр 2. График плотности вероятности 2 мерной НСВ называется поверхностью распределения. Свойства плотности вероятности двумерной НСВ f(x,y)больше или равно 0 Вероятность попадания случайной точки () в область D равна 2му интегралу от плотности вероятности по этой области т.е.
Функция распределения двумерной НСВ может быть выражена через её плотность вероятности по формуле:
Условия нормировки: 2ой несобственный интеграл в бесконечных пределах от плотности вероятности двумерной НСВ равен единице т.е.
Геометрически данное свойство означает, что объем тела, ограниченного сверху поверхностью распределения, а снизу плотностью x по y равна 1
Равномерное распределение 2мерной НСВ Опр3. Говорят, что двумерное НСВ (X,Y) имеет равномерное распределение в области D, если её плотность вероятности имеет вид: f(x,y)= где SD – площадь P замечание: Основные свойства равномерного распределения состоит в том,что для него применимо понятие “Изометрической вероятности” т.е. если область g содержится в области D, то нетрудно показать, что
Теорема (о независимости 2 СВ) СВ независимы
Доказательство: Необходимо: Пусть СВ x и y независимы, тогда
Достаточно: Пусть Тогда из определений функций распределения следует равенство: Следствие:Необходимым и достаточным условием независимости 2ух непрерывных СВ X и Y образующих систему (x,y) является равенство:
Лекция 13 Опр. 1. Условным законом распределения СВ Х входящей в систему (X,Y) называется её закон распределения вычисленный при условии, что другая СВ Y приняла определенное значение. Замечание. Аналогично определяется условный закон распределения СВ Y входящей в систему (X,Y). Обозначим через Замечание! Условные вероятности Опр. 2. Условным законом распределения составляющий x при Замечание. Аналогично находят условный закон распределения составляющий Y Замечание. Сумма вероятностей условного распределения равна 1. Док-во:
Аналогично доказывается, что при фиксированным Опр.3. Условной плотностью вероятности
Лекция 14 Опр. 1. МО двумерной ДСВ (X,Y) называется совокупность двух МО M(X) и M(Y) определяемых равенствами Опр. 2. МО двумерной НСВ с плотностью вероятности f(x,y) называется совокупность двух МО M(x) и M(y) определяемые равенствами Опр. 4. Дисперсией двумерной НСВ (X,Y) с плотностью вероятности f(x,y) называется совокупность двух дисперсий D(x) и D(y) определяемых равенствами Опр.5.Ковариацией СВ X и Y называется МО произведения отклонений этих величин. Обозначается cov (X,Y) или Замечание! Ковариацию часто удобно вычислять по формуле, которая получается из определения ковариации на основании свойств МО СВ X и Y называется выражение
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 977; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.103.8 (0.012 с.) |



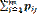 =
= 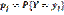
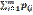 =
= 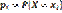
 т.е. F(x,y)=P
т.е. F(x,y)=P 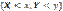
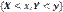 означает произведение событий
означает произведение событий 
 ; где суммируются все вероятности
; где суммируются все вероятности 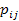 для которых
для которых 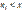 ,
, 
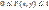
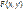 – не убывающая функция по каждому аргументу т.е.
– не убывающая функция по каждому аргументу т.е. 

 , if
, if 


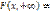 Fx(x)
Fx(x)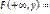 Fy(y) где Fx(x) и Fy(y)функции распределения СВ Х и Y соответственно.
Fy(y) где Fx(x) и Fy(y)функции распределения СВ Х и Y соответственно.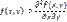


 =1
=1 )=
)=  )=
)= 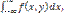 где
где  и
и  ) плотность вероятности СВ(X,Y) соответственно.
) плотность вероятности СВ(X,Y) соответственно.
 где
где  площадь g
площадь g функция распределения двумерной СВ (X,Y) равна произведению функций распределения составляющих т.е.
функция распределения двумерной СВ (X,Y) равна произведению функций распределения составляющих т.е.
 )= F(x,y),
)= F(x,y), 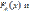
 ) функции распределения СВ x и y соответственно.
) функции распределения СВ x и y соответственно.
 )
)
 )
) , которое и означает, что СВ X и Y независимы ч.т.д.
, которое и означает, что СВ X и Y независимы ч.т.д.
 )= F(x,y)
)= F(x,y) условную вероятность, того что СВ Х примет значение
условную вероятность, того что СВ Х примет значение  при условии, что СВ Y приняла значение
при условии, что СВ Y приняла значение 
 определяются равенством:
определяются равенством: 
 называют совокупность условных вероятностей
называют совокупность условных вероятностей 
 Вычисленных предположений, что событие уже наступило.
Вычисленных предположений, что событие уже наступило.





 . Это свойство распределений используют для контроля вычислений.
. Это свойство распределений используют для контроля вычислений. составляющей X при заданном значении Y=y называется отношение плотности вероятности двумерной непрерывной СВ (X,Y) к плотности вероятности составляющей Y т.е.
составляющей X при заданном значении Y=y называется отношение плотности вероятности двумерной непрерывной СВ (X,Y) к плотности вероятности составляющей Y т.е.  Аналогично определяется условная плотность вероятности составляющей Y при заданном значении X=x
Аналогично определяется условная плотность вероятности составляющей Y при заданном значении X=x  Формулы для вычисления условных плотностей вероятностей. Если известна плотность вероятности f(x,y) двумерной непрерывной СВ (X,Y), то условные плотности вероятности составляющих X и Y могут быть найдены по формулам
Формулы для вычисления условных плотностей вероятностей. Если известна плотность вероятности f(x,y) двумерной непрерывной СВ (X,Y), то условные плотности вероятности составляющих X и Y могут быть найдены по формулам 
 Замечание! Условные плотности вероятности обладают всеми свойствами безусловной плотности вероятности.
Замечание! Условные плотности вероятности обладают всеми свойствами безусловной плотности вероятности.
 , где
, где 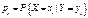 .
.
 . Опр. 3. Дисперсией двумерной ДСВ (x,y) называется совокупность двух дисперсий D(x) и D(y) определяемых равенствами
. Опр. 3. Дисперсией двумерной ДСВ (x,y) называется совокупность двух дисперсий D(x) и D(y) определяемых равенствами 
 .
.
 З! МО M(x),M(y) и дисперсии D(x),D(y) СВ X и Y входящих в систему (X,Y) могут быть найдены по обычным формулам используемых для одномерных СВ. Для этого необходимо предварительно перейти от закона распределения двумерной СВ (X,Y) соответственно к одномерным законам распределения СВ X и Y
З! МО M(x),M(y) и дисперсии D(x),D(y) СВ X и Y входящих в систему (X,Y) могут быть найдены по обычным формулам используемых для одномерных СВ. Для этого необходимо предварительно перейти от закона распределения двумерной СВ (X,Y) соответственно к одномерным законам распределения СВ X и Y
 . Замечание. Ковариация характеризует взаимную зависимость СВ X и Y
. Замечание. Ковариация характеризует взаимную зависимость СВ X и Y  - Для ДСВ
- Для ДСВ  -НСВ
-НСВ . Если СВ независимы то k=0. Опр.6. Коэф. корреляции
. Если СВ независимы то k=0. Опр.6. Коэф. корреляции . Замечание! Для любых СВ X и Y выполняется соотношение
. Замечание! Для любых СВ X и Y выполняется соотношение 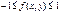 , при этом если r=0, то СВ X и Y называются некореллированы, в противном случае – кореллированы.
, при этом если r=0, то СВ X и Y называются некореллированы, в противном случае – кореллированы.


