Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые законы распределений случайных величинСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
В теории вероятностей и математической статистике выводится большое количество специальных законов распределений СВ, широко используемых в различных отраслях науки и техники. Мы ограничимся рассмотрением лишь тех, которые наиболее часто применяются в эконометрическом анализе. Эти распределения используются для нахождения интервальных оценок, при проверке статистических гипотез, в дисперсионном и регрессионном анализе. Для удобства практического использования распределений СВ разработаны таблицы α-квантилей (критических точек), которые позволяют быстро и эффективно оценивать соответствующие вероятности [16] (см. Приложения). Критической точкой уровня α ( α -квантилем) называется такое значение хα СВ Х, при котором выполняется условие:
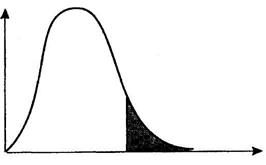
С геометрической точки зрения нахождение квантиля х α заключается в выборе такого значения х, при котором площадь заштрихованной области на рис. 1.4 была бы равна α.
Рис. 1.4.
Для симметричных относительно оси ординат распределений можно ввести понятие двустороннего α-квантиля – Р(| х | > x α). Нахождение α-квантиля (критической точки) определяется величиной (уровнем значимости) самого α и числом степеней свободы рассматриваемых распределений.
Нормальное распределение
Нормальный закон распределения (распределение Гаусса) является предельным случаем почти всех реальных распределений вероятности. Поэтому он используется в очень большом числе практических приложений. Непрерывная СВ Х имеет нормальное распределение, если ее плотность вероятности имеет вид:
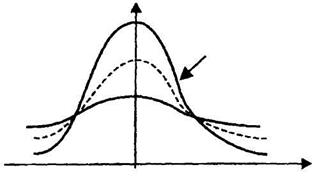
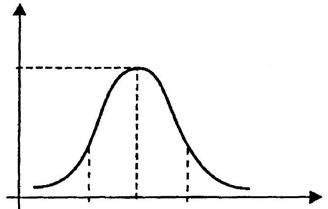
Нормальное распределение (рис. 1.5) полностью определяется двумя параметрами - математическим ожиданием m = M (X) и средним квадратическим отклонением - σ = σ(Х) - и символически обозначается Х ~ N (m, σ2) или X ~ N (m, σ). При изменении числовой характеристики m нормальная кривая перемещается вдоль оси Ох, при изменении σ меняется форма кривой. Нормальный закон распределения с числовыми характеристиками (параметрами) m = 0 и σ2 = 1 называется стандартным распределением.
Рис. 1.5.
Для практических расчетов вероятностей СВ, подчиняющихся нормальному распределению, удобно пользоваться таблицами значений функции Лапласа (Приложение 1). Функция (интеграл вероятностей) Лапласа Ф (u) имеет вид:
где F(u) - функция стандартного нормального распределения СВ U, Р (х 1 £ Х £ х 2) = Ф (u 2) – Ф (u 1), (1.14) где Кроме того, справедливы следующие соотношения: Р (| Х - m | < σ) = 0,68; P(| Х - m | < 2σ) = 0,95; P(| Х - m | < 3σ) = 0,9973, где | Х - m | - отклонение СВ Х от математического ожидания. Другими словами, значения нормально распределенной СВ Х на 95 % сосредоточены в области (m - 2σ, m + 2σ) и на 99,73 % сосредоточены в области (m - 3σ, m + 3σ). Следует также отметить, что линейная комбинация произвольного количества нормальных СВ имеет нормальное распределение. В том случае, когда логарифм СВ подчинен нормальному закону, говорят, что она имеет логарифмически нормальное (логнормальное) распределение.
1.3.2. Распределение χ2 (хи-квадрат)
При моделировании экономических процессов достаточно часто приходится рассматривать СВ, которые представляют собой алгебраическую комбинацию нескольких СВ. Возможность прогнозирования поведения таких СВ осуществляется при использовании ряда специально разработанных законов распределений. К ним относятся χ2-распределение, распределения Стьюдента и Фишера-Снедекора. Пусть имеется n независимых СВ Хi, i = 1, 2 … n, распределенных по нормальному закону, с математическими ожиданиями mi и средними квадратическими отклонениями σ i, соответственно. Если считать, что математическое ожидание каждой из них равно нулю, а среднее квадратическое отклонение – единице, тогда СВ Ui = (Xi - mi)/σ i имеют стандартное нормальное распределение, Ui ~ N (0,1). Распределением χ 2 с ν = n степенями свободы называется распределение суммы квадратов n независимых СВ Ui
Число степеней свободы ν исследуемой СВ определяется числом СВ ее составляющих, уменьшенным на число линейных связей между ними. Например, число степеней свободы СВ, являющейся композицией n случайных величин, которые в свою очередь связаны m линейными уравнениями, определяется как ν = n - m. Распределение χ2 определяется одним параметром - числом степеней свободы ν: М (χ2) = ν = n - m, D (χ2) = 2 ν = 2(n - m). График плотности вероятности СВ, имеющей χ2-распределение, расположен только в первой четверти декартовой системы координат и имеет асимметричный вид с вытянутым правым «хвостом». С увеличением числа степеней свободы распределение χ2 постепенно приближается к нормальному распределению. Таблицы критических точек χ2-распределения приведены в Приложении 3.
Распределение Стьюдента
Рассмотрим стандартную нормальную СВ U ~ N (0,1) и независимую от нее СВ V, распределенную по закону χ2 с ν = n степенями свободы (обозначается V ~
называется распределением Стьюдента (псевдоним английского химика и статистика Госсета) или t -распределением с n -степенями свободы (tn). При n > 2 M (t) = 0 и D (t) = n / n - 2. График функции плотности вероятности СВ, имеющей распределение Стьюдента, является симметричной кривой относительно оси ординат (рис. 1.6) [11].
Рис. 1.6.
С увеличением числа степеней свободы распределение Стьюдента приближается к стандартному нормальному закону и практически при n > 30 можно считать t -распределение приближенно нормальным. Таблица критических точек распределения Стьюдента для различных значений уровня значимости α и числа степеней свободы ν (t α ,ν ) представлена в Приложении 4.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 518; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.009 с.) |

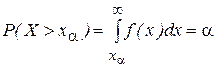 (правосторонний критерий). (1.11)
(правосторонний критерий). (1.11)
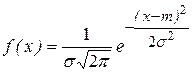 . (1.12)
. (1.12)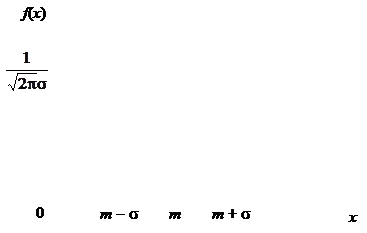
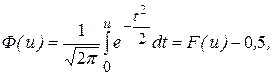 (1.13)
(1.13)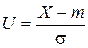 . Тогда вероятность попадания СВ Х, распределенной по нормальному закону, в интервал [ х 1, х 2].
. Тогда вероятность попадания СВ Х, распределенной по нормальному закону, в интервал [ х 1, х 2].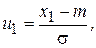
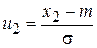 .
.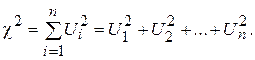 (1.15)
(1.15) ). Тогда распределение случайной величины
). Тогда распределение случайной величины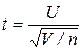 (1.16)
(1.16)