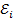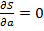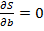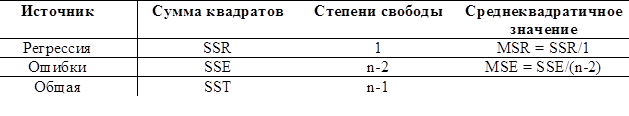Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение Пуассона: формула расчета вероятности, функция распределения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Содержание
1. Испытание Бернулли и биномиальное распределение. Обобщение испытания Бернулли на случай k исходов (k > 2).
Испытание Бернулли – случайный эксперимент, имеющий всего 2 исхода (успех и неудача). Серия испытаний – повторение испытания Бернулли n-раз. Вероятность исходов при этом неизменна.
p (успех) ≥ 0 q (успех) ≥ 0 p + q = 1
Вероятность наступления каждого из исходов определяется по формуле умножения вероятностей. Например, вероятность наступления двух успехов в двух испытаниях: P = pp. Сумма вероятностей для всех исходов будет равен 1.
Биномиальное распределение возникает в случаях, когда нас интересует, сколько раз происходит некоторое событие в серии из определенного испытания.
Биномиальное распределение X = n (целое, 0 ≤ n ≤ k) имеет формулу:
Где k – все испытания, n – число успехов, p – вероятность успеха, q – вероятность неуспеха.
Понятие функции плотности распределения для непрерывных случайных величин.
В случайных экспериментах многие показатели имеют числовое выражение. К примеру, рост, возраст и вес случайно выбранного человека – будет случайной величиной. Главное, что случайная величина всегда зависит от исхода случайного эксперимента.
Существует два вида случайных величин: дискретные (множество значений конечно и счетно) и непрерывные (значения – непрерывное множество).
В отличие от дискретной случайной величины непрерывные случайные величины невозможно задать в виде таблицы ее закона распределения поскольку невозможно перечислить и выписать в определенной последовательностей все ее значения. Одним из возможных способов задания непрерывной случайной величины является использование функции или плотности распределения. Плотностью распределения вероятностей непрерывной случайной величины
Для описания распределения вероятностей дискретной случайной величины плотность распределения неприменима. Зная плотность распределения, можно вычислить вероятность того, что непрерывная случайная величина примет значение, принадлежащее заданному интервалу. Теорема. Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу, равна определенному интегралу от плотности распределения, взятому в пределах от a до b.
Доказательство. Используя соотношение, ( Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале) Область применения. Использование стандартных нормальных величин в проверках гипотез (Уилкоксон)
Статистика Уилкоксона, используемая для проверки гипотезы о равенстве распределений (медиан) двух выборок (W*), если выполняются допущения (выборки независимы между собой, законы распределений непрерывны), и при большом количестве наблюдений в выборках распределена приблизительно по нормальному закону с параметрами (0;1). Для проверки гипотезы наблюдаемое значение сравнивается со стандартной величиной z α\2.
Распределение суммы Сумма двух независимых нормальных величин тоже распределена нормально, причем X1+X2 ~(a1+a2; σ1 2 +σ2 2)
E(X1+X2) = E(X1) + E(X2) = a1+a2 Или E(a1+ σ1 2Z, a2+ σ2 2Z)= E (a1+ σ1 2Z)+E(a2+ σ2 2Z)= a1+a2 D(X1+X2) =D(X1) +D (X2) +2Cov(X,Y)= σ1 2 +σ2 2 (т.к. Cov(X,Y)=0 – так как независимые) Или D(a1+ σ1 2Z, a2+ σ2 2Z)= D (a1+ σ1 2Z)+D(a2+ σ2 2Z) +2Cov(a1+ σ1 2Z, a2+ σ2 2Z) = = σ1 2 +σ2 2 +0= σ1 2 +σ2 2 (* - Доказательство нормальности суммы величин, приведенное в учебнике Макарова «Теория вероятностей» (с.183-184), основано на построении совместной плотности, переходе к полярным координатам и нахождении двойного интеграла. Никогда не разбирали такое – наверное, не понадобится) Биномиальное распределение У этого распределения два параметра: n (количество испытаний) и p (вероятность успеха в одном испытании), =>к=2. 1. Мы знаем, что для биномиального распределения μ1 = Mξ = n×p; В соответствии с Замечанием 2 мы для второго уравнения используем второй центральный момент: α2 = Dξ = n×p×q= n×p×(1–p) 2. Соответствующие эмпирические моменты m1 = 3. Составляем систему уравнений np= Мощность критерия План ответа: 1. Понятие. Связь с ошибкой второго рода. 2. Что значит мощность критерия? Как ее увеличить? Мощность критерия (1-β) – способность текста обнаруживать альтернативную гипотезу или способность отвергнуть нулевую гипотезу, при условии, что верна альтернатива. Иными словами, мощность критерия – вероятность отвергнуть неверную нулевую гипотезу. Мощность критерия непосредственно связана с ошибкой второго рода – вероятностью не отвергнуть неверную нулевую гипотезу. Мощность = 1- β (отвернуть и не отвергнуть гипотезу – противоположные события, поэтому мощность в сумме с ошибкой второго рода дает 1). Таким образом, для расчета мощности необходимо знать распределение статистики по альтернативной гипотезе.
 
Мощность критерия показывает, насколько сильна статистика, насколько тест может обнаруживать ошибки. Чем больше мощность, тем меньше вероятность не отвергнуть неверную гипотезу. Увеличить мощность критерия можно 2 основными способами: 1) Увеличить размер выборки (размер определяет ошибку выборки: с увеличением числа наблюдений уменьшается стандартная ошибка → увеличивается мощность). Проблема: не всегда возможно увеличить выборку (ограниченность ресурсов) 2) Увеличить rejection region – область отвержения гипотезы: Проблема: при таком способе увеличении мощности мы увеличиваем вероятность ошибки первого рода (нельзя одновременно уменьшить обе ошибки). + еще можно уменьшить дисперсию совокупности (примерно тот же эффект, что и от увеличения выборки). Этого можно добиться, например, увеличивая точность измерений. Условия Гаусса-Маркова Для того чтобы полученные по МНК оценки коэффициентов регрессии обладали определенными статистическими свойствами, необходимо выполнение ряда предпосылок оцениваемой модели, называемыми условиями Гаусса-Маркова. N. B.! Рассматриваеттся модель парной регрессии, в которой наблюдения Y связаны с X следующей зависимостью: Yi = β0 + β1xi + Чтобы оценки МНК были эффективны в классе линейных несмещенных оценок (BLUE), необходимо, чтобы данные обладали следующими свойствами: 1. Ошибки не носят систематического характера - Случайный член может быть иногда положительным, иногда отрицательным, но он не должен иметь систематического смещения ни в каком из двух возможных направлений. Если уравнение регрессии включает постоянный член (β0), то это условие чаще всего выполняется автоматически, так как постоянный член отражает любую систематическую, но постоянную составляющую в 2. Дисперсия ошибок одинакова и равна некоторой 3. Отсутствие автокорреляции COV ( 4. Все Но мы можем использовать более слабое условие – X i и 5. * Нормальность ошибок: Пример Допустим у нас есть три точки (1, 3); (2, 5); (3, 6). C помощью этого выведем остатки.
Выведем уравнение для S = (3 – a – b)2 + (5 – a – 2b)2 + (6 – a – 3b)2 = 3a2 + 14b2 + 12ab – 28a – 62b + 70 Теперь нам надо найти такие значения a и b (оценок коэффициентов нашей регрессии), чтобы S была минимальной, для этого мы находим значения a и b, удовлетворяющие следующим условиям:
Получаем систему уравнений: 6a + 12b – 28 = 0 28b + 12a – 62 = 0 Решаем, получаем, что уравнение регрессии будет иметь следующий вид:
Нулевая гипотеза: модель регрессии не объясняет вариацию признака Альтернативная гипотеза: модель регрессии удовлетворительно объясняет вариацию признака
Для проверки модели регрессии с помощью ANOVA необходимо подсчитать объясненную нашей моделью вариацию (ESS) и сумму квадратов остатков (RSS). О том, как это делается – см. билет 23 и 28. Понять, как используется ANOVA в случае линейной регрессии проще всего на примере гипотетической выдачи SPSS:
|
| Вопрос 1 | |
| Вопрос 2 | |
| Вопрос 3 | |
| Вопрос 4 | |
| Вопрос 5 | |
| Вопрос 6 | |
| Вопрос 7 | |
| Вопрос 8 | |
| Вопрос 9 | |
| Вопрос 10 | |
| Вопрос 11 | |
| Вопрос 12 | |
| Вопрос 13 | |
| Вопрос 14 | |
| Вопрос 15 | |
| Вопрос 16 | |
| Вопрос 17 | |
| Вопрос 18 | |
| Вопрос 19 | |
| Вопрос 20 | |
| Вопрос 21 | |
| Вопрос 22 | |
| Вопрос 23 | |
| Вопрос 24 | |
| Вопрос 25 | |
| Вопрос 26 | |
| Вопрос 27 | |
| Вопрос 28 | |
| Вопрос 29 | |
| Вопрос 30 | |
| Вопрос 31 | |
| Вопрос 32 | |
| Вопрос 33 |
1. Испытание Бернулли и биномиальное распределение. Обобщение испытания Бернулли на случай k исходов (k > 2).
Испытание Бернулли – случайный эксперимент, имеющий всего 2 исхода (успех и неудача). Серия испытаний – повторение испытания Бернулли n-раз. Вероятность исходов при этом неизменна.
p (успех) ≥ 0
q (успех) ≥ 0
p + q = 1
Вероятность наступления каждого из исходов определяется по формуле умножения вероятностей. Например, вероятность наступления двух успехов в двух испытаниях: P = pp. Сумма вероятностей для всех исходов будет равен 1.
Биномиальное распределение возникает в случаях, когда нас интересует, сколько раз происходит некоторое событие в серии из определенного испытания.
Биномиальное распределение X = n (целое, 0 ≤ n ≤ k) имеет формулу:
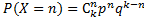
Где k – все испытания, n – число успехов, p – вероятность успеха, q – вероятность неуспеха.
Распределение Пуассона: формула расчета вероятности, функция распределения.
Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
Область значения: Х – любое; 0 ≤ Х ≤ ∞.
Закон распределения (функция вероятности): 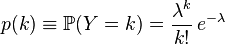
Функции распределения: 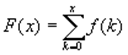
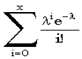
Свойства: Математическое ожидание и дисперсия случайной величины, имеющей распределение Пуассона с параметром λ, равны.
Распределение Пуассона представляет собой вероятностное распределение дискретного типа. Оно моделирует случайную величину, равную числу событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивность и независимы друг от друга.
Выберем фиксированное число λ > 0 и определим дискретное распределение, задаваемое следующей функцией:
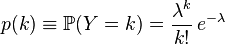
где k! обозначает факториал числа k, e = 2,7182... — основание натурального логарифма
Число событий может принимать целые неотрицательные значения (k = 0, 1, 2,...).
Тот факт, что случайная величина Y имеет случайное распределение Пуассона с параметром λ, записывается как Y ~ P(λ).
Чтобы расcчитать вероятность P (Y = k) необходимо просуммировать все вероятности от нуля до k включительно: P (Y = k) = P (Y = 0) +... P (Y = k).
Распределение Пуассона играет важную роль в теории массового обслуживания, в страховании, теории надежности, теории связи — везде, где в течение определённого времени может происходить случайное число каких-то событий (заявок на обслуживание, страховых случаев, отказов оборудования, телефонных вызовов, радиоактивных распадов, рост числа бактерий в чашке Петри, смертей диктаторов (sic!) и т.д.).
Функция распределения Пуассона относится к гамма-функциям, расширяющим понятие факториала на поле комплексных чисел, и имеет вид
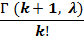
3. Понятие функции распределения. Эмпирическая и теоретическая функция распределения
Функция распределения – определённая функция (частный случай закона распределения), которая описывает область значений случайных величин и вероятности их появления. Так как невозможно перебрать все значения непрерывной случайно величины, то её задают с помощью функции распределения (интегрального закона распределения). Так же с помощью функции распределения можно задать и дискретные распределения (хотя их часто так же задают и схемами, так как область их значений намного меньше непрерывных распределений).
Функцией распределения случайно величины Х называется функция F(x) = P(X < x), где P(X < x) – вероятность того, что случайная величина Х примет значение, меньшее чем х.
Свойства функции распределения:
1. 0 <= F(x) <= 1
2. Вероятность того, что случайная величина Х примет значение из интервала (a;b), равна разности значений функции на концах этого интервала: P(a < X < b) = F(b) – F(a).
3. F(x) – неубывающая функция.
4. 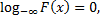
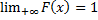
Приложение к 4 свойству:
 (для дискретного распределения)
(для дискретного распределения)
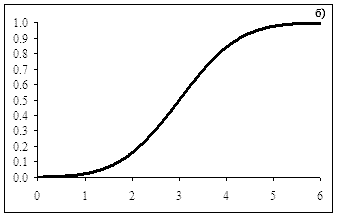 (для непрерывного)
(для непрерывного)
|
| Поделиться: |
Познавательные статьи:
Последнее изменение этой страницы: 2016-04-21; просмотров: 912; Нарушение авторского права страницы; Мы поможем в написании вашей работы!
infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.53.112 (0.011 с.)

 называют функцию
называют функцию 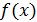 — первую производную от функции распределения
— первую производную от функции распределения  :
: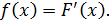
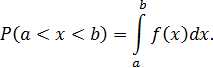


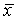 ,
, 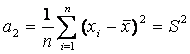
 (17)
(17) i. На основе n выборочных наблюдений оценивается уравнение регрессии
i. На основе n выборочных наблюдений оценивается уравнение регрессии  i =
i =  +
+  +
+  (последний значок означает – при любых i). Требование, означающее несмещенность в среднем «наблюдаемых» значений зависимой переменной относительно «теоретических».
(последний значок означает – при любых i). Требование, означающее несмещенность в среднем «наблюдаемых» значений зависимой переменной относительно «теоретических». , которой не учитывают объясняющие переменные, включённые в уравнение регрессии.
, которой не учитывают объясняющие переменные, включённые в уравнение регрессии.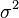 (гомоскедастичность). Не должно быть априорной причины для того, чтобы случайный член порождал бо́льшую ошибку в одних наблюдениях, чем в других. Так как
(гомоскедастичность). Не должно быть априорной причины для того, чтобы случайный член порождал бо́льшую ошибку в одних наблюдениях, чем в других. Так как  равна
равна  , то это условие можно записать так:
, то это условие можно записать так:  (потому что мы знаем, что дисперсия это мат. ожидание в квадрате минус квадрат мат. ожидания). Одна из задач регрессионного анализа состоит в оценке стандартного отклонения случайного члена. Если рассматриваемое условие не выполняется, то коэффициент регрессии, найденные по методу наименьших квадратов, будут неэффективны.
(потому что мы знаем, что дисперсия это мат. ожидание в квадрате минус квадрат мат. ожидания). Одна из задач регрессионного анализа состоит в оценке стандартного отклонения случайного члена. Если рассматриваемое условие не выполняется, то коэффициент регрессии, найденные по методу наименьших квадратов, будут неэффективны. j) = 0
j) = 0  при
при  . Это условие предполагает отсутствие систематической связи между значениями случайного члена в любых двух наблюдениях. Если один случайный член велик и положителен в одном направлении, не должно быть систематической тенденции к тому, что он будет таким же великим и положительным (то же можно сказать и о малых, и об отрицательных остатках).
. Это условие предполагает отсутствие систематической связи между значениями случайного члена в любых двух наблюдениях. Если один случайный член велик и положителен в одном направлении, не должно быть систематической тенденции к тому, что он будет таким же великим и положительным (то же можно сказать и о малых, и об отрицательных остатках). детерминированы и не все равны между собой – Если все
детерминированы и не все равны между собой – Если все  , и в уравнении оценки коэффициента наклона прямой в линейной модели в знаменателе будет ноль, из-за чего будет невозможно оценить коэффициенты β1 и вытекающий из него β0.
, и в уравнении оценки коэффициента наклона прямой в линейной модели в знаменателе будет ноль, из-за чего будет невозможно оценить коэффициенты β1 и вытекающий из него β0. N (β0, I
N (β0, I