
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обзор основных законов распределения, используемых в теории риска.Содержание книги
Поиск на нашем сайте Теория полезности На принятие решения о покупке какого-либо товара влияют следующие основные факторы: · полезность U = f(A,B,C,D) – степень удовлетворения, получаемого субъектом от потребления товара; · цена товара (P); · доход покупателя (I). Потребитель распределяет свои покупки в соответствии с собственными предпочтениями и стремится приобрести на ограниченный доход такой набор благ, который позволил бы ему в максимальной степени удовлетворить потребности. Это достижимо лишь при соблюдении правила максимизации полезности, при котором предельные полезности приобретаемых товаров в расчете на одну денежную единицу оказываются одинаковыми. Кардиналистская (количественная) теория полезности (Е.Бем-Баверк) Предполагала измерение субъективной полезности, или удовлетворения, которую потребитель получает от потребления благ, в зависимости от их потребляемого количества. При росте потребления общая полезность, получаемая от всего объема блага (TU – total utility), растет, а предельная полезность (MU – marginal utility – прирост полезности от потребления дополнительной единицы) падает. Общую полезность можно определить как: TUn = U1 + U2 + … + U n, где U n – полезность последней единицы блага, а n – номер конечного блага в его общем количестве. Соответственно, предельная полезность MUn =TUn — TUn -1, где MUn – приращение полезности, ТUn – общая полезность при потреблении n-го количества блага, а TUn -1 – общая полезность при потреблении предыдущего количества блага. Графически изменения общей и предельной полезности можно изобразить следующим образом:
Предполагается, что можно измерить точную величину полезности, которую потребитель извлекает из потребления блага. Используя количественную теорию полезности, можно охарактеризовать не только общую, но и предельную полезность как дополнительное увеличение уровня благосостояния, получаемого при потреблении дополнительного количества блага данного вида и неизменных количествах потребляемых благ всех остальных видов. Большинство благ обладают свойством убывающей предельной полезности, согласно которому чем больше потребление некоторого блага, тем меньше приращение полезности, получаемой от единичного приращения потребления данного блага. Предельные полезности товаров F, C: При росте количества потребляемого товара предельная полезность каждой дополнительной единицы уменьшается – это закон убывающей предельной полезности.
Закон убывающей полезности нередко называют первым законом Госсена (немецкий экономист ХIХ века), который заключает в себе два положения: 1) убывание полезности последующих единиц блага в одном непрерывном акте потребления, так что в пределе обеспечивается полное насыщение данным благом; 2) убывание полезности каждой единицы блага по сравнению с ее полезностью при первоначальном потреблении. Второй закон Госсена формулирует условия оптимума потребителя: при заданных ценах и бюджете он максимизирует полезность, когда отношение предельной полезности и цены одинаково по всем потребляемым им благам. Из закона следует, что рост цены блага при неизменности цен на все прочие блага и том же доходе вызывает снижение соотношения предельной полезности его потребления и цены, то есть более низкий спрос. Кардиналисты считали, что полезность можно измерить в условных единицах – ютилах. Позднее было доказано, что создать точный количественной измеритель полезности невозможно, и возникла ординалистская (порядковая) теория полезности, включившая в себя положения кардиналистской теории как частный случай.
Согласно ординалистской теории (В.Парето), ценность блага зависит не только от его количества, но и от соотношения с другими благами. Главной задачей покупателя становится выбор из доступных ему по доходу наборов благ набора с наибольшей общей полезностью, то есть оптимизация состава потребительской корзины. Полезность самих потребительских корзин нельзя измерить количественно, их можно ранжировать только качественно, в определенном порядке (ординалистски).
Ординалистский подход к оценке предпочтений потребителя основывается на следующих предположениях: 1) рациональности (транзитивности). Если набор А лучше набора В, а набор В лучше набора С, то набор А предпочтительнее набора С; 2) предпочтения потребителя сформированы и в момент принятия решений не меняются; 3) блага имеют датировку, один и тот же набор в разное время имеет разную полезность; 4) количество блага можно менять непрерывно. В реальности эти предположения могут не соблюдаться. 4. Функция полезности денег. Неравенство Иенсена. Фу́нкция поле́зности — экономическая модель для определения предпочтений экономических субъектов. Основоположное условие концепта функции - рациональное поведение потребителя, выражающееся в выборе из альтернатив тех, которые выводят его на более высокий уровень полезности. Вмикроэкономике концепт функции полезности служит для объяснения поведения потребителей и производителей, в то время как в макроэкономике им пользуются для изображения предпочтений государственных интересов. Первая производнаяфункции полезности по количеству определённого блага Функция полезности (по Нейману) Полезностью варианта xi называется вероятность Ui такая, что ЛПР безразлично получить выигрыш xi наверняка, либо учувствовать в лотерее L(x1,Ui,x2).
Функцией полезности U(x) по Нейману, определенной на упорядоченном по предпочтению множеству Х, называется вероятность U(x)=p(x) такая, что ЛПР безразлично получить x наверняка или учувствовать в лотереи. Функция полезности – действительная функция U(x), определенная на упорядоченном по предпочтительности множестве Х, если она монотонна (
Неравенство Йенсена:
P(x,y) R(x,y) А еще есть рисконейтрал и рискофил:) 5. Понятие лотереи. Детерминированный эквивалент лотереи. Обзор критериев принятия решений в условиях риска. Лотереи: · Простые Вероятностный исход х р y 1-p L(x,p,y) · Сложные L (x1,…,xn,p1,…,pn) Функция полезности (по Нейману) Полезностью варианта xi называется вероятность Ui такая, что ЛПР безразлично получить выигрыш xi наверняка, либо учувствовать в лотерее L(x1,Ui,x2).
Функцией полезности U(x) по Нейману, определенной на упорядоченном по предпочтению множеству Х, называется вероятность U(x)=p(x) такая, что ЛПР безразлично получить x наверняка или учувствовать в лотереи.
Функция полезности – действительная функция U(x), определенная на упорядоченном по предпочтительности множестве Х, если она монотонна (
Ожидаемой полезностью сложной лотереи называется математическое ожидание функции полезности.
Детерминированный эквивалент лотереи – такая величина Определяется из равенства:
Надбавка за риск – величина
При выборе стратегии управления объектом в условиях риска, когда показатели риска характеризуются неопределенностью, заданной интервалом существования риска, возможных ущербов, доходов, в случае спекулятивного риска, могут быть использованы различные критерии выбора стратегии управления риском. К числу этих критериев можно отнести критерий Лапласа, Гурвица, Сэвиджа и Вальда. Критерий Лапласа обычно используется, когда мы не имеем каких либо предпочтений по отношению определенной стратегии управления. В этом случае стратегия может быть определена по средневзвешенному показателю издержек. Критерий Лапласа используется при предположении об известном ЗР издержек на интервале их существования. Если у нас нет представлений о типе этого ЗР, а известен, только интервал существования издержек, то можно считать, что издержки распределены равномерно. Величина издержек управления, на которые мы должны ориентироваться будет определяться из выражения:
f(u) известная плотность их распределения (например равномерный ЗР). Критерий Байеса. Этот критерий применяется при известных вероятностях Pi, и заданной матрице А и характеризует максимальный по всем возможным стратегиям средневзвешенный по вероятностям состояний природы выигрыш игрока. Если средний выйгрыщ при j-й стратегии игрока определяется так
Критерий Лапласа. Этот критерий может рассматриваться как частный случай критерия Байеса в предположении, что все состояния природы равновероятны, т.е. Pi=1/n, i=1,2,…,n. Тогда предыдущее выражение имеет следующий вид:
Критерий Сэвиджа используется, когда требуется выбрать защиту объекта от слишком больших потерь – минимизация потерь для наступления максимально неблагоприятного события.
Критерий Гурвица
Критерий Вальда – используется в случаях, когда речь идет о выборе стратегии управления исходя из требования максимально возможной прибыли в наихудших условиях. Необходимо составить платежную матрицу:
элементы матрицы представляют собой размер выигрыша при реализации j стратегии и наступления неблагоприятного события типа i.
Данный критерий не учитывает распределения неблагоприятных событий, то есть все они предполагаются равновероятными.
6. (Не)склонность ЛПР к риску. Коэффициент неприятия риска Эрроу-Пратта. Связь премии за риск и коэффициента Эрроу-Пратта. (Не)склонность ЛПР к риску описывается коэффициентом неприятия риска Эрроу-Пратта:
7. Проблема выбора в условиях неопределенности и риска как проблема выбора между имеющимися перспективами. (Канеман и Тверски: теория перспектив). Основные эффекты. Функция стоимости в теории перспектив. Теория перспектив предложена Дэниэлом Канеманом и Амосом Тверски в 1979, как обобщение результатов обширных эмпирических наблюдений и эвристических свидетельств; Т.п. - теория принятие решений в усл. неопределенности в 2 этапа: · «редактирование (editing)» вероятностей событий (гипотеза взвешенной вероятности) - преобразование проблемы в совокупность простых перспектив; · «оценка (evaluation)» потерь и выигрышей (гипотеза фабрикации относительной полезности). На первой стадии «редактируются» вероятности событий на основе существующих эвристик и результатов наблюдений, чтобы упростить и облегчить вторую стадию «оценки» потерь и выигрышей.
Функция стоимости: 1) определена на отклонениях от нейтральной точки; 2) вогнута для убытков и выпукла для прибылей; 3) более крута в области убытков нежели в области прибылей.
1)(Эф. отражения) Эффект наверняка. Альтернатива А: 1 шанс из 1000 выиграть 5000 долларов. Альтернатива Б: Получить 5 долларов. Альтернатива В: 1 шанс из 1000 потерять 5000 долларов. t Альтернатива Г: Просто потерять 5 долларов. 80% выбрали альтернативу Г. Канеман и Тверски объяснили это предпочтение тенденцией завышать шансы большой потери по сравнению с большим выигрышем. 2) Эффект убежденности. В случае «вероятностного страхования» испытуемые платят лишь половину взноса, но страхуются лишь в 50% случаев (установка сигнализации, замена старых покрышек, отказ от курения и т.д.). 80% студентов заявили: не воспользуются «вероятностным страхованием», а только полным. (снижение вероятности несчастного случая с изначальной величины (р) до половины (р/2) кажется менее значительным, чем с половины до нуля). Люди предпочитают полностью застраховаться, чем уменьшить возможность катастрофы, даже если выплата будет одинаковой в обоих случаях - маленькая вероятность преувеличивается людьми и таким образом возрастает значение вряд ли возможного события. 3) Функция ценности выпукла вниз (выпукла) для проигрышей и выпукла вверх (вогнута) для выигрышей (причем на участке проигрышей функция значительно круче). Таким образом, имеет место несклонность к риску для выигрышей и склонность к риску для проигрышей (эффект отражения, reflection effect). В случае проигрыша агент теряет в полезности больше, чем он приобрел бы, если бы выиграл аналогичную сумму.
Суть эффекта изоляции заключается в игнорировании при анализе компонентов, которые являются общими для различных перспектив. Эффект игнорирования общих для перспектив составных частей, т. е. общих для перспектив пар исход—вероятность. Например, проблема выбора между перспективами (200, 0,2; 100, 0,5; -50, 0,3) и (200, 0,2; 150, 0,5; -100, 0,3) сводится к проблеме выбора между перспективами (100, 0,5; —50, 0,3) и (150, 0,5; -100, 0,3).
Эффект расположения: Инвесторы менее готовы признать потери (который они были бы вынуждены сделать, если бы они продали активы, которые упали в цене), но более готовы признать прибыль. Это - неразумное поведение, поскольку будущее исполнение акции не связано с ее покупной ценой. Эффект псевдоуверенности: Это относится к тенденции людей чувствовать результат как бесспорный, в то время как фактически это сомнительно. Это наблюдается в многоступенчатых решениях, в которых от оценки результатов на предыдущей стадии решения отказываются, делая выбор на последующих стадиях.(вместо помещения объявления о 25%- ной скидке, химчистка может предложить почистить одну рубашку бесплатно, если уже три сданы в чистку за плату - обслуживание более привлекательно, чем обслуживание со скидкой, даже если это не сказывается на истинной стоимости). Важное следствие теории перспективы (теория оформления сделки) заключается в том, что на способ, которым экономические агенты субъективно, опираясь на собственное мнение, оформляют результат или сделку, влияет субъективная ценность (полезность), которую они ожидают получить.
8. Формула полной вероятности и формула Байеса в оценках риска. Априорная и апостериорная вероятность. Формула полной вероятности и формула Байеса
Если событие А может произойти только при выполнении одного из событий, которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле
Эта формула называется формулой полной вероятности. Вновь рассмотрим полную группу несовместных событий
Если событие А произошло, то это может изменить вероятности гипотез По теореме умножения вероятностей
Откуда
Аналогично, для остальных гипотез
Полученная формула называется формулой Байеса (формулой Бейеса). Вероятности гипотез
Пример. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго - 0,5; для третьего - 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком. Решение. Возможны три гипотезы:
Так как вызов на линию огня любого стрелка равновозможен, то
В результате опыта наблюдалось событие В - после произведенных выстрелов мишень не поражена. Условные вероятности этого события при сделанных гипотезах равны:
по формуле Байеса находим вероятность гипотезы
9. Парадокс Монти Холла (неявное получение дополнительной информации, стратегия перемены решения). Парадокс Монте-Холла Условие: на некотором шоу участнику, дошедшему до финала, предлагается сыграть еще в одну игру. Имеется 3 двери, за одной из них кроется автомобиль, за двумя другими - козел. Участник выбирает одну из дверей, прежде чем ее открыть ведущий открывает одну из тех дверей, за которыми таился козел. После этого ведущий предлагает участнику поменять свой выбор. Вопрос: выгодно ли в такой ситуации менять выбор?
Рассмотрим все возможные исходы: 1) Участник изначально выбрал дверь №1 (козла). В этом случае ведущий открывает дверь 3. Если участник изменяет выбор, он выигрывает. Если нет – проигрывает. 2) Участник выбрал дверь № 2 (автомобиль) 3) Участник выбрал дверь № 3 Таким образом, мы получаем, что следуя стратегии «менять» мы выигрываем в 2-х случаях из трех (т.е. вероятность выигрыша 66,7%, проигрыша – 33,3%). При стратегии «не менять» мы выигрываем в 1-ом случае из трех (вероятность выигрыша 33,3%, проигрыша –66,7%). Окончательно, делаем вывод, что в условиях данной задаче участнику выгодно поменять свой изначальный выбор.
Биномиальный
где p^n - вероятность того, что при n испытаниях событие А наступит n раз; q^n - вероятность того, что при n испытаниях событие А не наступит ни разу;
Мат.ож. = np: Диспр = npq 2) Закон Пуассона - распределение чисел случайного события ni за время t. Вероятность возникновения случайного события n раз за время t
3) Экспоненциальное распределение При определённых допущениях время между появлениями двух последовательных покупателей будет случайной величиной с экспоненциальным распределением. Среднее время ожидания нового покупателя (см. ниже) равно
4) Нормальное распределени е случайной величины X возникает всякий раз, когда X зависит от большого числа однородных по своему влиянию случайных факторов, причем влияние каждого из этих факторов по сравнению с совокупностью всех остальных незначительно. Это условие характерно для времени возникновения отказа, вызванного старением, т.е. этот закон используется для оценки надежности изделий при наличии постепенных (износовых) отказов.
Усеченное нормальное распределение. Так как при нормальном распределении случайная величина может принимать любые значения от -¥ до +¥, а время безотказной работы может быть только положительным, следует рассматривать усеченное нормальное распределение
Логнормальное
Хи квадрат
7) Распределение Вейбулла. Для случая, когда поток отказов не стационарный, т.е. плотность потока изменяется с течением времени.
8) Гамма-распределение случайной величины. Если отказ устройства возникает тогда, когда произойдет не менее k отказов его элементов, а отказы элементов подчинены экспоненциальному закону с параметрами лямбда.
11. Риск и неопределённость. Уровни риска, степени неопределенности. Неопределенность вызывается неполнотой и неточностью информации: - О возможности возникновения неблагоприятного события, его ожидаемой силе, особенностях развития; - О возможной структуре наносимого этим событием ущерба и его величины по каждой составляющей этой структуры; - О влиянии защитных мероприятий на величину возможного ущерба и целым рядом других обстоятельств и факторов. Отличие: Риск появляется тогда, когда существует несколько вариантов развития (альтернатив) событий или есть в наличии статистический опыт определения исходов, т.е. в отличие от неопределенности, риск можно измерить, имея статистические данные Норвежский экономист К. Борх выделил 7 ступеней неопределенности: 1. Нулевая ступень. Для нее характерна строгая детерминированность ситуации, процесса, что, в свою очередь, предопределяет возможность выбора решения на основе прямых расчетов эффективности различных вариантов. Риск отсутствует. 2. Квазидетерминированная неопределенность. Развитие ситуации, а также процессов контролируется, но сроки проявления событий и их сила определены в некоторых диапазонах. Размеры ущерба предсказуемы при различных вариантах стратегий защиты (наводнения, паводки). 3. Стохастическая неопределенность классического типа. Известны законы распределения вероятностей ущерба от ожидаемого негативного события, вероятность его проявления. Характерна для событий с обширной накопленной статистической базой (отказы техники, колебание цен на рынке). 4. Неопределенность с известным распределением событий, но недостаточной выборкой для установления точных значений его параметров. Характерна для редких, но значительных по силе природных и техногенных катастроф, частота и возможный ущерб определяются с некоторой погрешностью. Для таких событий обычно известен тип закона распределения, но его параметры определяются приблизительно (по медиане, отклонению). 5. Неизвестное распределение ущербов при достаточно большой выборке. Например, оценки ущерба, определенные на основе потерь рыночной стоимости, упущенной выгоды. Данные показатели подвержены значительному влиянию конъюнктуры рынка (стоимость с/х продукции, жилого фонда), в свою очередь, зависящей от множества не поддающихся учету факторов. Так, з.р. ущерба часто не удается установить, но можно получить либо оценки погрешностей либо интервальные оценки его характеристик (вероятностей и ущербов). 6. Сильная стохастика событий и малая выборка. Например, техногенные катастрофы на объектах с новой технологией, на которых еще не накоплена статистика отказов оборудования, не выявлены закономерности развития цепи отказов, возможных ущербов. При оценке техногенных рисков тогда используются либо проектные показатели надежности отдельных узлов, либо субъективные оценки характеристик риска, часто в виде интервальных оценок. Эта степень характерна также для политических, межстрановых, социальных рисков. 7. Нестохастическая неопределенность (алеаторная или фортунатная), исключающая какие-либо вероятностные закономерности. Характерна для крайне редких событий (напр., Чернобыльская катастрофа). Ситуация риска наблюдается только с 3-ей степени неопределенности. При первых 2-х неблагоприятное событие является достаточно детерминированным условием. Все остальные степени характеризуют ситуации риска, закономерности и параметры которого могут быть определены с различной степенью достоверности, зависящей от полноты и достоверности исходной информации. Риск – неопределенность в отношении возможных потерь. Уровень риска – определяется отношением величины ущерба к затратам на реализацию и подготовку риск - решения. Измеряется он от нуля до единицы. Если значение выше единицы, то риск считается неоправданным. Теперь, если наугад перебирать все возможности (напр., число покупателей, приходящих за час), сохраняя те же характеристики распределения, можно искусственно воссоздать картину этого процесса. Повторяя такую картину многократно, каждый раз меняя условия (число приходящих покупателей), можно изучать получаемые статистические данные так, как если бы они были получены при наблюдении над реальным потоком покупателей. Точно так же можно воссоздать искусственную картину работы самого магазина: здесь распределение времени подхода покупателей будет взаимодействовать с распределением времени обслуживания отдельного покупателя. Получаются опять два стохастических процесса. Их взаимодействие даст “очередь” с примерно такими же характеристиками (напр., средней длиной очереди или средним временем ожидания), какими обладает реальная очередь.
22. Статистические методы оценки рисков. Статистический метод заключается в изучении статистики потерь и прибылей, которые были на данном или аналогичном предприятии торговли, с целью определения вероятности события и установления величины риска. Вероятность означает возможность получения определенного результата. Например, вероятность успешного продвижения нового товара на рынке товаров и услуг в течение одного года может составить 3/5, а обратная вероятность - 2/5. Величина, или степень, риска измеряется с помощью таких показателей, как среднее ожидаемое значение и колеблемость возможного результата. Средняя величина представляет собой обобщенную количественную характеристику, и по ее значению достаточно трудно принять решение в пользу какого-либо варианта вложения капитала. С этой целью измеряется Колеблемость, или размах, полученного результата. Колеблемость - это степень отклонения ожидаемого значения результата от его средней величины. Для определения колеблемости вычисляют такие статистические величины, как дисперсия и среднее квадратическое отклонение. Дисперсия (σ2) представляет собой среднее взвешенное из квадратов отклонений действительных результатов от средних ожидаемых и рассчитывается по формуле
где х - ожидаемое значение для каждого случая наблюдения;
f- частота случаев или число наблюдений. Дисперсия и среднее квадратическое отклонение являются мерами абсолютной колеблемости. Они измеряются в тех же единицах, что и варьирующий признак. Для анализа степени отклонения часто используется коэффициент вариации. Коэффициент вариации (V)выражается как отношение среднего квадратического отклонения к среднему ожидаемому значению. Он показывает степень отклонения полученных значений и вычисляется по формуле
где σ - среднее квадратическое отклонение;
Коэффициент вариации позволяет сравнивать колеблемость признаков, имеющих разные единицы измерения. Причем чем выше коэффициент вариации, тем сильнее колеблемость признака.
23. Эконометрические методы оценки рисков. Моделирование процесса с помощью корреляционно-регрессионного анализа (построение классич. регрессионных моделей - МНК): а) Трендо-сезонно-циклическая модель б) Модели авторегрессии и скользящей средней в) Метод интерполяции - в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Метод экстраполяции - особый тип аппроксимации, при котором функция аппроксимируется вне заданного интервала, а не между заданными значениями.
Количественный подход позволяет сравнивать различные страны по степени риска, используя единый числовой фактор риска, который суммирует относительное влияние определенного количества социально-политических факторов посредством различных политических и социальных индикаторов. R = R(q1, q2, q3, …, qn) = R(qi), i = 1, …, n, (1) где R — многофакторная функция, зависящая от значений учитываемых факторов qi — совокупность значений i-го фактора Эспертные оценки конечный продукт многоступенчатого консультационного процесса, который может ввязывать либо не ввязывать способ Дельфи. Первая компания - служба BERI (Business Environment Risk Index). Составление рейтинга стран по уровню риска включает в себя несколько этапов: • выбор переменных (политическая стабильность, степень экономического роста, степень инфляции, уровень национализации и др.); • определение веса каждой переменной (максимальный вес имеет переменная политической стабильности); • обр аботка показателей по методу Delphi с использовафнием экспертной шкалы; • выведение суммарного индекса, теоретически располагающегося в пределах от 0 до 100 (минимальный индекс означает максимальный риск, и наоборот). Примеры Примерами операционных рисков являются: · технологические неудачи; · неадекватное хранение документов и записей; · неграмотное управление, недостаток надзора, надежности и контроля; · ошибки в финансовых моделях и отчетах; · попытки скрыть потери или добиться личной выгоды (мошенническая торговля); · мошенничество третьих сторон. Исторически, операционными рисками считались неизбежные издержки ведения бизнеса. Категории рисков Базельский комитет выделил семь основных категорий событий, которые приводят к потерям. Мошенничество внутри компании Потери, связанные с обманом, незаконной собственностью или несоблюдением законов или правил в компании, в которые в
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-24; просмотров: 950; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |

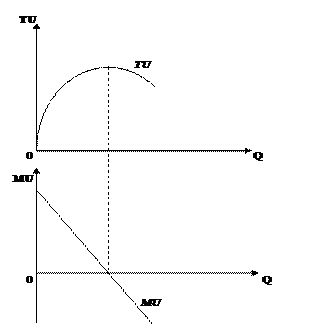
 ;
; 
 называется предельной полезностью этого блага. Предельная полезность выражает, сколько дополнительной полезности приносит дополнительная единица блага
называется предельной полезностью этого блага. Предельная полезность выражает, сколько дополнительной полезности приносит дополнительная единица блага  . Нулевая предельная полезность означает достижение насыщенности. (интернет)
. Нулевая предельная полезность означает достижение насыщенности. (интернет)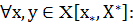 если x предпочтительнее y, то U(x) предпочтительнее U(y))
если x предпочтительнее y, то U(x) предпочтительнее U(y))

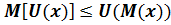 Таким образом, полезность математического ожидания случайного богатства или, что то же самое, полезность безрискового богатства больше математического ожидания полезности случайного богатства. Рискофоб:
Таким образом, полезность математического ожидания случайного богатства или, что то же самое, полезность безрискового богатства больше математического ожидания полезности случайного богатства. Рискофоб:
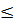 p(x)+p(y)
p(x)+p(y) , что ЛПР безразлично в выборе между участием в лотереи и получением дохода наверняка.
, что ЛПР безразлично в выборе между участием в лотереи и получением дохода наверняка. , следовательно
, следовательно 

 (семинар)
(семинар)
 -средние издержки, обусловленные уровнем риска
-средние издержки, обусловленные уровнем риска  и затратами на его снижение
и затратами на его снижение  .
. -переменные издержки управления.
-переменные издержки управления.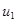 и
и 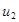 -границы интервала существования издержек
-границы интервала существования издержек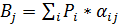 , то оптимальной стратегией
, то оптимальной стратегией  является та, которая обеспечивает максимум этого показателя
является та, которая обеспечивает максимум этого показателя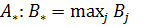 (1)
(1)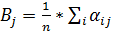 , а оптимальная стратегия определяется выражением (1) (учебник)
, а оптимальная стратегия определяется выражением (1) (учебник) , где
, где 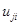 – издержки
– издержки
 .
. – степень оптимизма.
– степень оптимизма. 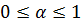
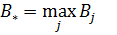

 – т.е выигрыш можно определить как разность между полученным доходом объекта и понесенными издержками. Тогда наилучшая стратегия управления риском по критерию Вальда определяется из условия
– т.е выигрыш можно определить как разность между полученным доходом объекта и понесенными издержками. Тогда наилучшая стратегия управления риском по критерию Вальда определяется из условия  .
.



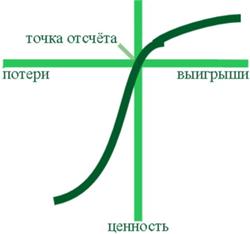 Оценки полезности потерь и выигрышей делаются людьми относительно некоторой точки отсчёта (гипотеза относительной полезности). Функция стоимости, которая проходит через точку отсчёта, имеет асимметричный s-образный вид и показывает, что при одном и том же абсолютном значении ценности воздействие потери сильнее, чем воздействие выигрыша (гипотеза «фабрикации» полезности).
Оценки полезности потерь и выигрышей делаются людьми относительно некоторой точки отсчёта (гипотеза относительной полезности). Функция стоимости, которая проходит через точку отсчёта, имеет асимметричный s-образный вид и показывает, что при одном и том же абсолютном значении ценности воздействие потери сильнее, чем воздействие выигрыша (гипотеза «фабрикации» полезности).

 , вероятности появления которых
, вероятности появления которых 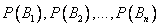 . Событие А может произойти только вместе с каким-либо из событий
. Событие А может произойти только вместе с каким-либо из событий 
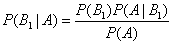

 называются апостериорными вероятностями, тогда как
называются апостериорными вероятностями, тогда как  - априорными вероятностями.
- априорными вероятностями. - на линию огня вызван первый стрелок,
- на линию огня вызван первый стрелок, - на линию огня вызван второй стрелок,
- на линию огня вызван второй стрелок,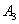 - на линию огня вызван третий стрелок.
- на линию огня вызван третий стрелок.





 ведущий открывает либо дверь 1 либо 3. Если вы соглашаетесь поменять выбор, вы проигрываете. Если не меняете
ведущий открывает либо дверь 1 либо 3. Если вы соглашаетесь поменять выбор, вы проигрываете. Если не меняете  вы выигрываете.
вы выигрываете. открыли дверь № 1. Если меняете выбор
открыли дверь № 1. Если меняете выбор 
 - вероятность того, что при n испытаниях событие А наступит m раз, а событие Ā наступит n-m раз;
- вероятность того, что при n испытаниях событие А наступит m раз, а событие Ā наступит n-m раз; 
 число сочетаний (комбинаций) появления события А и Ā.
число сочетаний (комбинаций) появления события А и Ā.
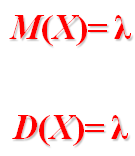
 . Сам параметр
. Сам параметр  тогда может быть интерпретирован как среднее число новых покупателей за единицу времени.
тогда может быть интерпретирован как среднее число новых покупателей за единицу времени.

 мат.ож. = m; диспр = сигма^2
мат.ож. = m; диспр = сигма^2



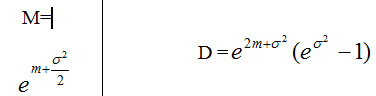




 — среднее ожидаемое значение;
— среднее ожидаемое значение;
 г) Модели с условной гетероскедастичностью (когда дисперсия остатков зависит от квадрата остатков и от дисперсии остатков предыд. мом. времени)(ARCH; GARCH). (фото)
г) Модели с условной гетероскедастичностью (когда дисперсия остатков зависит от квадрата остатков и от дисперсии остатков предыд. мом. времени)(ARCH; GARCH). (фото)


