
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особенности метода моментов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ключевые вопросы: определение, предпосылки модели, понятие и формулы моментов, алгоритм расчёта оценок, применение в нормальном распределении, дискуссия о типе и количестве моментов, достоинства и недостатки подхода. Метод моментов – один из наиболее известных и популярных методов статистического оценивания параметров вероятностных распределений. Основные предпосылки модели метода моментов следующие:
Суть метода моментов заключается в вычислении того количества теоретических и выборочных моментов случайной величины, которое равно числу исследуемых нами параметров. После вычисления соответствующие друг другу теоретические и выборочные моменты приравниваются, и исходя из получившегося уравнения осуществляется вычисление оценки параметра.
Формула выборочных моментов выглядит так: где m’k – есть k-й выборочный момент величины Y.
После этого приравниванием μ’k = m’k добиваемся вычисления значений параметров. Рассмотрим в качестве примера нормальное распределение. Нахождение оценок параметров по методу моментов выглядит следующим образом.
Следует заметить, что в уравнения также допустимо включать и такие экзотические виды моментов, как асимметрию и эксцесс, но это необходимо только в специализированных исследованиях. Статистическая практика чаще всего не выходит за рамки обозначенного выше алгоритма, поскольку число подлежащих исследованию параметров обыкновенно не превышает 4. В качестве достоинств метода моментов следует обозначить, во-первых, то, что его вычислительная реализация сравнительно проста, а, во-вторых, то, что оценки, полученные в качестве решений системы, являются функциями от выборочных моментов, что упрощает исследование статистических свойств оценок данного метода. При больших n распределение оценки такого рода асимптотически нормально, среднее значение отличается от истинного на величину, приблизительно равную n-1, а стандартное отклонение асимптотически равно cn(-1/2), где c – определённая числовая константа. Фишер в своё время доказал, однако, что асимптотическая эффективность оценок по методу моментов всегда оказывается меньше 1, и поэтому данный метод уступает, например, методу максимального правдоподобия. Впрочем, иногда в статистических исследованиях оценки, полученные по методу моментов, принимаются в качестве первого приближения, по которым можно определять другими методами оценки более высокой эффективности.
В другом изложении: Введём сначала следующие определения: Определение 9. Начальный момент порядка k случайной величины x определяется равенством: mk = M(xk). В частности, m1 = M(x) – обычное мат. ожидание, m2 = M(x2). Определение 10. Центральный момент порядка k случайной величины x определяется равенством: ak = M((x–Mx)k). В частности, a2 = D(x) – дисперсия случайной величины. Эти моменты называют теоретическими. По данным наблюдений можно вычислить соответствующие эмпирические моменты: Определение 11. Начальный эмпирический момент порядка k случайной величины x определяется равенством В частности, Определение 12. Центральный эмпирический момент порядка k случайной величины x определяется равенством: В частности, Метод моментов построения точечных оценок неизвестных параметров состоит в приравнивании теоретических моментов рассматриваемого распределения соответствующим эмпирическим моментам того же распределения. Пусть даны: случайная величина ξ, выборка объема n x1, x2,…, xn. Необходимо построить оценки неизвестных параметров q*1,q*2,…,q*k. Описание метода моментов (ММ) разобьём на этапы: 1. Выписываем первые к моментов μ1, μ2, … μn 2. Вычисляем по выборке соответствующие им эмпирические (выборочные) моменты. 3. С оставляем систему уравнений μi = mi и решаем ее относительно неизвестных параметров.
Замечание 1. Иногда вместо начальных моментов μi, mi удобно использовать центральные моменты αi, ai. Замечание 2. Если на третьем этапе получилась неразрешимая система, то на первом шаге надо добавить новые моменты. Найдем методом моментов оценки параметров нескольких важнейших распределений.
|
|||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1663; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.255.181 (0.01 с.) |


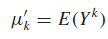 Формула теоретических моментов выглядит так: где μ’k – есть k-й теоретический момент величины Y.
Формула теоретических моментов выглядит так: где μ’k – есть k-й теоретический момент величины Y.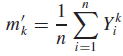
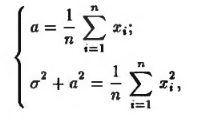
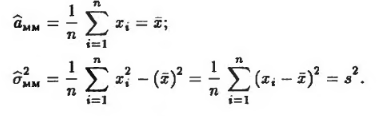
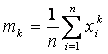
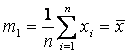 – выборочное среднее.
– выборочное среднее.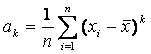
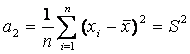 – выборочная дисперсия.
– выборочная дисперсия.


