
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ошибки первого и второго рода: расчет вероятности ошибки первого и второго родаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Проверка статистической гипотезы означает проверку согласования исходных выборочных данных с выдвинутой основной гипотезой. При этом возможно возникновение двух ситуаций – основная гипотеза может подтвердиться, а может и быть опровергнута. Следовательно, при проверке статистических гипотез существует вероятность допустить ошибку, приняв или опровергнув верную гипотезу. При проверке статистических гипотез можно допустить ошибки первого или второго рода Ошибкой первого рода – отвергаем верную гипотезу. Ошибкой второго рода – не отвергаем неверную гипотезу. Уровнем значимости α называется вероятность совершения ошибки первого рода. Значение уровня значимости α обычно задаётся близким к нулю (например, 0,05; 0,01;0,02 и т. д.), потому что чем меньше значение уровня значимости, тем меньше вероятность совершения ошибки первого рода, состоящую в опровержении верной гипотезы Н0. Вероятность совершения ошибки второго рода, т. е. принятия ложной гипотезы, обозначается β При проверке нулевой гипотезы Н0 возможно возникновение следующих ситуаций:
1- β – мощность критерия – способность теста обнаруживать альтернативную гипотезу или способность отвергать Н0, когда верна альтернатива (показывает насколько хороша статистика). Таким образом, чем выше мощность, тем меньше вероятность совершить ошибку второго рода. При проверке гипотез возникают ошибки двух типов. Ошибка первого рода - отвергнуть Н0 , в то время, как она является верной; и ошибка второго рода – принять нулевую гипотезу, которая в действительности является неверной. Вероятность ошибки первого рода называется уровнем значимости и обозначается α. Таким образом, α = Р { U
Уровень значимости ошибки однозначно определен, если гипотеза простая (Н0 : р=1/4, Н1 : р Для проверки как нулевой так и альтернативной гипотезы используется специально подобранная Вероятность ошибки второго рода есть P { U
Поскольку исследователь хочет прийти к правильному выводу, надежные исследования планируются таким образом, чтобы обеспечить низкий уровень а и большую мощность. При низком уровне а крайне мало шансов отвергнуть правильную нулевую гипотезу, а при большой мощности критерия больше шансов принять правильную альтернативную гипотезу. Существует несколько способов увеличить мощность критерия: · Повысить уровень значимомсти. Так повышается вероятность отвергнуть нулевую гипотезу и, соответственно, принять верную альтернативную. Вместе с тем растет риск отвергнуть же нулевую гипотезу, которая может оказаться верной, и совершить таким образом ошибку первого рода. · Формулирование направленных гипотез – исследователь может сосредоточиться на риске с уровнем · Увеличить размер выборки, т.к статистики, основанные на большом количестве респондентов, более устойчивы и обеспечивают более точную оценку характеристик генеральной совокупности. Т.е прибавка прямым образом повышает вероятность того, что будет принята верная гипотеза.
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 10488; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.009 с.) |


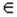 Ψ | H 0}, т.е уровень значимости α – это вероятность события{ U
Ψ | H 0}, т.е уровень значимости α – это вероятность события{ U 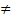 1/4), то есть распределение вероятностей задано точно. Когда же гипотеза сложная, то есть задан тип распределения вероятности с точностью до параметра (Н0 : р=1/4, Н1: р
1/4), то есть распределение вероятностей задано точно. Когда же гипотеза сложная, то есть задан тип распределения вероятности с точностью до параметра (Н0 : р=1/4, Н1: р 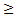 1/4, Н1: р
1/4, Н1: р 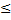 1/4, Н1
1/4, Н1 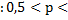 0,8)
0,8)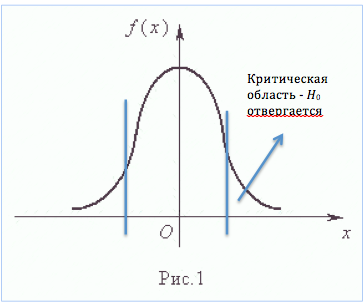 величина, значение которой точно или приближенно известно, соответственно Z – нормальное распределение, F – Фишер, t – Стьюдент,
величина, значение которой точно или приближенно известно, соответственно Z – нормальное распределение, F – Фишер, t – Стьюдент,  2 – «хи-квадрат». После выбора определенного критерия множество всех его возможных значений разделяют на два непересекающихся подмножества: то, где гипотеза принимается, и то, где нет.
2 – «хи-квадрат». После выбора определенного критерия множество всех его возможных значений разделяют на два непересекающихся подмножества: то, где гипотеза принимается, и то, где нет. Ψ | H 1}. Обычно используют не эту вероятность, а а ее дополнение 1, т.е. P { U
Ψ | H 1}. Обычно используют не эту вероятность, а а ее дополнение 1, т.е. P { U 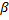 ), где
), где 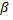 – ошибка второго рода. Стоит отметить, что мощность критерия – достаточно слабая статистика, потому что ошибки в ней слишком часты.
– ошибка второго рода. Стоит отметить, что мощность критерия – достаточно слабая статистика, потому что ошибки в ней слишком часты.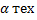 исходов, которые соответствуют выбранной гипотезе.
исходов, которые соответствуют выбранной гипотезе.


