
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ошибки репрезентативности. Ошибки выборкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Любое выборочное наблюдение ставит своей задачей определение среднего размера признака или доли единиц, обладающих данным признаком, и распространение полученных характеристик выборочной совокупности на генеральную совокупность. Ошибки репрезентативности возникают вследствие различия структуры выборочной и генеральной совокупности. Структура генеральной совокупности вполне однозначна, и ей соответствует вполне определенное значение среднего размера (или доли) изучаемого признака. Выборочная же совокупность формируется на основе случайного отбора, в силу этого ее состав отличается от состава генеральной совокупности, отличается, естественно, и значение среднего размера (или доли) изучаемого признака. Если из одной и той же генеральной совокупности производится несколько выборок, то в каждую из них попадут разные единицы и, следовательно, каждой выборочной совокупности будет соответствовать своя средняя. Отсюда следует важный вывод: выборочная средняя, в отличие от генеральной, – величина переменная. Переменной или случайной величиной будет и ошибка репрезентативности. В практических статистических работах выборочное наблюдение проводится один раз, поэтому фактически приходится иметь дело с одной из множества выборочных средних, но с какой именно – сказать невозможно. Чтобы получить суждение о точности результатов выборочного наблюдения, математическая статистика дает формулу средней ошибки, т.е. средней величины из всех возможных ошибок при бесчисленном множестве случайных выборок. При бесконечно большом числе выборок получится кривая частот, которая представляет кривую выборочного распределения. Рассмотрим выборочное распределение средней величины. Такое распределение будет являться нормальным или приближаться к нему по мере увеличения объема выборки независимо от того, имеет или не имеет нормальное распределение та генеральная совокупность, из которой взяты выборки. С увеличением числа выборок средняя для всех выборок будет приближаться к генеральной средней. По выборочному распределению может быть рассчитана средняя квадратическая ошибка репрезентативности:
Среднее квадратическое отклонение выборочных средних от генеральной средней называется средней ошибкой выборочной средней (средней ошибкой выборки для средней величины признака):
Поскольку, как правило, генеральная средняя неизвестна, этой формулой нельзя воспользоваться. Кроме того, в социально-экономических исследованиях выборки из одной и той же совокупности не производятся многократно. Поэтому используют нижеприведенную формулу, исходя из того, что средняя ошибка выборки зависит от колеблемости признака в генеральной совокупности и числа отобранных единиц. Средняя ошибка выборки для средней величины признака определяется по формуле:
где s2г – дисперсия количественного признака в генеральной совокупности. Следовательно, средняя ошибка выборки тем больше, чем больше вариация в генеральной совокупности, и тем меньше, чем больше объем выборки. Т.о. можно утверждать, что отклонение выборочной средней Отношение ошибки конкретной выборки к средней квадратической ошибке называется нормированным отклонением
Распределение нормированного отклонения выборочной средней от генеральной средней при численности выборки
Данное уравнение называют стандартным уравнением нормальной кривой. Величина На рис. приведен график кривой распределения нормированных отклонений ошибок выборочных средних
Рис. Ординаты соответствуют плотностям вероятности при том или ином значении Площадь нормальной кривой, заключенную между ординатами
Имеются таблицы интеграла Лапласа, которые содержат значения вероятностей для нормированных отклонений при t=1 P(D£ m) = Ф(1) = 0,683; при t=2 P(D£2m) = Ф(2) = 0,9545; при t=3 P(D£3m) = Ф(3) = 0,9973 и т.д. Это вероятность того, что ошибка попадет в заданные пределы. В общем виде D=tm характеризует предельную ошибку выборки, показывающую максимально возможное расхождение выборочной и генеральной характеристик при заданной вероятности этого утверждения. Т.о. о величине ошибки можно судить с определенной вероятностью. Так, при t=2 возможная ошибка D не превысит 2m, что гарантируется с вероятностью 0,9545. Это значит, что в 9545 выборках из 10000 подобных максимальная ошибка не выйдет за пределы ±2m, где При проведении выборочного учета массовых социально-экономических явлений считается достаточным максимальный размах ошибки выборки ±3m. На практике наиболее часто пользуются значениями вероятности Р=0,95 (t=1,96), Р=0,99 (t=2,58) и Р=0,999 (t=3,28), гарантирующими репрезентативность выборки соответственно с ошибкой 5; 1; 0,1%. Предельная ошибка выборки позволяет определять предельные значения характеристик генеральной совокупности при заданной вероятности, т.е. их доверительные интервалы. Поэтому вероятность Р называется доверительной, она представляет собой вероятность того, что ошибка выборки не превысит некоторую заданную величину D, т.е. генеральная средняя находится где-то в пределах
генеральная доля – в пределах
Как мы определили выше, средняя ошибка выборки для средней величины признака определяется по формуле:
где s2г – дисперсия количественного признака в генеральной совокупности. Если при выборочном наблюдении изучению подлежит альтернативный признак, то средняя ошибка выборки для доли единиц, обладающих данным признаком, определяется по теореме Я. Бернулли:
где p – доля единиц, обладающих данным качеством, в генеральной совокупности; p(1-p) – дисперсия альтернативного признака в генеральной совокупности.
Приведенные формулы средних ошибок выборки практически непригодны для расчета. В них фигурирует дисперсия признака в генеральной совокупности, которая неизвестна, как неизвестна и генеральная доля, генеральная средняя. Поскольку в теории вероятности доказано, что
то при большом объеме выборки дисперсии генеральной s2г и выборочной s2 совокупностей равны. (
где w – доля признака в выборочной совокупности. Наряду с абсолютной величиной предельной ошибки выборки рассчитывается и относительная ошибка выборки, которая определяется отношением предельной ошибки средней или доли к соответствующей характеристике выборочной совокупности:
При проведении выборочного наблюдения в экономических исследованиях преимущественно стремятся к тому, чтобы относительная ошибка репрезентативности выборки не превышала 5... 10%.
Вывод формул
исходит из схемы повторной выборки. На практике повторная выборка, при которой численность генеральной совокупности остается неизменной (т.е.отобранная единица возвращается в генеральную совокупность и снова может быть отобрана), встречается редко (например, при изучении населения в качестве пользователей, пациентов, избирателей). Обычно отбор организуется по схеме бесповторной выборки, при которой отобранная единица после обследования в генеральную совокупность не возвращается и в дальнейшей выборке не участвует. При бесповторной выборке численность генеральной совокупности в процессе отбора сокращается на 1–n/N, где n/N – доля отобранных единиц. В связи с этим формулы ошибки выборки приобретают следующий вид:
Так как доля единиц генеральной совокупности, не попавших в выборку (1–n/N), всегда меньше единицы, то ошибка выборки при бесповторном отборе при прочих равных условиях меньше, чем при повторном отборе.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1997; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.239.50 (0.007 с.) |

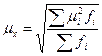 ,
,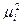 - квадрат ошибки репрезентативности для i-й выборки,
- квадрат ошибки репрезентативности для i-й выборки,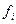 - число выборок с одинаковым значением выборочной средней.
- число выборок с одинаковым значением выборочной средней.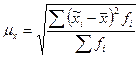 /
/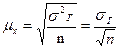 ,
,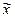 от генеральной средней
от генеральной средней 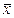 в среднем равно
в среднем равно 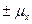 . Ошибка конкретной выборки может принимать различные значения, но ее отношение к средней ошибке практически не превышает
. Ошибка конкретной выборки может принимать различные значения, но ее отношение к средней ошибке практически не превышает 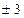 , если величина объема выборки достаточно большая
, если величина объема выборки достаточно большая 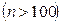 .
. :
: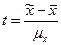 .
.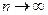 определяется следующим уравнением:
определяется следующим уравнением: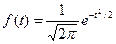 (1)
(1) достигает максимума при
достигает максимума при 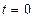 , в этом случае
, в этом случае 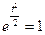 .
.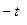 до
до 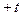 , следует найти отношение части площади кривой, заключенной между ординатами, соответствующими
, следует найти отношение части площади кривой, заключенной между ординатами, соответствующими 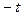 и
и 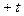 ко всей площади кривой. Вся площадь под кривой нормального распределения вероятностей принимается за единицу.
ко всей площади кривой. Вся площадь под кривой нормального распределения вероятностей принимается за единицу.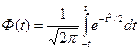
 – это коэффициент доверия.
– это коэффициент доверия.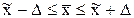 (от
(от 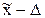 до
до  ),
),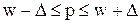 (от w–D до w+D).
(от w–D до w+D). ,
,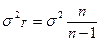 ,
,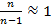 ). Это дает основание исчислять среднюю ошибку выборки по значениям выборочной дисперсии s2 для средней и w(1–w) для доли признака:
). Это дает основание исчислять среднюю ошибку выборки по значениям выборочной дисперсии s2 для средней и w(1–w) для доли признака: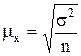 ,
, 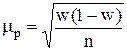 ,
,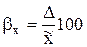 ;
; 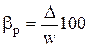 .
.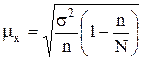 ;
; 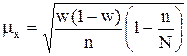 .
.


