
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы выявления корреляционной связиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Наиболее простым и эффективным способом выявления взаимосвязей между явлениями, с которого начинается корреляционный анализ, является графический метод. Для этого на координатном поле наносят точки, соответствующие значениям изучаемых признаков x и y. На оси абсцисс откладывают значения факторного признака х, на оси ординат – результативного признака y. Совокупность точек образует корреляционное поле. По характеру расположения точек на корреляционном поле можно судить о направлении и силе связи. Если точки беспорядочно разбросаны по полю, то зависимость между переменными отсутствует; если точки образуют эллипс, т.е. концентрируются вокруг оси, идущей из нижнего левого угла в верхний правый (или наоборот), то имеется прямая (или обратная) зависимость между исследуемыми признаками.
Следующий метод выявления взаимосвязи между явлениями – метод сравнения параллельных рядов. Сущность метода сравнения параллельных рядов состоит в сопоставлении рядов, ранжированных по факторным признакам. Для этого все единицы исследуемой совокупности располагают в возрастающем или убывающем порядке по уровню факторного признака, параллельно располагают значения результативного признака. Посредством сопоставления расположенных таким образом рядов выявляется наличие связи и ее направление. Такое субъективное суждение о наличии корреляционной связи сопровождается расчетом того или иного показателя тесноты связи. Простейшим показателем тесноты связи является коэффициент Фехнера. Коэффициент Фехнера КФ (коэффициент корреляции знаков) оценивает направление и тесноту связи на основе сравнения знаков отклонений значений результативного y и факторного х признаков от их средних арифметических: КФ где С – число совпадений знаков отклонений y от Т.о. во внимание принимаются не величины отклонений от средней, а их знаки (+,-). Совпадение знаков отклонений по обоим признакам означает согласованную вариацию, несовпадение – нарушение согласованной изменчивости. Коэффициент Фехнера изменяется от –1 до +1. При КФ = +1 имеет место согласованная изменчивость, при КФ = –1 – обратная изменчивость, при КФ = 0 – согласованная изменчивость отсутствует. Этот коэффициент улавливает наличие и направление связи, но не учитывает тесноту связи. Метод группировок При большом числе наблюдений для выявления корреляционной связи между двумя количественными признаками удобно пользоваться методом группировок. К важнейшим приемам выявления зависимостей между признаками относится метод аналитических группировок. Аналитические группировки служат основой для характеристикивзаимосвязи между явлениями. Аналитические группировки дают возможность проявиться взаимосвязи следующим образом: с возрастанием значения факторного признака систематически возрастает или убывает среднее значение результативного. С помощью аналитических группировок можно изучить всё многообразие связей и зависимостей между варьирующими признаками. Преимущество метода аналитических группировок по сравнению с другими методами анализа связей (например, корреляционного, дисперсионного) состоит в том, что единственным условием для его применения является однородность исследуемой совокупности. Результаты группировки единиц совокупности могут быть представлены по-другому: в виде таблицы, в которой приведено комбинационное распределение единиц совокупности по двум и более признакам. Такие таблицы называют таблицами взаимной сопряженности. Если в таблице оба признака, по которым дано распределение единиц совокупности, количественные, то такая таблица взаимной сопряженности называется корреляционной. Корреляционная таблица строится по типу «шахматной». О наличии и направлении связи можно судить по внешнему виду таблицы, т.е. по расположению в ней частот. На основе аналитических группировок и корреляционных таблиц можно не только выявить наличие зависимости между двумя показателями, но и измерить тесноту этой связи. Для оценки тесноты связи между двумя признаками исчисляется эмпирическое корреляционное отношение h, равное корню квадратному из частного межгрупповой дисперсии к общей дисперсии:
Коэффициент детерминации h2=d2/s2 показывает, какая часть общей вариации результативного признака объясняется вариацией факторного (группировочного) признака.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1400; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.89.130 (0.007 с.) |

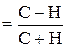 ,
, и х от
и х от 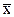 по всем единицам изучаемой совокупности; Н – число случаев несовпадений знаков отклонений.
по всем единицам изучаемой совокупности; Н – число случаев несовпадений знаков отклонений.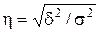 .
.


