
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение роли отдельных факторов в динамике результативных показателейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При изучении динамики количественных и качественных показателей возникает потребность измерения влияния отдельных факторов на совокупное изменение результативного показателя, т.е. оценить, как изменился этот показатель в результате изменения каждого фактора в отдельности, в том числе структуры социально-экономического явления. Влияние отдельных факторов оценивается с помощью индексного метода, основанного на построении системы взаимосвязанных индексов. Индексный метод факторного анализа может применяться только в тех случаях, когда между результативными и факторными показателями имеется функциональная связь. Система взаимосвязанных индексов должна выразить индекс результативного показателя в виде математической зависимости индексов факторных показателей. Например, динамика стоимости продукции обусловлена совместным изменением количества различных видов продукции и цен на отдельные их виды. Индекс динамики стоимости продукции, в котором переменными величинами являются и цены и количества услуг, равен произведению индексов цен (где переменные только цены) и физического объема (переменные только количества отдельных видов продукции):
Следует еще раз подчеркнуть, что взаимосвязь общих индексов осуществляется при условии экономически обоснованного выбора весов (соизмерителей) индексов и таким образом, чтобы не нарушалась алгебраическая взаимосвязь показателей, входящих в единую систему. Например, если в качестве весов индекса цен и физического объема приняты величины отчетного периода, то искомый индекс стоимости не получится:
Влияние отдельных факторов на абсолютное изменение результативного показателя определяется на основе разностей между числителем и знаменателем взаимосвязанных индексов. По аналогии с рассмотренными взаимосвязанными индексами стоимости продукции (услуг, товарооборота), физического объема продукции (услуг) и цен Iqp = Iq∙Ip можно построить систему взаимосвязанных индексов издержек производства, физического объема продукции (услуг) и себестоимости продукции (услуг) Iэ = Iq ∙ Ic
где с0, с1 – себестоимость продукции (услуг) в базисном, отчетном периодах;
Экономическая наука и практика широко пользуется исследованием явлений, находящихся в функциональной зависимости.
Например, взаимосвязаны между собой объем услуг (доходы) предприятия, производительность труда и численность работников (D = W∙T); затраты на производство, себестоимость и объем услуг (Э = c∙Q); фонд заработной платы, средняя заработная плата и численность работников (З = з∙Т). Если взять отношения каждой из этих зависимостей за два периода, то получатся аналогичные выражения для взаимосвязанных индексов: ID = IW∙IT; IЭ = Ic∙IQ; IЗ = Iз∙IТ. Такие системы привлекаются для расчетов одного из показателей, входящих в систему, если известны два других. Например, известно, что себестоимость продукции предприятия снизилась на 6%, объем продукции в денежном выражении увеличился на 15%. Зная, что динамика затрат на производство IЭ определяется произведением индексов себестоимости услуг Iс и объема услуг IQ, можно легко узнать, как изменятся издержки производства в данном предприятии: IЭ=Ic∙IQ=0,94×1,15=1,081, т.е. они увеличатся на 8,1%.
Системы взаимосвязанных индексов применяются также при анализе и изучении факторов прироста. Рассмотрим данный вопрос на примере анализа прироста доходов за счет двух факторов: изменения производительности труда и изменения численности работников.
Какова же степень влияния изменения производительности труда и численности работников на общий прирост доходов? Для ответа на этот вопрос используется специальный прием, который называется методом цепной подстановки. Суть его состоит в пошаговом переходе от базисного значения результативного показателя к отчетному путем последовательной (цепной) замены базисных значений факторов на отчетные.
Можно определить относительные размеры прироста доходов по факторам в общем приросте: долю прироста доходов за счет роста производительности труда Метод цепной подстановки требует соблюдения следующего правила: подстановка отчетных данных вместо базисных начинается с количественного (экстенсивного) фактора и заканчивается качественным (интенсивным) фактором. Второй метод изучения роли влияния отдельных факторов основывается на рассмотренной выше взаимосвязанной системе индексов переменного, постоянного состава и структурных сдвигов.
Рассмотрим его на примере взаимосвязанных индексов Iqp, Iq, Ip . Средняя цена на продукцию в отчетном и базисном периоде определяется:
Тогда стоимость продукции в отчетном и базисном периоде составит
Следовательно, изменение стоимости можно представить как результат изменения средней цены
Т.о. абсолютный прирост стоимости (доходов) как результативного показателя
складывается из приростов по отдельным факторам 1) за счет изменения объемов продаж
2) за счет изменения средней цены на продукцию
Однако изменение средней цены зависит от изменения цен и доли реализации продукции на отдельных рынках. Поэтому абсолютный прирост доходов за счет изменения средней цены можно в свою очередь подразделить на две части. 1) прирост доходов за счет изменения цен на отдельных рынках
2) прирост доходов за счет изменения структуры (доли) продаж на отдельных рынках
Территориальные индексы В статистике для сопоставления экономических показателей в пространстве: по регионам, экономическим районам, федеральным округам, используются территориальные индексы. При построении территориальных индексов главной методологической задачей является выбор весов, т.е. какие веса использовать для расчетов: первого региона (А), второго региона (Б) или области (экономического района, округа) (А+Б), в которой находятся оба региона. Если взять один из регионов в качестве базы сравнения, то можно построить два индекса (на примере индекса цен):
и получить различное представление о соотношении уровней изучаемого явления. Если значения индексируемого признака взвешиваются не по весам какого-то одного региона, а по весам области, в которой находятся сравниваемые регионы, то используется метод стандартных весов:
Для пространственного сопоставления широко применяется рассмотренный ранее индекс Фишера.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 691; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.101.231 (0.01 с.) |

 .
. , т.е. I'q ∙ I'p ¹ Iqp.
, т.е. I'q ∙ I'p ¹ Iqp. ,
, 
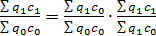 ,
, ,
, 
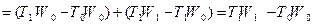
 и долю прироста доходов за счет увеличения численности работников
и долю прироста доходов за счет увеличения численности работников  .
. ,
, 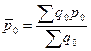


 и изменения общего объема проданной продукции
и изменения общего объема проданной продукции 










 .
.


