
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретическое корреляционное отношениеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Показателями тесноты корреляционной связи служат коэффициент и индекс корреляции. Теснота связи между признаками измеряется с помощью показателей вариации результативного признака y. Обратимся к рис. 8.1, на котором изображены три линии: y – ломаная, называемая эмпирической линией регрессии, которая отражает фактические значения y при соответствующих значениях факторного признака х;
Поскольку на y помимо х оказывают влияние и другие факторы, то линия y не совпадает с линией Чтобы измерить, насколько связь близка к функциональной, исчисляют показатели тесноты связи. Для этого необходимо оценить вариацию результативного признака y, вызванную только влиянием признака х, и остаточную его вариацию, обусловленную прочими факторами. Общая дисперсия результативного признака характеризует вариацию y под влиянием всех факторов. Средний квадрат отклонений измеряет вариацию y только под влиянием фактора х – это факторная дисперсия. Средний квадрат отклонений y от
характеризует остаточную вариацию y под влиянием всех остальных факторов. В математической статистике доказано, что s2y = Поэтому эту дисперсию называют остаточной дисперсией, она характеризует вариацию y за счет остальных факторов, не включенных в уравнение регрессии. Теснота связи между y и х измеряется отношением факторной дисперсии к общей дисперсии результативного признака, называемым теоретическим индексом детерминации,
Теоретический индекс детерминации характеризует долю вариации результативного признака под влиянием факторного признака в общей колеблемости результативного признака. Если между признаками имеется корреляционная связь, то по мере ее усиления, т.е. повышения тесноты связи между результативным и факторным признаками, индекс детерминации увеличивается, а по мере ослабления – уменьшается. Таким образом, индекс детерминации характеризует тесноту связи, близость корреляционной связи к функциональной. Корень квадратный из индекса детерминации есть индекс корреляции или теоретическое корреляционное отношение. Индекс корреляции, или теоретическое корреляционное отношение, характеризует тесноту связи при любой форме зависимости. Остаточная дисперсия
Частным случаем индекса корреляции является линейный коэффициент корреляции r, который применяется для оценки тесноты связи при линейной зависимости. При прямолинейной связи линейный коэффициент корреляции тождествен индексу корреляции, они численно равны: Корреляционное отношение – универсальный показатель, применимое ко всем случаям корреляционной зависимости независимо от формы этой связи. Следует различать эмпирическое и теоретическое корреляционное отношение. Эмпирическое корреляционное отношение рассчитывается по аналитической группировке (или корреляционной таблице) как корень квадратный из отношения межгрупповой дисперсии результативного признака к общей дисперсии результативного признака. Теоретическое корреляционное определяется на основе выровненных (теоретических) значений результативного признака, рассчитанных по уравнению регрессии (для любой формы связи). Эмпирическое и теоретическое корреляционное отношение определяются по формулам:
где
Множественная корреляция
Задача многофакторного корреляционно-регрессионного анализа заключается, во-первых, в изучении целого ряда факторов, влияющих на исследуемый показатель и отборе наиболее значимых; во-вторых, в определении степени влияния каждого фактора на результативный признак путем построения модели – уравнения множественной регрессии, которая позволяет установить, в каком направлении и на какую величину изменится результативный показатель при изменении каждого фактора, входящего в модель; в-третьих, в количественной оценке тесноты связи между результативным признаком и факторными. Математически задача состоит в нахождении аналитического выражения, наилучшим образом отражающего связь факторных признаков с результативным, т.е. в нахождении функции
Выбор формы уравнения множественной регрессии осуществляется на практике на основе использования пяти типов моделей: линейная степенная показательная параболическая гиперболическая Чаще всего останавливаются на линейных моделях. Это объясняется тем, что, во-первых, параметры линейных уравнений легко интерпретируются, сами модели просты и удобны для экономического анализа, во-вторых, при желании любую функцию путем логарифмирования или замены переменных можно свести к линейной форме. В уравнении множественной регрессии в линейной форме параметры а1, а2, а3,..., аn – коэффициенты регрессии, показывают степень влияния соответствующих факторов на результативный признак при закреплении остальных факторов на среднем уровне, т.е. насколько изменится y при увеличении соответствующего фактора на 1 пункт его единицы изменения; параметр а0 – свободный член, экономического смысла не имеет. Выбор формы уравнения множественной регрессии основывается на теоретическом анализе изучаемого явления. Если анализ взаимосвязей результативного и факторных признаков не позволяет остановиться на какой-либо форме связи, то перебирают различные функции и выбирают оптимальную с точки зрения близости эмпирических значений результативного признака выровненным.
Параметры уравнения множественной регрессии рассчитываются методом наименьших квадратов на основе решения системы нормальных уравнений. Для линейного уравнения регрессии с n факторами строится система из (n+1) нормальных уравнений:
a0Sx1 + a1Sx21 + a2Sx1x2 +...+ anSx1xn = Syx1, : a0Sxn + a1Sx1xn + a2Sx2xn +...+ anSx2n = Syxn. Поскольку коэффициенты регрессии между собой несопоставимы (факторы имеют разные единицы измерения), то нельзя сравнивать силу влияния каждого из включенных в модель факторов на результативный признак на основании коэффициентов регрессии. В целях перехода от натурального масштаба переменных
При переходе к стандартизированному масштабу переменных уравнение множественной регрессии принимает вид
где b-коэффициент показывает, на какую часть среднего квадратического отклонения
где sxi, sy – средние квадратические отклонения i-го фактора и результативного признака. Кроме того, Параметры уравнения множественной регрессии в натуральном масштабе и уравнения регрессии в стандартизированном виде взаимосвязаны:
Для оценки сравнительной силы влияния факторов рассчитывают также частные коэффициенты эластичности. Частный коэффициент эластичности показывает, на сколько процентов в среднем изменится результативный показатель при изменении фактора на 1% и фиксированном положении других факторов и рассчитываются отдельно по каждому фактору:
где аi – коэффициент регрессии при i-м факторе;
Вследствие того, что экономические явления подвергаются воздействию многочисленных и сложных причин, в уравнение множественной регрессии должны включаться существенные, систематически действующие факторы при элиминировании влияния остальных факторов. Наиболее важные факторы отбираются на основе анализа тесноты и существенности связи между факторами и результативным показателем. При этом условием включения в модель факторов является отсутствие между ними очень тесной корреляционной связи, близкой к функциональной. Наличие между двумя факторами весьма тесной линейной связи (линейный коэффициент корреляции r превышает по абсолютной величине 0,85) называется коллинеарностью, а между несколькими факторами – мультиколлинеарностью. Причины возникновения мультиколлинеарности между признаками состоят, во-первых, в том, что анализируемые признаки характеризуют одну и ту же сторону явления или процесса (например, уставной фонд и численность работников характеризуют размер предприятия) и включать их в модель одновременно нецелесообразно; во-вторых, факторные признаки являются составными элементами друг друга, дублируют друг друга или их суммарное значение дает постоянную величину (например, энерговооруженность и фондовооруженность, удельный вес заемных и собственных средств). Если в модель включены мультиколлинеарные факторы, то уравнение регрессии будет неадекватно отражать реальные экономические взаимосвязи, будут искажены величины параметров модели (завышены), изменен смысл и затруднена экономическая интерпретация коэффициентов регрессии и корреляции. Поэтому при построении модели исключают один из коллинеарных факторов исходя из качественного и логического анализа или преобразуют исходные факторные признаки в новые, укрупненные. Качество и адекватность модели реальному социально-экономическому явлению и процессу определяется оптимальностью числа факторных признаков: чем больше включается факторов, тем модель лучше описывает явление и процесс, но такую модель трудно реализовать; при малом числе факторов модель недостаточно адекватна.
Многофакторная система требует уже не одного, а множества показателей тесноты связей, имеющих разный смысл и применение. Теснота связи между изучаемыми показателями при множественной корреляции определяется на основе различных коэффициентов: 1) парные коэффициенты корреляции r измеряют тесноту линейной связи между факторами и между результативным признаком и каждым из рассматриваемых факторов без учета их взаимодействия с другими факторами. Строится матрица парных коэффициентов корреляции. Матрицу можно использовать для предварительного отбора факторов для включения их в уравнение регрессии. Матрица парных коэффициентов корреляции
2) совокупный коэффициент детерминации
3) совокупный коэффициент множественной корреляции
где Чем меньше эмпирические значения результативного признака отличаются от выровненных по линии множественной регрессии, тем корреляционная связь между исследуемыми показателями теснее и совокупный коэффициент множественной корреляции ближе к единице. Совокупный коэффициент множественной корреляции зависит не только от корреляции результативного признака с факторными, но и от корреляции факторных признаков между собой. В случае двухфакторной модели совокупный коэффициент множественной корреляции может быть определен через парные коэффициенты корреляции и рассчитывается по формуле:
4) частные коэффициенты детерминации характеризуют степень влияния факторов на результативный признак при элиминировании их взаимосвязи с остальными (что возможно, когда остальные факторы закреплены на постоянном уровне):
где
Частный коэффициент детерминации характеризует долю вариации результативного признака, обусловленную воздействием данного фактора, при элиминировании его взаимосвязи с остальными факторами, включенными в анализ. Следует помнить, что коэффициенты частной детерминации – это доли от разных величин, поэтому они несравнимы, по этим долям нельзя судить о роли факторов. Их главное практическое значение – определить, имеет ли смысл добавить в уравнение регрессии новый фактор или нет. Если при его включении ранее необъясненная вариация уменьшится на 3/4, его включение оправдано; если же коэффициент частной детерминации мал, то дополнительный фактор включать не следует. В зависимости от количества факторов, влияние которых исключается, частные коэффициенты детерминацииции могут быть первого порядка (при исключении влияния одного фактора), второго порядка (при исключении влияния двух факторов) и т.д.
Частный коэффициент корреляции – корень квадратный из частного коэффициента детерминации. Частный коэффициент корреляции первого порядка между y и х1 при исключении влияния х2 в двухфакторной модели рассчитывается по формуле:
где ryx1, ryx2, rx1x2– парные коэффициенты корреляции между соответствующими признаками.
Ряды динамики
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 2382; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.53.90 (0.013 с.) |

 – прямая линия, параллельная оси абсцисс, соответствующая среднему значению y при исключении влияния всех факторов;
– прямая линия, параллельная оси абсцисс, соответствующая среднему значению y при исключении влияния всех факторов; – выравненная линия регрессии, характеризующая значения y при абстрагировании всех факторов, кроме фактора х.
– выравненная линия регрессии, характеризующая значения y при абстрагировании всех факторов, кроме фактора х.
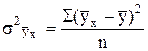
 = S(y–
= S(y–  , т.е.
, т.е.  .
. .
. .
. .
. ,
, 
 - число групп по факторному признаку,
- число групп по факторному признаку, 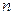 - число единиц совокупности,
- число единиц совокупности,  - среднее значение признака
- среднее значение признака  в
в  -й группе;
-й группе; - значение
- значение  -й единицы совокупности, рассчитанное по уравнению регрессии.
-й единицы совокупности, рассчитанное по уравнению регрессии. = f(x1,x2,x3,...,xn).
= f(x1,x2,x3,...,xn). a0 + a1x1 + a2x2 +... +anxn;
a0 + a1x1 + a2x2 +... +anxn; ;
; ;
;

 a0n + a1Sx1 + a2Sx2 +...+ anSxn = Sy,
a0n + a1Sx1 + a2Sx2 +...+ anSxn = Sy, к центрированным и нормированным отклонениям
к центрированным и нормированным отклонениям  , проводится процедура стандартизации переменных.
, проводится процедура стандартизации переменных. ,
,  ,
,  ,
, 
 ,
, - коэффициенты регрессии.
- коэффициенты регрессии. изменяется результативный признак при изменении соответствующего фактора на величину его среднего квадратического отклонения
изменяется результативный признак при изменении соответствующего фактора на величину его среднего квадратического отклонения  , а прочие факторы не изменились
, а прочие факторы не изменились ,
,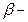 коэффициенты позволяют оценить степень воздействия факторных признаков на результат. Т.к. все
коэффициенты позволяют оценить степень воздействия факторных признаков на результат. Т.к. все  фактор
фактор  сильнее влияет на результативный признак, чем фактор
сильнее влияет на результативный признак, чем фактор  .
.
 ,
, – среднее значение i-го фактора;
– среднее значение i-го фактора; 







 характеризует долю вариации результативного признака, обусловленную изменением всех факторов, входящих в уревнение множественной регрессии. Совокупный коэффициент детерминации характеризует тесноту связи между результативным признаком и всеми факторами независимо от формы связи (линейной или нелинейной):
характеризует долю вариации результативного признака, обусловленную изменением всех факторов, входящих в уревнение множественной регрессии. Совокупный коэффициент детерминации характеризует тесноту связи между результативным признаком и всеми факторами независимо от формы связи (линейной или нелинейной): , или
, или 
 представляет собой квадратный корень из совокупного коэффициента детерминации
представляет собой квадратный корень из совокупного коэффициента детерминации 
 =
=  ,
, – дисперсия результативного признака под влиянием факторов, включенных в модель;
– дисперсия результативного признака под влиянием факторов, включенных в модель;  – остаточная дисперсия результативного признака, вызванная влиянием не учтенных моделью факторов.
– остаточная дисперсия результативного признака, вызванная влиянием не учтенных моделью факторов. 
 .
.
 ,
, - коэффициент множественной детерминации, отражающий влияние всех включенных в анализ факторов,
- коэффициент множественной детерминации, отражающий влияние всех включенных в анализ факторов, - коэффициент множественной детерминации, отражающий влияние всех факторов, кроме одного, воздействие которого отражает частный коэффициент детерминации.
- коэффициент множественной детерминации, отражающий влияние всех факторов, кроме одного, воздействие которого отражает частный коэффициент детерминации. ,
,


