
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы выявления основной тенденции в рядах динамикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Одна из важнейших задач изучения рядов динамики – выявить основную тенденцию (закономерность) в изменении уровней ряда, называемую трендом. Закономерность в изменении уровней ряда в одних случаях проявляется довольно наглядно, в других – может затушевываться колебаниями, вызванными случайными и неслучайными причинами. Можно сказать, что динамика ряда включает три компоненты: • долговременное движение (тренд), • кратковременное систематическое движение (например, сезонные колебания), • несистематическое случайное движение, вызывающее колебания уровней относительно тренда. Изучая ряды динамики, исследователи пытаются разделить эти компоненты и выявить основную закономерность развития явления в отдельные периоды, освобожденную от действия случайных факторов. Для этого ряды динамики подвергают обработке. Статистическая наука применяет ряд методов преобразования рядов динамики, позволяющих обнаружить и показать основную тенденцию в развитии явления. Метод укрупненных интервалов Наиболее простым является метод укрупнения интервалов. Укрупнение периодов является простейшим методом преобразования рядов динамики. Чаще всего им пользуются, когда анализируют данные об изменении явления внутри года: суточные, недельные, месячные. Сглаживание ряда с помощью скользящей средней Другим методом преобразования рядов динамики является их сглаживание с помощью скользящей средней. Этот метод состоит в последовательном вычислении средних величин по определенному числу уровней ряда динамики, причем при вычислении каждой новой средней отбрасывается один уровень ряда слева и присоединяется один уровень ряда справа. Скользящая средняя может быть вычислена по трем, четырем, пяти и т.д. членам ряда динамики. Рассчитанные из нескольких членов ряда скользящие средние относятся к середине (центру) каждого рассматриваемого интервала. Сглаживание рядов методом скользящей средней можно проводить по любому числу членов ряда Недостатком метода скользящей средней является то, что сглаженный ряд «укорачивается» по сравнению с фактическим с двух концов. Метод скользящей средней сглаживает лишь случайные колебания, если же ряд содержит сезонную волну, то она сохранится и после сглаживания.
Аналитическое выравнивание рядов динамики Более совершенный метод обработки рядов динамики в целях устранения случайных колебаний и выявления тренда – метод аналитического выравнивания рядов динамики. При этом способе общее направление в развитии явления выражается плавно изменяющейся линией – трендом, характеризующим тенденцию его динамики. Суть метода – замена эмпирических уровней При этом каждый фактический уровень
где
Аналитическая формула этой линии устанавливается математическими методами, при этом выбор формы кривой должен быть обоснован экономически. Выравнивание может быть произведено по линейной или нелинейной зависимости, выражающей функциональную зависимость уровней ряда динамики от времени: Выбор аналитической функции может осуществляться на основе графического изображения ряда. Вспомогательную роль при выборе функции играют механические приемы сглаживания (укрупнение интервалов, метод скользящей средней). Они частично устраняют случайные колебания. При выборе аналитической функции для выравнивания ряда динамики можно использовать метод конечных разностей:
1-е разности 2-е разности 3-е разности
В результате многолетнего опыта выравнивания рядов динамики наработаны следующие условия использования того или иного вида аналитических функций: 1. Если первые разности приблизительно равны
2. Если постоянны вторые разности
Если постоянны n-е разности уровней, то можно использовать параболу n-го порядка
3. если значения уровней меняются в геометрической прогрессии, т.е. цепные темпы роста приблизительно постоянны
4. если обнаружено замедленное снижение уровней ряда, которые по логике не могут снизиться до нуля, для описания тренда выбирают гиперболу
5. если наблюдается периодичность изменения уровней и их можно представить в виде синусоидальных колебаний, используется ряд Фурье
где k – число гармоник (гармоники – синусоиды, полученные при выравнивании по ряду Фурье). Имеется множество других аналитических функций для выравнивания рядов динамики. Если уровни ряда трудно математически описать одной функцией, следует разбить ряд на отдельные части и выравнивать каждую часть по своей функции.
В приведенных уравнениях В статистической практике параметры уравнений интерпретируются следующим образом: a0 – характеризует средние условия ряда динамики, а1 – изменение скорости (ускорения), в линейной функции показывает, на сколько изменится уровень ряда при изменении единицы времени на единицу. Задача аналитического выравнивания сводится к тому, чтобы фактические значения ряда динамики y заменить теоретическими Для нахождения параметров уравнений методом наименьших квадратов решается система нормальных уравнений. МНК Рассмотрим определение параметров уравнения МНК для линейной функции Для уравнения прямой строится следующая система:
a0St + a1St2 = Syt, где n – число уровней ряда; t – показатель времени, обозначаемый порядковыми номерами, начиная с низшего, например: t = 1, 2, 3, 4... Решение системы нормальных уравнений позволяет получить выражение для параметров a0 и a1:
Так как в рядах динамики значения t являются показателями времени, то всегда можно им придать такое значение, чтобы их сумма была равна нулю, т.е. St=0. Отсчет времени ведется от середины ряда: • при нечетном числе уровней серединная точка принимается за ноль. Предшествующие периоды обозначаются -1, -2, -3 и т.д., следующие за центральным – соответственно 1. 2, 3 и т.д. • при четном числе уровней два серединных уровня обозначаются -1 и +1, а все последующие и предыдущие: ±3, ±5, ±7 и т.д. В этом случае система нормальных уравнений принимает вид
Syt = a1St2, расчет параметров упрощается: a0= Выравниванием рядов динамики пользуются для предсказания (прогноза) дальнейшего развития явления – экстраполяции, а также для нахождения недостающего члена ряда – интерполяции.
Чтобы решить вопрос, использование какой функции дает лучший результат, обычно сопоставляется сумма квадратов отклонений эмпирических уровней от теоретических, рассчитанных по разным функциям. Та функция, при которой эта сумма квадратов меньше, считается наиболее адекватной.
|
||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 831; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.135.89 (0.01 с.) |

 , но удобнее, если
, но удобнее, если  теоретическими
теоретическими  , которые рассчитаны по определенному уравнению
, которые рассчитаны по определенному уравнению 
 ,
, - случайная величина, отражающая колебания уровней вокруг тренда.
- случайная величина, отражающая колебания уровней вокруг тренда.













 , а вторые разности равны нулю
, а вторые разности равны нулю  , то для выравнивания ряда используется линейная функция
, то для выравнивания ряда используется линейная функция
 , а третьи разности приблизительно равны нулю
, а третьи разности приблизительно равны нулю  , то в качестве тренда выбирают параболу 2-го порядка
, то в качестве тренда выбирают параболу 2-го порядка

 , то применяют показательную функцию
, то применяют показательную функцию

 ,
,
 a0n + a1St = Sy,
a0n + a1St = Sy, ;
; 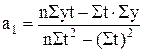 .
. Sy = a0n,
Sy = a0n, , a1=
, a1=  .
.



