
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средний уровень ряда динамики и приемы его вычисления.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Средний уровень ряда – это показатель, обобщающий итоги развития явления за единичный интервал или момент из имеющейся временной последовательности. Расчет среднего уровня ряда динамики определяется видом этого ряда и величиной интервала, соответствующего каждому уровню. Для интервальных рядов с равными периодами времени средний уровень Y рассчитывается следующим образом:
где n или (n +1) – общая длина временного ряда или общее число равных временных отрезков, каждому из которых соответствует свой уровень Yi (1 = 1, 2,..., n или 1 = 0, 1, 2,..., n). Средний абсолютный прирост рассчитывается по формулам в зависимости от способа нумерации интервалов (моментов).
Средний темп роста:
где Средний темп прироста (%) определяется по единственной методологии:
| ||
45 Преобразование рядов динамики: смыкание и приведение к одному основанию
При анализе рядов динамики приходится делать некоторые преобразования, которые улучшают условия анализа.
Приведение ряда динамики к одному основанию используется в случае, если необходимо сравнение или сопоставление тенденций в нескольких рядах.
Смыкание рядов динамики метод применяется, если необходимо совместить два динамических ряда, характеризующих одно явление. Понимают объединение в один ряд (более длинный) двух или нескольких рядов динамики уровни которых исчислены по разной методологии или разным территориальным границам.
47. Аналитическое выравнивание.
Аналитическое выравнивание. Под этим понимают определение основной проявляющейся во времени тенденции развития изучаемого явления. Развитие предстает перед исследователем как бы в зависимости только от течения времени. В итоге выравнивания временного ряда получают наиболее общий, суммарный, проявляющийся во времени результат действия всех причинных факторов. Отклонение конкретных уровней ряда от уровней, соответствующих общей тенденции, объясняют действием факторов, проявляющихся случайно или циклически. В результате приходят к трендовой модели
 где f(t)– уровень, определяемый тенденцией развития;
et – случайное и циклическое отклонение от тенденции.
Целью аналитического выравнивания динамического ряда является определение аналитической или графической зависимости f(t). На практике по имеющемуся временному ряду задают вид и находят параметры функции f(t), а затем анализируют поведение отклонений от тенденции. Функцию f(t) выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса.
Чаще всего при выравнивании используются следующие зависимости:
где f(t)– уровень, определяемый тенденцией развития;
et – случайное и циклическое отклонение от тенденции.
Целью аналитического выравнивания динамического ряда является определение аналитической или графической зависимости f(t). На практике по имеющемуся временному ряду задают вид и находят параметры функции f(t), а затем анализируют поведение отклонений от тенденции. Функцию f(t) выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса.
Чаще всего при выравнивании используются следующие зависимости:
 Линейная зависимость выбирается в тех случаях, когда в исходном временном ряду наблюдаются более или менее постоянные абсолютные цепные приросты, не проявляющие тенденции ни к увеличению, ни к снижению.
Параболическая зависимость используется, если абсолютные цепные приросты сами по себе обнаруживают некоторую тенденцию развития, но абсолютные цепные приросты абсолютных цепных приростов (разности второго порядка) никакой тенденции развития не проявляют.
Экспоненциальные зависимости применяются, если в исходном временном ряду наблюдается либо более или менее постоянный относительный рост (устойчивость цепных темпов роста, темпов прироста, коэффициентов роста), либо, при отсутствии такого постоянства, – устойчивость в изменении показателей относительного роста.
Оценка параметров (a0, a1, a2,...) осуществляется следующими методами: 1) методом избранных точек, 2) методом наименьших расстояний, 3) методом наименьших квадратов (МНК).
В большинстве расчетов используют метод наименьших квадратов, который обеспечивает наименьшую сумму квадратов отклонений фактических уровней от выравненных:
Линейная зависимость выбирается в тех случаях, когда в исходном временном ряду наблюдаются более или менее постоянные абсолютные цепные приросты, не проявляющие тенденции ни к увеличению, ни к снижению.
Параболическая зависимость используется, если абсолютные цепные приросты сами по себе обнаруживают некоторую тенденцию развития, но абсолютные цепные приросты абсолютных цепных приростов (разности второго порядка) никакой тенденции развития не проявляют.
Экспоненциальные зависимости применяются, если в исходном временном ряду наблюдается либо более или менее постоянный относительный рост (устойчивость цепных темпов роста, темпов прироста, коэффициентов роста), либо, при отсутствии такого постоянства, – устойчивость в изменении показателей относительного роста.
Оценка параметров (a0, a1, a2,...) осуществляется следующими методами: 1) методом избранных точек, 2) методом наименьших расстояний, 3) методом наименьших квадратов (МНК).
В большинстве расчетов используют метод наименьших квадратов, который обеспечивает наименьшую сумму квадратов отклонений фактических уровней от выравненных:
 Для линейной зависимости (f(t)=a0+a1t) параметр а0 обычно интерпретации не имеет, но иногда его рассматривают как обобщенный начальный уровень ряда; а1 – сила связи, т.е. параметр, показывающий, насколько изменится результат при изменении времени на единицу. Таким образом, а можно представить как постоянный теоретический абсолютный прирост. Построив уравнение регрессии, проводят оценку его надежности. Это делается посредством критерия Фишера (F). Фактический уровень (Fфакт) сравнивается с теоретическим (табличным) значением:
Для линейной зависимости (f(t)=a0+a1t) параметр а0 обычно интерпретации не имеет, но иногда его рассматривают как обобщенный начальный уровень ряда; а1 – сила связи, т.е. параметр, показывающий, насколько изменится результат при изменении времени на единицу. Таким образом, а можно представить как постоянный теоретический абсолютный прирост. Построив уравнение регрессии, проводят оценку его надежности. Это делается посредством критерия Фишера (F). Фактический уровень (Fфакт) сравнивается с теоретическим (табличным) значением:
 где k – число параметров функции, описывающей тенденцию; n – число уровней ряда;
где k – число параметров функции, описывающей тенденцию; n – число уровней ряда;
| 46 Понятие тенденции ряда. Сглаживание рядов с помощью скользящей средней.
Всякий ряд динамики теоретически может быть представлен в виде составляющих: 1) тренд – основная тенденция развития динамического ряда (к увеличению либо снижению его уровней); 2) циклические (периодические) колебания, в том числе сезонные; 3) случайные колебания.
Изучение тренда включает два основных этапа: 1) ряд динамики проверяется на наличие тренда; 2) производится выравнивание временного ряда и непосредственное выделение тренда с экстраполяцией полученных результатов.
Непосредственное выделение тренда может быть произведено:
Скользящая средняя. В этом методе исходные уровни ряда заменяются средними величинами, которые получают из данного уровня и нескольких симметрично его окружающих. Целое число уровней, по которым рассчитывается среднее значение, называют интервалом сглаживания. Интервал может быть нечетным (3, 5, 7 и т.д. точек) или четным (2, 4, 6 и т.д. точек).
При нечетном сглаживании полученное среднее арифметическое значение закрепляют за серединой расчетного интервала, при четном этого делать нельзя. Поэтому при обработке ряда четными интервалами их искусственно делают нечетными, для чего образуют ближайший больший нечетный интервал, но из крайних его уровней берут только 50 %.
Недостаток методики сглаживания скользящими средними состоит в условности определения сглаженных уровней для точек в начале и конце ряда. Получают их специальными приемами – расчетом средней арифметической взвешенной.
48 Сезонные колебания и методы их изучения
Сезонные колебания – это сравнительно устойчивые внутригодичные колебания явления. Они вызываются рядом объективных причин (природно-климатическими) и ведут к ухудшению показателей работы предприятий. Анализ сезонных колебаний необходим для улучшения оперативного планирования и разработки мероприятий для уменьшения их отрицательных воздействий.
Для измерения сезонных колебаний предложены следующие методы:
метод абсолютных разностей; метод относительных разностей; построение индексов сезонности.
При использовании метода абсолютных разностей вначале определяют средний уровень явления за каждый месяц по 3-х летним данным, затем определяют среднюю за весь рассматриваемый период.
Далее определяется абсолютное отклонение средних за каждый месяц от общей средней.
Метод относительных разностей является развитием метода абсолютных разностей. Для нахождения относительных разностей абсолютные отклонения делят на общую среднюю и выражают в процентах.
Глубину сезонных колебаний измеряют индексами сезонности (Iсез):
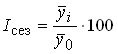 ,
где ,
где  – средняя из фактических средних уровней одноименных месяцев; – средняя из фактических средних уровней одноименных месяцев;
 – общая средняя за исследуемый период.
Индекс сезонности показывает, на сколько среднемесячное потребление каждого месяца отличается от общего среднего за весь период.
49. Понятие интерполяции и экстраполяции.
Выравниванием рядов динамики пользуются для того, чтобы найти значение недостающего члена ряда. Такой способ называется интерполяцией. Экстраполяцией рядов динамики называют прием, который заключается в том, что, продолжая найденные математические кривые можно предсказать дальнейшее развитие событий. Прогнозирование базируется на знании развития прогнозируемого явления, а также факторов, влияющих на это явление и того, каким образом эти факторы могут изменить развитие явления
Интерполяция – приближенный расчет уровней, лежащих внутри ряда динамики, но почему-то неизвестных. Простейшим способом интерполяции является интерполяция методом ближайшего соседа (при котором в качестве промежуточного значения выбирается ближайшее известное значение функции). – общая средняя за исследуемый период.
Индекс сезонности показывает, на сколько среднемесячное потребление каждого месяца отличается от общего среднего за весь период.
49. Понятие интерполяции и экстраполяции.
Выравниванием рядов динамики пользуются для того, чтобы найти значение недостающего члена ряда. Такой способ называется интерполяцией. Экстраполяцией рядов динамики называют прием, который заключается в том, что, продолжая найденные математические кривые можно предсказать дальнейшее развитие событий. Прогнозирование базируется на знании развития прогнозируемого явления, а также факторов, влияющих на это явление и того, каким образом эти факторы могут изменить развитие явления
Интерполяция – приближенный расчет уровней, лежащих внутри ряда динамики, но почему-то неизвестных. Простейшим способом интерполяции является интерполяция методом ближайшего соседа (при котором в качестве промежуточного значения выбирается ближайшее известное значение функции).
| ||
50. Статистические методы прогнозирования на основе рядов динамики.
Под прогнозом понимается научно обоснованное описание возможных состояний объектов в будущем, а также альтернативных путей и сроков достижения этого состояния. Сам процесс разработки прогнозов называется прогнозированием. Прогнозирование - это вид познавательной деятельности человека, направленной на формирование прогнозов развития объекта на основе анализа тенденций его развития. Методами прогнозирования называются совокупность приемов мышления, позволяющих на основе анализа прошлых (ретроспективных) внешних и внутренних связей, присущих объекту, а так же их изменений в рамках рассматриваемого явления вынести суждение определенной достоверности относительно будущего развития объекта. Выбор методов прогнозирования осуществляется в соответствии с характером объекта и требований, предъявляемых к информационному обеспечению. Наиболее сложным методом прогнозирования является прогнозирование на основевзаимосвязанных рядов динамики. С его помощью можно получить не только оценки результативного, но и факторных признаков, т.е. анализ взаимосвязанных рядов динамики выражается с помощью системы уравнений регрессии. Прогноз в этом случае лучше поддается содержательной интерпретации, чем простая экстраполяция. 52. Понятие об идексах. Индексы индивидуальные и общие.
Индекс – это обобщающий показатель сравнения экономических явлений, состоящих из элементов, не поддающихся суммированию. Для того чтобы проанализировать подобного рода элементы, необходимо найти общую единицу измерения этих элементов. Индексный метод наиболее широко применяется для анализа экономических явлений и для исчисления темпов динамики. Он так же может быть использован для сравнения показателей, как однородных, так и разнородных, либо за один период времени, так и за несколько периодов. Он дает возможность выявить роль каждого фактора в изменении средней.
Индивидуальные индексы дают характеристику изменения отдельных элементов сложного явления. Общие индексы дают характеристику сложных явлений в целом. Часто исчисляют не общий индекс, а субиндекс, т.е. не все элементы явления, а только часть. Из всех этих индексов, групповые индексы имеют большее экономическое значение, потому что они раскрывают закономерности в развитии всего явления. В статистике групповые индексы применяются в целом по промышленности, по народному хозяйству, а так же по отдельным группам товаров.
Любой индекс получается в результате сравнения двух абсолютных уровней изучаемого явления. Но исчисляются так же и динамические индексы, когда берут уровни различных периодов. Тот уровень, который сравнивается, называется отчетным или текущим; а тот период, с уровнем которого сравнивается – базисным.
Т.о. каждый индекс каждый индекс характеризует уровень изучаемого явления в отчетном периоде по сравнению с базисным. И, если этот уровень в отчетном периоде больше, чем в базисном, то индекс больше единицы. В первом случае разность между индексом, выраженном в процентах, показывает, на сколько процентов уровень базисного периода выше или ниже отчетного, а во втором случае, – на сколько процентов уровень отчетного периода меньше базисного.
53. Объективность общим индексам придает их запись в агрегатном виде, предложенная испанцем Ласпейресом и немцем Пааше.
Агрегатный общий индекс Ласпейреса для количества товаров как первого фактора выручки определяется по формуле
 = =  (1.75)
Аналогично можно записать агрегатный общий индекс Ласпейреса для цен как первого фактора выручки, то есть (1.75)
Аналогично можно записать агрегатный общий индекс Ласпейреса для цен как первого фактора выручки, то есть
 = =  (1.76)
В формулах Ласпейреса знаменатели по существу одинаковые, представляя собой выручку базисного периода, а числители разные. В формуле (1.75) это отчетная выручка в базисных ценах (количесгво товаров отчетное, а цены — базисные), в формуле (1.76) наоборот — базисная выручка в отчетных ценах (цены отчетные, а количество товаров — базисное).
Агрегатные общие индексы Пааше применяются ко вторым факторам мультипликативных моделей. Поэтому такой индекс для цен как второго фактора выручки определяется по формуле (1.76)
В формулах Ласпейреса знаменатели по существу одинаковые, представляя собой выручку базисного периода, а числители разные. В формуле (1.75) это отчетная выручка в базисных ценах (количесгво товаров отчетное, а цены — базисные), в формуле (1.76) наоборот — базисная выручка в отчетных ценах (цены отчетные, а количество товаров — базисное).
Агрегатные общие индексы Пааше применяются ко вторым факторам мультипликативных моделей. Поэтому такой индекс для цен как второго фактора выручки определяется по формуле
 = = 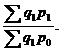 (1.77)
Аналогично можно записать агрегатный общий индекс Пааше для количества товаров как второго фактора выручки, то есть (1.77)
Аналогично можно записать агрегатный общий индекс Пааше для количества товаров как второго фактора выручки, то есть
 = = 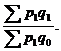 (1.78)
В формулах Пааше числители по существу одинаковые, представляя собой выручку отчетного периода, а знаменатели аналогичны числителям формул Ласпейреса.
Для облегчения запоминания студентами формул Ласпейреса и Пааше предлагаю обратить внимание на букву «ш» в слове «Пааше», которая напоминает «111» - так обозначены отчетные периоды в общей формуле (две единицы – в числителе, а одна – в знаменателе). В формуле же Ласпейреса – три нуля (наоборот к формуле Пааше).
Произведения количественного индекса Ласпейреса и ценового индекса Пааше, а также ценового индекса Ласпейреса и количественного индекса Пааше дают общий индекс выручки.
Однако вид этих формул показывает, что однофакторные индексы Ласпейреса и Пааше не равны между собой. То есть не равными являются количественные индексы Ласпейреса и Пааше и ценовые. Американский экономист Гершенкрон обширными расчетами установил, что по одному и тому же фактору индекс Ласпейреса всегда больше индекса Пааше и это открытие названо эффектом Гершенкрона.
Но в статистике должно быть одно значение индекса, поэтому американский экономист Фишер предложил применять среднюю геометрическую величину из индексов Ласпейреса и Пааше, определяя ее по формулам:
для количества товаров (1.78)
В формулах Пааше числители по существу одинаковые, представляя собой выручку отчетного периода, а знаменатели аналогичны числителям формул Ласпейреса.
Для облегчения запоминания студентами формул Ласпейреса и Пааше предлагаю обратить внимание на букву «ш» в слове «Пааше», которая напоминает «111» - так обозначены отчетные периоды в общей формуле (две единицы – в числителе, а одна – в знаменателе). В формуле же Ласпейреса – три нуля (наоборот к формуле Пааше).
Произведения количественного индекса Ласпейреса и ценового индекса Пааше, а также ценового индекса Ласпейреса и количественного индекса Пааше дают общий индекс выручки.
Однако вид этих формул показывает, что однофакторные индексы Ласпейреса и Пааше не равны между собой. То есть не равными являются количественные индексы Ласпейреса и Пааше и ценовые. Американский экономист Гершенкрон обширными расчетами установил, что по одному и тому же фактору индекс Ласпейреса всегда больше индекса Пааше и это открытие названо эффектом Гершенкрона.
Но в статистике должно быть одно значение индекса, поэтому американский экономист Фишер предложил применять среднюю геометрическую величину из индексов Ласпейреса и Пааше, определяя ее по формулам:
для количества товаров  = =  (1.79)
для цен (1.79)
для цен  = =  (1.80)
Вместе с тем, проведенные Ворониным В.Ф. многочисленные расчеты показали, что для целей статистики вполне можно применять не среднюю геометрическую, а простую среднюю арифметическую величину из индексов Ласпейреса и Пааше, определяя ее по формулам:
для количества товаров (1.80)
Вместе с тем, проведенные Ворониным В.Ф. многочисленные расчеты показали, что для целей статистики вполне можно применять не среднюю геометрическую, а простую среднюю арифметическую величину из индексов Ласпейреса и Пааше, определяя ее по формулам:
для количества товаров  = =  (1.81)
для цен (1.81)
для цен  = =  (1.82)
Например, если индекс Ласпейреса 1,8 и индекс Пааше 1,4, то средний геометрический индекс по предложению Фишера равняется
IФ= (1.82)
Например, если индекс Ласпейреса 1,8 и индекс Пааше 1,4, то средний геометрический индекс по предложению Фишера равняется
IФ=  =1,59,
а средний арифметический индекс по нашему предложению составит
IВ=(1,8+1,4)/2 = 1,60.
Как видим, разница очень незначительная. Но при этом важно во всехпериодах времени постоянно пользоваться одной и той же средней величиной: или геометрической, или арифметической. =1,59,
а средний арифметический индекс по нашему предложению составит
IВ=(1,8+1,4)/2 = 1,60.
Как видим, разница очень незначительная. Но при этом важно во всехпериодах времени постоянно пользоваться одной и той же средней величиной: или геометрической, или арифметической.
| 51. При изучении развития явления во времени часто возникает необходимость оценить степень взаимосвязи в изменениях уровней 2-х или более рядов динамики различного содержания, но связанных между собой. Эта задача решается методами коррелирования:
· уровней ряда динамики
· отклонений фактических уровней от тренда
· последовательных разностей
Коррелирование уровней динамических рядов с применением парного коэффициента корреляции правильно показывает тесноту связи лишь в том случае, если в каждом из них отсутствует автокорреляция. Наличие зависимости между последующими и предшествующими уровнями динамического ряда в статистической литературе называютавтокорреляцией.
Поэтому прежде, чем коррелировать ряды динамики по уровням, необходимо проверить каждый из рядов на наличие или отсутствие в них автокорреляции. Применение методов классической теории корреляции в динамических рядах связано с некоторыми особенностями. Прежде всего, это наличие для большинства динамических рядов зависимости последующих уровнейотпредыдущих.
Коэффициент автокорреляции вычисляется по непосредственным данным рядов динамики, когда фактические уровни одного ряда рассматриваются как значенияфакторного признака, а уровни этого же ряда со сдвигом на один период, принимаются в качестве результативного признака (этот сдвиг называется лагом). Коэффициент автокорреляции рассчитывается на основе формулы коэффициента корреляции для парной зависимости:
где:
· yt – фактические уровни ряда,
· yt+1– уровни того же ряда со сдвигом на 1 период (коэффициент автокорреляции первого порядка).
Примечание: во избежание путаницы, следует обратить внимание на порядок, по которому будет производиться сдвиг уровней, а именно, вниз или вверх. Соответственно и в формулахпо разным источникам, ряд со сдвигом отображают либо так yt-1 либо yt+1
Формула для расчета коэффициента автокорреляции уровней ряда 1-го порядка:
 Формула для расчета коэффициента автокорреляции уровней ряда 2-го порядка:
Формула для расчета коэффициента автокорреляции уровней ряда 2-го порядка:
 Для суждения о наличии или отсутствии автокорреляции в исследуемом ряду, фактическое значение коэффициента автокорреляции сопоставляют с табличным для 5% или 1% уровня значимости (т. е. по величине вероятности допустить ошибку при принятии гипотезы о независимости уровней ряда). Если расчетное значение меньше табличного, то гипотеза об отсутствии автокорреляции принимается и, наоборот, в противном случае, отвергается.
Последовательность коэффициентов автокорреляции 1, 2 и т.д. порядков называютавтокорреляционной функциейвременного ряда. График зависимости значений коэффициентов автокорреляции от величины лага (порядка коэффициента автокорреляции) называют коррелограммой.
Анализ автокорреляционной функции и коррелограммы позволяет выявить структуру ряда, т. е. определить присутствие в ряде той или иной компоненты. Так, если наиболее высоким оказался коэффициент автокорреляции первого порядка, то исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка m, то ряд содержит циклические колебания с периодичностью в m моментов времени. Если же ни один из коэффициентов автокорреляции не является значимым, то можно сделать одно из двух предположений:
· либо ряд не содержит тенденции и циклических колебаний, а его уровень определяется только случайной компонентой;
· либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ.
Необходимо подчеркнуть, что линейные коэффициенты автокорреляции характеризуют тесноту только линейной связи текущего и предыдущих уровней ряда. Поэтому, по коэффициентам автокорреляции можно судить только о наличии или отсутствии линейной зависимости(или близкой к линейной). Для некоторых временных рядов, имеющихсильную нелинейную тенденцию (например, параболу второго порядка или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к нулю. По знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Большинство временных рядов экономических данных содержат положительную автокорреляцию уровней, однако, при этом могут иметь убывающую тенденцию.
Для проверки ряда на наличие нелинейной тенденции рекомендуется вычислить линейные коэффициенты автокорреляции для временного ряда, состоящего из логарифмов исходных уровней. Отличные от нуля значения коэффициентов автокорреляции будут свидетельствовать о наличии нелинейной тенденции.
Для суждения о наличии или отсутствии автокорреляции в исследуемом ряду, фактическое значение коэффициента автокорреляции сопоставляют с табличным для 5% или 1% уровня значимости (т. е. по величине вероятности допустить ошибку при принятии гипотезы о независимости уровней ряда). Если расчетное значение меньше табличного, то гипотеза об отсутствии автокорреляции принимается и, наоборот, в противном случае, отвергается.
Последовательность коэффициентов автокорреляции 1, 2 и т.д. порядков называютавтокорреляционной функциейвременного ряда. График зависимости значений коэффициентов автокорреляции от величины лага (порядка коэффициента автокорреляции) называют коррелограммой.
Анализ автокорреляционной функции и коррелограммы позволяет выявить структуру ряда, т. е. определить присутствие в ряде той или иной компоненты. Так, если наиболее высоким оказался коэффициент автокорреляции первого порядка, то исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка m, то ряд содержит циклические колебания с периодичностью в m моментов времени. Если же ни один из коэффициентов автокорреляции не является значимым, то можно сделать одно из двух предположений:
· либо ряд не содержит тенденции и циклических колебаний, а его уровень определяется только случайной компонентой;
· либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ.
Необходимо подчеркнуть, что линейные коэффициенты автокорреляции характеризуют тесноту только линейной связи текущего и предыдущих уровней ряда. Поэтому, по коэффициентам автокорреляции можно судить только о наличии или отсутствии линейной зависимости(или близкой к линейной). Для некоторых временных рядов, имеющихсильную нелинейную тенденцию (например, параболу второго порядка или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к нулю. По знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Большинство временных рядов экономических данных содержат положительную автокорреляцию уровней, однако, при этом могут иметь убывающую тенденцию.
Для проверки ряда на наличие нелинейной тенденции рекомендуется вычислить линейные коэффициенты автокорреляции для временного ряда, состоящего из логарифмов исходных уровней. Отличные от нуля значения коэффициентов автокорреляции будут свидетельствовать о наличии нелинейной тенденции.
| ||
№54. Агрегатный индекс как основная форма сводных индексов. Проблема выбора весов или соизмерителей.
Агрегатным является индекс, представляющий собой отношение двух абсолютных сумм затрат на производство продукции, исчисленных, при одинаковом количестве продукции отчетного периода.
, где
- цены базисного периода,
- цены отчетного периода,
- количество товаров в натуральном выражении отчетного периода.
Для исчисления общего признака нужно, прежде всего, перейти от совокупности элементов, непосредственно не поддающихся суммированию, к другим совокупностям, элементы которых можно складывать. И этот переход производится с помощью соизмерителей (весов), вводимых в индекс. Такие соизмерители индекса определяют на основе экономического анализа сущности изучаемого явления. Система взаимосвязанных индексов.
Индексный метод широко используется при анализе экономических ситуаций, особенно, когда процесс динамичен, но всегда в результате требуется проанализировать не заключительные данные, а промежуточные результаты, которые во многом зависят от ряда факторов. Поэтому в данном явлении отдельные индексы связаны между собой индексами количества и цены.
56) При изучении динамики явления за ряд последовательных периодов (лет, месяцев), рассчитывают ряд индексов. Эти индексы показывают изменение явления либо по отношению к постоянной базе (базисные индексы), либо по отношению к переменной базе (цепные индексы). Цепныеибазисные индексымогут бытьиндивидуальнымииобщими. Расчет индивидуальных индексов при этом прост — для удобства записи отсчет времени начинают с первого периода.
Сумма произведений индивидуальных цепных индексов дает базисный индекс за соответствующий период.
Индексные величины могут определяться как на постоянной, так и на переменной базах сравнения. При этом, если задача анализа состоит в получении характеристик изменения изучаемого явления во всех последующих периодах по сравнению с начальным, то вычисляютсябазисные индексы. Например, сопоставление объёма розничного товарооборота II, III и IV кварталов с I кварталом.
Но если требуется охарактеризовать последовательные изменения изучаемого явления из периода в период, то вычисляются цепные индексы. Например, при изучении объёма розничного товарооборота по кварталам года сопоставляют товарооборот II квартала c I, III — cо II и IV — с III кварталом.
Частное от деления последующего базисного индекса на предыдущий индекс дает нам цепной индекс за соответствующий период.
Преимущество сводных индексов с постоянными весами состоит в том, что их можно сравнивать между собой, а также получать цепные индексы из базисных и наоборот.
Для индексов с переменными весами такое правило не сохраняется.
В зависимости от задачи исследования и характера исходной информации базисные и цепные индексы исчисляются как индивидуальные, так и общие.
Способы расчёта индивидуальных базисных и цепных индексов аналогичны расчёту относительных величин динамики. Общие индексы в зависимости от их вида вычисляются с переменными и постоянными весами — соизмерителями.
Используя индексный ряд за несколько периодов, можно получить динамику стоимости продукции и динамику товарооборота в неизменных ценах, т. е. в ценах какого — то одного прошлого периода. Такие индексные ряды называются индексами с постоянными весами. Для них действует правило:произведение цепных индексов даст индекс базисный.
С постоянными весами рассчитываются индексы физического объема продукции, а с переменными весами – индексы цен, себестоимости, производительности труда.
При построении базисных и цепных общих индексов возникает проблема весов. Веса при этом могут быть постоянными (т.е. одинаковыми во всех индексах) и могут бытьпеременными (т. е. изменяющимися от индекса к индексу).
В большинстве случаев принято все индексы (базисные и цепные) количественных показателей записывать с постоянными весами.
Многие экономические индексы тесно связаны между собой и образуют индексные системы. Так, индекс цен связан с индексом физического объема товарооборота или физического объема продукции,образуя следующую индексную систему:
 Произведение индекса цен на индекс физического объема товарооборота или продукции дает индекс физического объема товарооборота в фактических ценах, или индекс стоимости продукции.
Индекс себестоимости промышленной продукции связан с индексом физического объема продукции по себестоимости.
Произведениеиндекса себестоимости продукции на индекс физического объемадаетиндекс затрат в производстве:
Произведение индекса цен на индекс физического объема товарооборота или продукции дает индекс физического объема товарооборота в фактических ценах, или индекс стоимости продукции.
Индекс себестоимости промышленной продукции связан с индексом физического объема продукции по себестоимости.
Произведениеиндекса себестоимости продукции на индекс физического объемадаетиндекс затрат в производстве:
 Используя индексные системы, можно по двум известным индексам найти третий, неизвестный.
Индексы постоянного состава, переменного состава и структурных сдвигов
В тех случаях, когда анализируется изменение во времени сравниваемой продукции, можно поставить вопрос о том, как в различных условиях (на различных участках) меняются составляющие индекса (цена, физический объем, структура производства или реализация отдельных видов продукции). В связи с этим строятся индексы постоянного состава,переменного состава, структурных сдвигов.
Индекс постоянного (фиксированного) состава по своей форме тождественен агрегатному индексу.
Индекс переменного состава используется для характеристики изменения средней цены в текущем и базисном периодах.
Индекс-дефлятор используется для перевода значений стоимостных показателей за отчетный период в стоимостные измерители базисного периода. Для построения индекса дефлятора можно использовать индексы с переменными весами.
Базисные и цепные индексы. Два варианта сводных цепных индексов
В зависимости от базы сравнения индексы бывают базисными и цепными.
В системе базисных индексов сравнения уровней индексируемого показателя в каждом индексе производится с уровнем базисного периода, а в системе цепных индексов уровни индексируемого показателя сопоставляются с уровнем предыдущего периода.
Цепные и базисные индексы могут быть как индивидуальные, так и общие.
Ряды индивидуальных индексов просты по построению. Так, например, обозначив четыре последовательных периода подстрочными значениями 0, 1,2, 3, исчисляем базисные и цепные индивидуальные индексы цен:
· базисные индексы
· цепные индексы
Любой агрегатный индекс может быть представлен как взвешенная величина из индивидуальных индексов
найдем
Подставим в общий индекс цены
тогда получим среднегармонический взвешенный индекс
отсюда q1 = iq?q0, подставим в агрегатную форму общего индекса физического объема
Получили средневзвешенный индекс. Вот для каких целей используется индивидуальный индекс, т.е. расширяет возможности агрегатной формы индекса.
Использование исходной формы агрегатного индекса или среднегармонического, средневзвешенного индекса зависит от исходных данных, имеющихся в распоряжении исследователя.
№61
Статистика населения и трудовых ресурсов В силу разноплановости трудовых ресурсов состав работников на предприятии изучается в следующих направлениях [1]: 1) по отраслевой принадлежности; 2) по участкам работы; 3) по функциям, выполняемым в процессе производства. В зависимости от отраслевой принадлежности подразделения предприятий выделяют персонал основной деятельности или промышленно-производственный персонал и персонал непромышленных организаций. По выполняемым функциям работники промышленно-производственного персонала подразделяются на шесть категорий: рабочие, ученики, инженерно-технические работники (ИТР), служащие, младший обслуживающий персонал (МОП) и работники охраны. Самой многочисленной и основной частью состава работников являются рабочие. К рабочим относятся лица, непосредственно связанные с производством продукции, а также лица, занятые ремонтом и уходом за оборудованием, доставкой материала к рабочим местам и т.д. К ученикам относятся лица, обучающиеся на производстве той или иной профессии рабочих и получающие заработную плату. ИТР составляют ту часть предприятия, которые осуществляют организацию и руководство производственным и технологическим процессом. К служащим относятся работники, выполняющие административно-управленческие и хозяйственные функции. К МОПу относят работников, имеющих дело с обслуживанием производственных и непроизводственных помещений. В зависимости от роли в процессе производства продукции различают основных и вспомогательных рабочих. К основным относят рабочих, непосредственно занятые изготовлением продукции, приводящие к действию производственное оборудование. К вспомогательным относятся рабочие, занятые обслуживанием основных рабочих, оборудования, на автоматизации их труда. Рабочие основные и вспомогательные в свою очередь характеризуются степенью механизации и автоматизации их труда. Важнейшим статистическим показателем численности работников предприятия является величина среднего списочного числа работников. Средняя списочная численность работников предприятия или цеха, принятых за неполный рабочий день, исчисляется так: общее число человеко-часов, отработанных этими работниками за месяц, делится на установленную продолжительность рабочего дня и полученное таким образом число отработанных человеко-дней, делят на число рабочих дней в месяце по календарю [1]. Например, за месяц, в котором по календарю 22 рабочих дня, рабочими отработано 12500 человеко-часов. Тогда при пятидневной рабочей недели число отработанных человеко-дней составит 1524, как частное от деления 12500 на 8,2; т.е.12500:8,2. Средняя списочная численность рабочих, принятых за неполный рабочий день (1524:22=69 чел.) составит 69 человек. Таким образом, среднюю списочную численность работников, принятых за неполную рабочую неделю, определяют как отношение отработанных этими Работниками человеко-дней к числу рабочих дней в отведённом месяце по календарю. А среднее списочное число работников работающих полный рабочий день вычисляется как среднюю арифметическую простую в течение определённого отрезка времени (месяц, квартал, год). Предположим, что за первое полугодие средняя списочная численность промышленно-производственного персонала составила 730 человек, а за июль — 710, август 700. Средняя списочная численность промышленно-производственного персонала за январь — август (8 мес.) будет равняться: (736х6+710х1+700х1):8=5826:8=728 Основное внимание экономическая статистика уделяет той части трудовых ресурсов, которая принимает участие в общественном труде. Не менее важной задачей остаётся определение занятых работников по отрасли народного хозяйства. Выделяются две группы трудовых ресурсов: занятые физическим трудом и занятые умственным трудом. Трудовые ресурсы — это часть населения страны, которая по возрас ту и состоянию здоровья способна к трудовой деятельности. В состав трудовых ресурсов включают: • трудоспособное население в трудоспособном возрасте; • фактически работающих подростков моложе 16 лет; • фактически работающих лиц старше трудоспособного возраста. Изменение численности трудовых ресурсов (пополнение, выбытие и естественный прирост), не связанных с миграцией населения, назы ваетсяестественнымдвижением трудовых ресурсов. Естественное пополнение трудовых ресурсов(ПТРестеств.) происходит за счет вступления в трудоспособный возраст подростков, а также за счет привлечения к трудовой деятельности пенсионеров и лиц моложе 16 лет. Естественное выбытие трудовых ресурсов(ВТРестеств.) происходит за счет смертности, перехода на пенсию или инвалидность. Естественный прирост трудовых ресурсов — это разность между ес тественным пополнением и естественным выбытием трудовых ресур сов. Подмеханическимдвижением трудовых ресурсов понимается из менение их численности за счет миграции. Для характеристики изменения численности трудовых ресурсов используются следующие относительные показатели: • коэффициент естественного пополнения трудовых ресурсов: % • коэффициент естественного выбытия трудовых ресурсов: % • коэффициент естественного прироста трудовых ресурсов: • коэффициент миграционного прироста: % Население, активное в данный период (или рабочая сила), — наи более часто используемый показатель, характеризующий численность экономически активного населения. Коэффициент экономической ак тивности населенияопределяется по формуле:, где — численность экономически активного населения на дату — t; — численность всего населения на ту же дату. На основе данных о численности занятого населения и экономи чески активного населения рассчитывается коэффициент занятости населения: где — численность занятых на дату. Коэффициент занятости рассчитывается как по населению в це лом, так и по полу и отдельным возрастным группам. К безработнымотносятся лицаот16 лет и старше, которые в тече ние рассматриваемого периода [1]: • не имели работы либо занятия, приносящего доход; • искали работу; • готовы были приступить к работе. При отнесении того или иного лица к категории безработных долж ны учитываться все три указанных критерия. Для характеристики уровня безработицы исчисляется коэффици ент безработицы: где — численность безработных на дату; Р — численность экономически активного населения на дату. Данные о безработице разрабатываются по полу, возрасту и семей ному положению. Изучается также распределение безработных по об разованию и профессиональной принадлежности. Списочная численность работников-это сумма работников, явив шихся и не явившихся по различным причинам. Явившиеся работники подразделяются на фактически работавших, т. е. приступивших к работе независимо от продолжительности рабочего дня, и не приступивших к работе независимо от причин, т. е. имевших целодневные простои. Не явившиеся (временно отсутствующие) работники подразделяют ся на основании причины неявок. Среднесписочная численность работниковза период определяется отношением [2]: где — сумма списочных чисел за период/число календарных дней в периоде. Средняя списочная численность работников за год находится по средней из средних списочных чисел за все месяцы. При этом, если предприятие работало неполный год, то сумма средних списочных численностей все равно делится на 12 месяцев.
№66
Национальное богатство представляет собой совокупность материальных благ, созданных трудом предшествующих и нынешнего поколений, а также природных ресурсов, разведанных и вовлеченных в экономический оборот, нематериальных активов и ценностей.
Категория «национальное богатство» используется для оценки экономического потенциала и уровня экономического развития страны, а также для международных сопоставлений. Система показателей статистики национального богатства включает в себя следующие основные характеристики:
1) наличия (объема) и структуры богатства;
2) воспроизводства важнейших его частей;
3) динамики всего богатства и его составных частей;
4) размещения богатства на территории страны;
5) охраны природных ресурсов и их восполнения.
Объем национального богатства исчисляется, как правило, в стоимостном выражении в текущих и сопоставимых ценах на определенный период времени (обычно на начало и конец года). Объем НБ в текущих ценах отражает стоимость его элементов в ценах приобретения соответствующих периодов. В сопоставимых ценах НБ отражает стоимость всех его элементов в це
Используя индексные системы, можно по двум известным индексам найти третий, неизвестный.
Индексы постоянного состава, переменного состава и структурных сдвигов
В тех случаях, когда анализируется изменение во времени сравниваемой продукции, можно поставить вопрос о том, как в различных условиях (на различных участках) меняются составляющие индекса (цена, физический объем, структура производства или реализация отдельных видов продукции). В связи с этим строятся индексы постоянного состава,переменного состава, структурных сдвигов.
Индекс постоянного (фиксированного) состава по своей форме тождественен агрегатному индексу.
Индекс переменного состава используется для характеристики изменения средней цены в текущем и базисном периодах.
Индекс-дефлятор используется для перевода значений стоимостных показателей за отчетный период в стоимостные измерители базисного периода. Для построения индекса дефлятора можно использовать индексы с переменными весами.
Базисные и цепные индексы. Два варианта сводных цепных индексов
В зависимости от базы сравнения индексы бывают базисными и цепными.
В системе базисных индексов сравнения уровней индексируемого показателя в каждом индексе производится с уровнем базисного периода, а в системе цепных индексов уровни индексируемого показателя сопоставляются с уровнем предыдущего периода.
Цепные и базисные индексы могут быть как индивидуальные, так и общие.
Ряды индивидуальных индексов просты по построению. Так, например, обозначив четыре последовательных периода подстрочными значениями 0, 1,2, 3, исчисляем базисные и цепные индивидуальные индексы цен:
· базисные индексы
· цепные индексы
Любой агрегатный индекс может быть представлен как взвешенная величина из индивидуальных индексов
найдем
Подставим в общий индекс цены
тогда получим среднегармонический взвешенный индекс
отсюда q1 = iq?q0, подставим в агрегатную форму общего индекса физического объема
Получили средневзвешенный индекс. Вот для каких целей используется индивидуальный индекс, т.е. расширяет возможности агрегатной формы индекса.
Использование исходной формы агрегатного индекса или среднегармонического, средневзвешенного индекса зависит от исходных данных, имеющихся в распоряжении исследователя.
№61
Статистика населения и трудовых ресурсов В силу разноплановости трудовых ресурсов состав работников на предприятии изучается в следующих направлениях [1]: 1) по отраслевой принадлежности; 2) по участкам работы; 3) по функциям, выполняемым в процессе производства. В зависимости от отраслевой принадлежности подразделения предприятий выделяют персонал основной деятельности или промышленно-производственный персонал и персонал непромышленных организаций. По выполняемым функциям работники промышленно-производственного персонала подразделяются на шесть категорий: рабочие, ученики, инженерно-технические работники (ИТР), служащие, младший обслуживающий персонал (МОП) и работники охраны. Самой многочисленной и основной частью состава работников являются рабочие. К рабочим относятся лица, непосредственно связанные с производством продукции, а также лица, занятые ремонтом и уходом за оборудованием, доставкой материала к рабочим местам и т.д. К ученикам относятся лица, обучающиеся на производстве той или иной профессии рабочих и получающие заработную плату. ИТР составляют ту часть предприятия, которые осуществляют организацию и руководство производственным и технологическим процессом. К служащим относятся работники, выполняющие административно-управленческие и хозяйственные функции. К МОПу относят работников, имеющих дело с обслуживанием производственных и непроизводственных помещений. В зависимости от роли в процессе производства продукции различают основных и вспомогательных рабочих. К основным относят рабочих, непосредственно занятые изготовлением продукции, приводящие к действию производственное оборудование. К вспомогательным относятся рабочие, занятые обслуживанием основных рабочих, оборудования, на автоматизации их труда. Рабочие основные и вспомогательные в свою очередь характеризуются степенью механизации и автоматизации их труда. Важнейшим статистическим показателем численности работников предприятия является величина среднего списочного числа работников. Средняя списочная численность работников предприятия или цеха, принятых за неполный рабочий день, исчисляется так: общее число человеко-часов, отработанных этими работниками за месяц, делится на установленную продолжительность рабочего дня и полученное таким образом число отработанных человеко-дней, делят на число рабочих дней в месяце по календарю [1]. Например, за месяц, в котором по календарю 22 рабочих дня, рабочими отработано 12500 человеко-часов. Тогда при пятидневной рабочей недели число отработанных человеко-дней составит 1524, как частное от деления 12500 на 8,2; т.е.12500:8,2. Средняя списочная численность рабочих, принятых за неполный рабочий день (1524:22=69 чел.) составит 69 человек. Таким образом, среднюю списочную численность работников, принятых за неполную рабочую неделю, определяют как отношение отработанных этими Работниками человеко-дней к числу рабочих дней в отведённом месяце по календарю. А среднее списочное число работников работающих полный рабочий день вычисляется как среднюю арифметическую простую в течение определённого отрезка времени (месяц, квартал, год). Предположим, что за первое полугодие средняя списочная численность промышленно-производственного персонала составила 730 человек, а за июль — 710, август 700. Средняя списочная численность промышленно-производственного персонала за январь — август (8 мес.) будет равняться: (736х6+710х1+700х1):8=5826:8=728 Основное внимание экономическая статистика уделяет той части трудовых ресурсов, которая принимает участие в общественном труде. Не менее важной задачей остаётся определение занятых работников по отрасли народного хозяйства. Выделяются две группы трудовых ресурсов: занятые физическим трудом и занятые умственным трудом. Трудовые ресурсы — это часть населения страны, которая по возрас ту и состоянию здоровья способна к трудовой деятельности. В состав трудовых ресурсов включают: • трудоспособное население в трудоспособном возрасте; • фактически работающих подростков моложе 16 лет; • фактически работающих лиц старше трудоспособного возраста. Изменение численности трудовых ресурсов (пополнение, выбытие и естественный прирост), не связанных с миграцией населения, назы ваетсяестественнымдвижением трудовых ресурсов. Естественное пополнение трудовых ресурсов(ПТРестеств.) происходит за счет вступления в трудоспособный возраст подростков, а также за счет привлечения к трудовой деятельности пенсионеров и лиц моложе 16 лет. Естественное выбытие трудовых ресурсов(ВТРестеств.) происходит за счет смертности, перехода на пенсию или инвалидность. Естественный прирост трудовых ресурсов — это разность между ес тественным пополнением и естественным выбытием трудовых ресур сов. Подмеханическимдвижением трудовых ресурсов понимается из менение их численности за счет миграции. Для характеристики изменения численности трудовых ресурсов используются следующие относительные показатели: • коэффициент естественного пополнения трудовых ресурсов: % • коэффициент естественного выбытия трудовых ресурсов: % • коэффициент естественного прироста трудовых ресурсов: • коэффициент миграционного прироста: % Население, активное в данный период (или рабочая сила), — наи более часто используемый показатель, характеризующий численность экономически активного населения. Коэффициент экономической ак тивности населенияопределяется по формуле:, где — численность экономически активного населения на дату — t; — численность всего населения на ту же дату. На основе данных о численности занятого населения и экономи чески активного населения рассчитывается коэффициент занятости населения: где — численность занятых на дату. Коэффициент занятости рассчитывается как по населению в це лом, так и по полу и отдельным возрастным группам. К безработнымотносятся лицаот16 лет и старше, которые в тече ние рассматриваемого периода [1]: • не имели работы либо занятия, приносящего доход; • искали работу; • готовы были приступить к работе. При отнесении того или иного лица к категории безработных долж ны учитываться все три указанных критерия. Для характеристики уровня безработицы исчисляется коэффици ент безработицы: где — численность безработных на дату; Р — численность экономически активного населения на дату. Данные о безработице разрабатываются по полу, возрасту и семей ному положению. Изучается также распределение безработных по об разованию и профессиональной принадлежности. Списочная численность работников-это сумма работников, явив шихся и не явившихся по различным причинам. Явившиеся работники подразделяются на фактически работавших, т. е. приступивших к работе независимо от продолжительности рабочего дня, и не приступивших к работе независимо от причин, т. е. имевших целодневные простои. Не явившиеся (временно отсутствующие) работники подразделяют ся на основании причины неявок. Среднесписочная численность работниковза период определяется отношением [2]: где — сумма списочных чисел за период/число календарных дней в периоде. Средняя списочная численность работников за год находится по средней из средних списочных чисел за все месяцы. При этом, если предприятие работало неполный год, то сумма средних списочных численностей все равно делится на 12 месяцев.
№66
Национальное богатство представляет собой совокупность материальных благ, созданных трудом предшествующих и нынешнего поколений, а также природных ресурсов, разведанных и вовлеченных в экономический оборот, нематериальных активов и ценностей.
Категория «национальное богатство» используется для оценки экономического потенциала и уровня экономического развития страны, а также для международных сопоставлений. Система показателей статистики национального богатства включает в себя следующие основные характеристики:
1) наличия (объема) и структуры богатства;
2) воспроизводства важнейших его частей;
3) динамики всего богатства и его составных частей;
4) размещения богатства на территории страны;
5) охраны природных ресурсов и их восполнения.
Объем национального богатства исчисляется, как правило, в стоимостном выражении в текущих и сопоставимых ценах на определенный период времени (обычно на начало и конец года). Объем НБ в текущих ценах отражает стоимость его элементов в ценах приобретения соответствующих периодов. В сопоставимых ценах НБ отражает стоимость всех его элементов в це
|
|||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1064; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.17.175 (0.013 с.) |

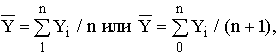
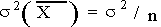 .
.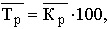
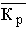 – средний коэффициент роста, рассчитанный как
– средний коэффициент роста, рассчитанный как 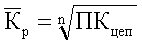 . Здесь Кцеп – цепные коэффициенты роста;
. Здесь Кцеп – цепные коэффициенты роста;


