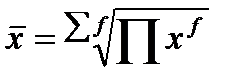Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 2. Абсолютные, относительные и средние величиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель: усвоить и закрепить материал по теме, научиться преобразовывать исходные данные в обобщающие показатели. Сводка статистических данных всегда завершается расчетом и анализом статистических показателей, в которых отражаются результаты исследования количественной стороны массовых общественных явлений. Статистический показатель - это количественная характеристика социально-экономических явлений и процессов в условиях качественной определенности, т. е. он непосредственно связан с внутренним содержанием изучаемого явления или процесса, его сущностью. По форме выражениявыделяют: абсолютные, относительные и средние показатели. Абсолютные показатели – это показатели, характеризующие абсолютные размеры изучаемых статистикой процессов и явлений в конкретных условиях места и времени: массу, площадь, объем, протяженность; отражают временные характеристики, а также могут представлять объем совокупности, т.е. число составляющих ее единиц. В статистике различают два вида абсолютных величин: индивидуальные и суммарные. Индивидуальные абсолютные величины характеризуют размеры признака у отдельных единиц совокупности, которые получают непосредственно в процессе статистического наблюдения, например, размер заработной платы отдельного работника, величина уставного капитала банка и т.д. Суммарные абсолютные величины характеризуют итоговую величину признака по определенной совокупности объектов, охваченным статистическим наблюдением, например, численность студентов г. Москвы. Абсолютные статистические показатели всегда являются именованными числами. В зависимости от социально-экономической сущности исследуемых явлений абсолютные показатели могут быть выражены в натуральных, стоимостных и трудовых единицах измерения. Натуральные единицы измерения в свою очередь могут быть: - простыми (тонны, килограммы, унции, квадратные, кубические и простые метры, мили, километры, галлоны, литры, миллилитры, декалитры (1дкл = 10л), гектолитры (1гкл = 100л), штуки, караты и т.д.); - сложными – представляют собой произведение двух простых единиц измерения (например, показатели грузооборота и пассажирооборота оцениваются соответственно в тонно-километрах и пассажиро-километрах, производство электроэнергии измеряется в киловатт-часах, и т.д.).
В группу натуральных также входят условно-натуральные измерители, используемые, когда какой-либо продукт имеет несколько разновидностей и общий объем можно определить только исходя из общего для всех потребительского свойства. Например, различные виды органического топлива переводятся в условное топливо с теплотой сгорания 29,3 МДж/кг (7000 Ккал/кг); мыло разных сортов - в условное мыло с 40%-м содержанием жирных кислот; консервы различного объема - в условные консервные банки объемом 353,4 см3 или массой 400 г; в консервной промышленности также принято вести учет продукции в тубах – 1000 условных банок и мубах – миллион условных банок; для алкогольной продукции используют дал а/а – декалитры абсолютного алкоголя, т.е. спирта, практически не содержащего воды. В полиграфии для учета печатной продукции используют условные печатные листы (1 п.л. = 40000 печатных знаков, включая пробелы). Для определения объема продукции в условно-натуральных единицах измерения (QУСЛ. НАТ..) следует объем продукции в натуральных единицах измерения (qНАТ) умножить на коэффициент пересчета (КПЕРЕСЧ): QУСЛ. НАТ.. = qНАТ * КПЕРЕСЧ Коэффициент пересчета определяется отношением
Стоимостные единицы измерения дают денежную оценку социально-экономическим явлениям и процессам. Например, стоимостные единицы часто используются для выражения объема разнородной продукции в стоимостной форме (валовой выпуск продукции). Трудовые единицы измерения позволяют учитывать как общие затраты труда на предприятии, так и трудоемкость отдельных операций (человеко-дни и человеко-часы). Типовая задача 1 В отчетном периоде предприятиями консервной промышленности района произведено продукции:
Определить общий объем производства консервов в отчетном периоде. Решение В данном случае консервы имеют разные единицы измерения, поэтому для определения их общего объема необходимо перевести весь выпуск консервов в условные банки массой 400 г или объемом 353,4 см3. Тогда получим:
- соус томатный: (535: 400) * 120 = 161 (усл. банок) - икра кабачковая: (510: 400) * 150 = 191 (усл. банок) - огурцы маринованные: (1000: 353,4) * 300 = 849 (усл. банок) - свинина тушеная: (800: 353,4) * 200 = 453 (усл. банок) - молоко сгущенное: (400: 400) * 500 = 500 (усл. банок) Общий выпуск: 161 + 191 + 849 + 453 + 500 = 2154 (усл. банок) Относительный показатель – это обобщающий показатель, который представляет собой результат деления одного абсолютного показателя на другой и выражает соотношение между количественными характеристиками социально-экономических процессов и явлений: текущий / сравниваемый показатель
основание / база сравнения Относительные показатели могут выражаться в коэффициентах, процентах, промилле, продецимилле или быть именованными числами. Все используемые на практике относительные статистические показатели можно разделить на следующие виды (табл. 2.1). Таблица 2.1
Типовая задача 2 На основе следующих данных определите различные виды относительных показателей, характеризующих производство зерна в фермерском хозяйстве.
Решение 1. Относительный показатель планового задания:
2. Относительный показатель выполнения плана:
3. Относительный показатель динамики:
4. Относительный показатель структуры:
для базисного периода: для отчетного периода: 5. Относительный показатель интенсивности:
в базисном периоде: в отчетном периоде: Средняя величина – это обобщающий показатель, характеризующий типичный уровень варьирующего признака в расчете на единицу однородной совокупности в конкретных условиях места и времени. Средняя величина всегда именованная, она имеет ту же единицу измерения, что и признак у отдельных единиц совокупности. В статистике применяют две категории средних: степенные и структурные. Степенные средние Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными.
Простая средняя вычисляется по несгруппированным данным и имеет следующий вид:
где хi – значение признака для единицы совокупности i, m – показатель степени средней, n – число единиц совокупности. Взвешенная средняя вычисляется по сгруппированным данным и имеет вид:
где хi – значение признака для единицы совокупности i, m – показатель степени средней, fi – частота, показывающая, сколько раз встречается i-е значение признака. Формулы расчета степенных средних имеют общий показатель степени m. В зависимости от того, какое значение он принимает, различают следующие виды степенных средних: 1. Средняя арифметическая (m=1) – наиболее распространенный вид средней.
Примечание. Если значения осредняемого признака заданы в виде интервалов, то при расчете средней арифметической величины в качестве значений признаков в группах принимают середины этих интервалов, в результате чего образуется дискретный ряд. При этом величины открытых интервалов условно приравниваются к интервалам, примыкающим к ним. Свойства средней арифметической: а) если все индивидуальные значения признака (все варианты) уменьшить или увеличить в m раз, то среднее значение соответственно уменьшится или увеличится в m раз. б) если все варианты осредняемого признака уменьшить или увеличить на число А, то средняя арифметическая соответственно уменьшится или увеличится на это же число А. в) если частоты (веса) всех осредняемых вариантов уменьшить или увеличить в k раз, то средняя арифметическая не изменится. 2. Средняя гармоническая (m=-1) – является величиной обратной для средней арифметической и применяется, когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение xf.
3. Средняя геометрическая (m=0) – применяется для определения средней по значениям, имеющим большой разброс, либо в случаях определения средней величины по относительным показателям, например, среднегодовых темпов роста в рядах динамики, где индивидуальные значения признака представляют собой коэффициенты роста:
4. Средняя квадратическая (m=2) – применяется, когда требуется определить средний размер признака, выраженный в квадратных единицах измерения (для вычисления средней стороны квадратных участков) или при расчете среднего квадратического отклонения, являющегося одним из показателей вариации признаков:
Если рассчитать все виды средних для одних и тех же исходных данных, то их значения окажутся неодинаковыми, т. к. здесь действует правиломажорантности средних: чем больше показатель m, тем больше средняя величина:
Структурные средние Структурные средние применяются для изучения внутреннего строения и структуры рядов распределения значений признака. В качестве структурных средних чаще всего используют показатели моды и медианы. 1. Мода – наиболее часто повторяющееся значение признака в изучаемой совокупности. Для дискретных рядов распределения модой будет то значение признака, у которого наибольший удельный вес. В интервальных рядах распределения с равными интервалами мода определяется по формуле: Мо = где i – величина модального интервала;
2. Медиана – величина признака, которая делит упорядоченную последовательность его значений на 2 равные по численности части. Если ряд распределения дискретный и имеет нечетное число значений, то медианой будет значение признака, находящееся в середине упорядоченного ряда. Например, стаж пяти рабочих составил 2, 4, 7, 8 и 10 лет. В таком упорядоченном ряду медиана – 7 лет. Если упорядоченный ряд состоит из четного числа значений, то медианой будет средняя арифметическая из 2 значений признака, расположенных в середине ряда. Пусть в бригаде не 5 человек, а 6, имеющих стаж работы 2, 4, 6, 7, 8 и 10 лет. В центре ряда стоят 6 и 7, т. е. средняя арифметическая этих значений и будет медианой ряда: Ме = (6+7)/2=6,5 лет. В интервальном вариационном ряду медиана определяется по формуле:
где
Нахождение медианы в интервальных вариационных рядах требует предварительного определения интервала, в котором находится медиана, т.е. медианного интервала – этот интервал характеризуется тем, что его кумулятивная частота равна полусумме или превышает полусумму всех частот ряда. Если значение средней величины совпадает с модой и медианой, то ряд является симметричным. На практике строго симметричные ряды встречаются довольно редко, чаще исследователю приходится иметь дело с асимметричными рядами. Если AS = Типовая задача 3 Известны следующие данные о реализации товара на рынках города:
Определить среднюю цену реализации товаров на каждом рынке отдельно. Решение 1. Определим среднюю цену реализации товаров на первом рынке. Т.к. данные уже сгруппированы, то используем формулу средней арифметической взвешенной, где х – цена товара, руб.; f - количество проданных товаров, т.
2. Определим среднюю цену реализации товаров на втором рынке. В данном случае отсутствуют частоты ряда (f), т.е. количество реализованных товаров, но известна их стоимость (w = xf), тогда для определения средней цены используем формулу средней гармонической:
Типовая задача 4 Известны следующие данные о незанятом населении города:
Вычислите: 1. средний возраст незанятого населения; 2. моду и медиану. Решение 1) Определим средний возраст незанятого населения. Т.к. исходные данные сгруппированы, то определим средний возраст по формуле средней арифметической взвешенной: Определим xi как середины интервалов (см. примечание).
Тогда 2) Определим моду и медиану. Т.к. исходные данные заданы интервальным рядом распределения, то мода и медиана определяются по формулам. а) мода:
Сначала определим интервал, который содержит моду. Т.к. мода – это значение признака, которое имеет наибольшую частоту, то найдем fmax. fmax. = 71, значит, мода содержится в интервале от 35 до 45 лет, тогда
б) медиана:
Определим интервал, содержащий медиану. Медианным интервалом считается тот, для которого сумма накопленных частот составляет больше половины всей численности ряда. Половина численности ряда 0,5 Сумма накопленных частот первого интервала равна 15, то есть она меньше половины частот ряда (95). Сумма накопленных частот второго интервала 15+37=52 тоже меньше половины частот ряда 95. Сумма накопленных частот третьего интервала 15+37+71=123 превышает половину численности ряда 95, значит, медиана находится в интервале от 35 до 45 лет, тогда:
Задачи для самостоятельной работы Задача 2.1 За отчетный период фабрикой выпущены тетради:
Определите общий выпуск тетрадей в натурально-условном выражении (в пересчете на тетради 12 листов). Задача 2.2 Добыча нефти и угля в РФ в 1999 – 2001 гг. характеризуется следующими данными:
Сделайте пересчет в условное топливо и проведите анализ изменения совокупной добычи этих ресурсов. Задача 2.3 Поставка молочной продукции в торговую сеть города характеризуется следующими данными:
Определите объем поставки молочной продукции в торговую сеть города по плану и фактически в условно-натуральном выражении (в пересчете на молоко 3,2%-ной жирности). По каждому виду продукции и в целом по ассортименту определите относительные показатели реализации плана. Представьте результаты в виде статистического графика и укажите его вид. Задача 2.4 По состоянию на конец 2004г. на учете в органах социальной защиты региона состояло 307,6 тыс. пенсионеров, из них 226,5 тыс. чел. – по старости. Для сравнения на конец 2003г. эти же показатели соответственно составили 310,1 и 228,6 тыс. чел. Средний размер назначенной месячной пенсии с учетом компенсационных выплат составил в 2004г. – 1942,4 руб., в том числе по старости – 2135,6 руб. (в 2003г. соответственно – 1702,6 и 1865,8 руб.). Для сравнения – средняя заработная плата работающих в 2004г. составила – 5012 руб., прожиточный минимум пенсионеров – 1632,3 руб. Для характеристики пенсионного обеспечения в области рассчитайте относительные величины динамики, структуры и сравнения. Сделайте выводы. Задача 2.5 Известны следующие данные об ассортименте продукции одного из предприятий:
1. Определить абсолютное отклонение стоимости продукции от плана и процент выполнения плана по стоимости продукции для отдельных ее видов. 2. Определить относительные показатели структуры выпуска продукции по плану и фактически. 3. Определить среднюю цену единицы продукции по плану и фактически 4. Сделать выводы. Задача 2.6 На основе исходных данных о выпуске продукции 3-х цехов определить: - относительную величину динамики по производству продукции в целом, - рассчитать среднегодовой темп роста выпуска продукции по каждому цеху, - определить средний выпуск продукции в год по каждому цеху.
Задача 2.7 Определить средний расход сырья в базисном и отчетном периоде, обосновать выбор формулы средней величины.
Задача 2.8 Выпуск продукции двумя цехами предприятиями характеризуется следующими данными:
Определите в целом по предприятию средний удельный вес продукции I сорта. Задача 2.9 Известны данные о финансовых показателях предприятий за два периода:
Определите среднюю прибыль на одну акцию по двум предприятиям в каждом периоде. Задача 2.10 Известны данные о кредитных операциях банков за отчетный период:
Определите среднюю процентную ставку по каждому виду кредита в целом по двум банкам. Задача 2.11 В ходе бизнес планирования стало известно, что максимальная сумма прибыли организуемого предприятия быстрого питания в первый месяц работы может составить 1 млн. руб., а минимальная – 10 тыс. руб. Определите среднюю сумму прибыли. Задача 2.12 Страховая компания предлагает приобрести страховой полис на 5 лет с ежегодным доходом 3, 5, 7, 9 и 12%. Определите средний процент дохода владельца страхового полиса. Задача 2.13 По приобретенной ценной бумаге со сроком погашения через три года доходность составит в каждый год соответственно 10, 12 и 15% годовых. Определите среднюю доходность ценной бумаги. Задача 2.14 На основе исходных данных создать интервальный вариационный ряд распределения рабочих по уровню производительности труда, по данным которого определить: - средний уровень производительности труда - структурные средние, изобразить их графически.
Задача 2.15 Распределение торговых фирм по размеру товарооборота характеризуется следующими данными:
Определите: а) средний размер товарооборота на одну фирму; б) модальное и медианное значение товарооборота; в) сделайте вывод о симметрии данного ряда распределения. Задача 2.16 Имеются следующие данные специального статистического обследования потоков покупателей в один из дней работы супермаркета:
Определить моду и медиану. Сделайте выводы. Задача 2.17 Известны данные о распределении рабочих одного цеха предприятия по величине годовой выработки:
Определите среднюю годовую выработку на одного рабочего: Изобразите ряд распределения в виде полигона, гистограммы и кумуляты. Определите моду и медиану по формулам и графически. Сделайте выводы. Тестовые задания 1. Абсолютные величины выражаются в.... A. натуральных единицах измерения; B. процентах; C. денежных единицах измерения; D. виде простого кратного отношения; E. трудовых единицах измерения. 2. Взаимосвязь относительных показателей динамики (ОПД), планового задания (ОППЗ) и реализации плана (ОПРП) выражается соотношением: A. ОПД = ОППЗ х ОПРП; B. ОПД = ОППЗ: ОПРП; C. ОППЗ = ОПД х ОПРП; D. ОПРП = ОПД х ОППЗ. 3. Назовите абсолютные статистические показатели из ниже перечисленных: A. 1500 рублей; B. 15%; C. 3 о/оо; D. 10 чел. на 1 кв. м; E. 350 м2 4. Укажите относительные показатели, которые могут быть выражены именованными числами: A. динамики; B. реализации плана; C. интенсивности и уровня экономического развития; D. структуры. 5. Если модальное значение признака больше средней величины признака, то это свидетельствует о.... A. правосторонней асимметрии в данном ряду распределения; B. левосторонней асимметрии в данном ряду распределения; C. нормальном законе распределения; D. биномиальном законе распределения; E. симметричности распределения. 6. Для характеристики структуры совокупности статистика рекомендует вычислить: A. коэффициент роста; B. долю частей в общем итоге; C. модальную и медианную величины; D. относительную величину интенсивности; E. относительную величину координации. 7. Величина средней арифметической при увеличении всех значений признака в 2 раза.... A. увеличится более чем в 2 раза; B. уменьшится более чем в 2 раза; C. не изменится; D. увеличится в 2 раза; E. уменьшится в 2 раза. 8. Медиана находится: A. в средине ряда распределения; B. в начале ряда распределения; C. в конце ряда распределения; D. делит ряд пополам. 9. Среднегодовой коэффициент роста в рядах динамики исчисляется по формуле: A. средней геометрической; B. средней гармонической; C. средней кубической; D. средней арифметической. 10. Установите соответствие: A. средняя арифметическая простая 1. B. средняя арифметическая взвешенная 2. C. средняя гармоническая простая 3. D. средняя квадратическая простая 4. E. средняя геометрическая простая 5. Домашнее задание Прочтите справочную информацию о натуральных величинах, приведенную ниже. Подготовьте аналогичный доклад о таких величинах, как: а) морская и сухопутная мили; б) тройская унция и карат; в) ярд, фут и дюйм; г) унция, драхма, стоун и фунт; д) длинная и короткая тонны. Галлон — мера объёма, применяемая в странах, где исторически сложилась система мер и весов, отличная от метрической. Обычно используется для жидкостей, в редких случаях — для твёрдых тел. Галлон изначально определялся как объём 8 фунтов пшеницы. Позже другие разновидности были введены в обиход для других продуктов и, соответственно, появились новые варианты. Америка приняла британский винный галлон, определённый в 1707 году как 231 кубический дюйм или 3,785 л, в качестве основной меры объёма жидкости. Отсюда была выведена американская жидкая пинта (0,473 л). Пинта является производной величиной от галлона — одна восьмая его часть. Был также принят британский кукурузный галлон (268,8 кубического дюйма или) как мера объёма сыпучих тел. Отсюда произошла американская сухая пинта для измерения сыпучих продуктов (0,55 л). 42 американских галлона (159 л) составляют 1 американский баррель. Эта величина применяется для измерения нефти. Однако при измерении объёма пива (из-за налоговых ограничений) в США используется, так называемый, стандартный пивной баррель, который равен 31,5 американскому галлону (119,24 л). Кроме того, в США галлоны используются для измерения веса: - мёда - 0,443 кг - оливкового масла - 3,447 кг - сыпучих тел - 4,405 кг В Великобритании в 1824 году британский парламент заменил все варианты галлона на один имперский галлон, определённый как 10 фунтов дистиллированной воды при температуре 62 °F (277,42 кубического дюйма или 4,546 л). Для измерения спирта в Британии используется пруф-галлон (2,594 л). В других странах мира приняты следующие меры галлона: Аргентина - 3,80 л Куба - 3,785 л
Лошадиная сила (л. с.) — единица измерения мощности. Учёные очень редко пользуются этой единицей из-за её неоднозначного определения, но несмотря на это, она получила широкое распространение, особенно в автомобильной индустрии. Стандартной единицей системы СИ для измерения мощности является ватт. Лошадиная сила впервые предложена Джеймсом Уаттом, оценивающим мощность своих паровых двигателей. Предполагалось, что лошадь может поднимать в среднем 33 000 фунт-футов в минуту (например, 330 фунтов (150 кг) со скоростью 100 футов (30 м) в минуту), что равняется 745,69987158227022 Вт. Эту единицу до сих пор применяют в англоязычных странах (обозначение HP). В большинстве европейских стран, в том числе в России, лошадиная сила определяется как 75 кг·м/с, что составляет ровно 735,49875 Вт (иногда это называют «метрическая лошадиная сила»; обозначение PS (нем.), CV (фр.), pk (нид.)).
Глава 3. Вариация признака Цель: усвоить и закрепить материал по теме, научиться проводить анализ вариационных рядов. Вариация – это различие в значениях какого-либо признака у разных единиц совокупности в
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 2034; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.174.204 (0.02 с.) |


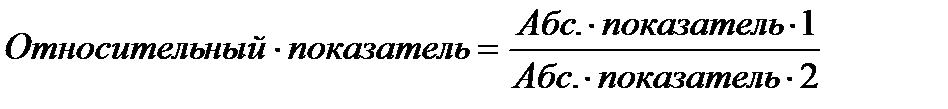

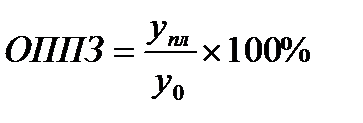 ,
где yпл. ¾ уровень, запланированный на будущий период;
y0 ¾ уровень, фактически сложившейся в прошлом.
,
где yпл. ¾ уровень, запланированный на будущий период;
y0 ¾ уровень, фактически сложившейся в прошлом.
 ,
где y1 ¾ фактически достигнутый уровень в текущем периоде;
yпл.¾ уровень, запланированный на этот же период.
Между относительными показателями планового задания, реализации плана и динамики существует следующая взаимосвязь:
ОППЗ ´ ОПРП = ОПД.
,
где y1 ¾ фактически достигнутый уровень в текущем периоде;
yпл.¾ уровень, запланированный на этот же период.
Между относительными показателями планового задания, реализации плана и динамики существует следующая взаимосвязь:
ОППЗ ´ ОПРП = ОПД.




 , т.е. фермерское хозяйство запланировало увеличить валовой сбор зерна на 2,5% по сравнению с фактически достигнутым уровнем базисного периода.
, т.е. фермерское хозяйство запланировало увеличить валовой сбор зерна на 2,5% по сравнению с фактически достигнутым уровнем базисного периода. , т.е. план по производству зерна в фермерском хозяйстве был перевыполнен на 7,5%.
, т.е. план по производству зерна в фермерском хозяйстве был перевыполнен на 7,5%. или 110,2%, т.е. валовой сбор зерна в отчетном периоде по сравнению с базисным увеличился на 10,2%.
или 110,2%, т.е. валовой сбор зерна в отчетном периоде по сравнению с базисным увеличился на 10,2%.
 , т.е. в базисном периоде зерновые занимали 51,06% от всей посевной площади;
, т.е. в базисном периоде зерновые занимали 51,06% от всей посевной площади; , т.е. в отчетном периоде доля зерновых снизилась до 40% от общей площади.
, т.е. в отчетном периоде доля зерновых снизилась до 40% от общей площади. (т/га);
(т/га); (т/га).
(т/га).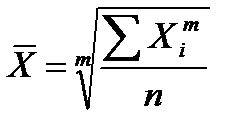 ,
,  ,
, 


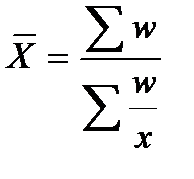 ,
где w = xf
,
где w = xf




 .
. ,
, - начальное значение интервала, содержащего моду;
- начальное значение интервала, содержащего моду; - частота модального интервала (в абсолютном или относительном выражении);
- частота модального интервала (в абсолютном или относительном выражении); - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному; - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным. ,
, - начальное значение интервала, содержащего медиану;
- начальное значение интервала, содержащего медиану; - величина медианного интервала;
- величина медианного интервала; - сумма частот ряда;
- сумма частот ряда;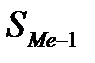 - сумма накопленных частот, предшествующих медианному интервалу;
- сумма накопленных частот, предшествующих медианному интервалу; - частота медианного интервала.
- частота медианного интервала. <0, то в ряду имеет место левосторонняя асимметрия, если AS =
<0, то в ряду имеет место левосторонняя асимметрия, если AS = 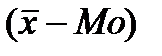 >0, то – правосторонняя.
>0, то – правосторонняя. (руб.)
(руб.) (руб.)
(руб.) .
. (года)
(года) .
.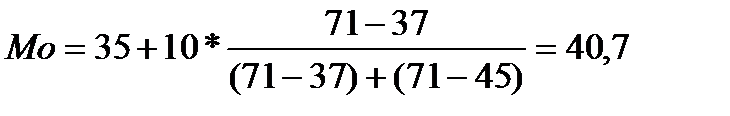 (лет), т.е. большинство безработных имеют возраст около 41 года.
(лет), т.е. большинство безработных имеют возраст около 41 года.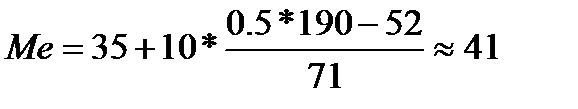 (год), т.е. половина безработных младше 41 года, а вторая половина – старше 41 года.
(год), т.е. половина безработных младше 41 года, а вторая половина – старше 41 года.