
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непараметрические показатели связиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В статистической практике встречаются такие ситуации, когда значения факторных и результативных признаков не могут быть выражены численно. В этом случае для измерения тесноты зависимости необходимо использовать так называемые непараметрические методы. Наибольшее распространение имеют ранговые коэффициенты корреляции, в основу которых положен принцип нумерации значений статистического ряда. При использовании коэффициентов корреляции рангов коррелируют не сами значения показателей х и у, а только номера их мест, которые они занимают в каждом ряду значений. В этом случае номер каждой отдельной единицы будет ее рангом. Коэффициенты корреляции, основанные на использовании ранжированного метода, были предложены К. Спирмэном и М. Кендэлом. Коэффициент корреляции рангов Спирмэна (р) основан на рассмотрении разности рангов значений результативного и факторного признаков и может быть рассчитан по формуле
где d = Nx - Ny, т.е. разность рангов каждой пары значений х и у; n - число наблюдений. Ранговый коэффициент корреляции Кендэла (
где S = P + Q. К непараметрическим методам исследования можно также отнести коэффициент ассоциации kас и коэффициент контингенции kкон, которые используются, если, например, необходимо исследовать тесноту зависимости между качественными признаками, каждый из которых представлен в виде альтернативных признаков. Для определения этих коэффициентов создается расчетная таблица (таблица «четырех полей»), где статистическое сказуемое схематически представлено в следующем виде (табл. 8.2). Таблица 8.2
Здесь а, b, c, d - частоты взаимного сочетания (комбинации) двух альтернативных признаков Коэффициент ассоциации можно рассчитать по формуле:
Коэффициент ассоциации изменяется от -1 до +1. Чем ближе его значение к +1 или к -1, тем сильнее связаны между собой изучаемые признаки. Коэффициент контингенции рассчитывается по формуле:
Нужно иметь в виду, что для одних и тех же данных коэффициент контингенции (изменяется от -1 до +1) всегда меньше коэффициента ассоциации. Если необходимо оценить тесноту связи между альтернативными признаками, которые могут принимать любое число вариантов значений, применяется коэффициент взаимной сопряженности Пирсона (КП).
Для исследования такого рода связи первичную статистическую информацию располагают в форме таблицы (табл. 8.3). Таблица 8.3
Здесь mij - частоты взаимного сочетания двух атрибутивных признаков; П - число пар наблюдений. Коэффициент взаимной сопряженности Пирсона определяется по формуле
где
Коэффициент взаимной сопряженности изменяется от 0 до 1. Наконец, следует упомянуть коэффициент Фехнера, характеризующий элементарную степень тесноты связи, который целесообразно использовать для установления факта наличия связи, когда существует небольшой объем исходной информации. Данный коэффициент определяется по формуле
где na - количество совпадений знаков отклонений индивидуальных величин от их средней арифметической; nb - соответственно количество несовпадений. Коэффициент Фехнера может изменяться в пределах -1,0 Вопросы для самоконтроля 1. Что подразумевает под собой исследование взаимосвязей между явлениями в статистике? 2. Какие типы связей между явлениями Вы знаете? 3. Какие методы моделирования связи используют в статистике? 4. Какие основные задачи решают с помощью корреляционного и регрессионного анализа? 5. Что собой представляет корреляционная связь? 6. Расскажите правила построения однофакторной регрессионной модели. В чем состоит значение уравнения регрессии? 7. Какой экономический смысл имеют коэффициенты эластичности? 8. Какими показателями измеряется теснота корреляционной связи? 9. В чем назначение нелинейных и многофакторных уравнений регрессии? Какие нелинейные модели регрессии Вы знаете? 10. Охарактеризуйте правила построения множественной регрессии. 11. Какие непараметрические методы применяют для моделирования связи между явлениями?
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 639; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.178.162 (0.011 с.) |


 ) можно определить по формуле:
) можно определить по формуле:
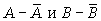 ; n - общая сумма частот.
; n - общая сумма частот.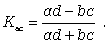


 - показатель средней квадратической сопряженности:
- показатель средней квадратической сопряженности: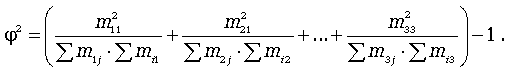

 kф
kф 


