
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение вероятности в выборках в зависимости от величины t и объема выборки nСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Примечание При оценке результатов малой выборки (численность которой не превышает 30 единиц), величина генеральной дисперсии в расчетах не используется. Величина
где На заключительном этапе на основе предельной ошибки выборки определяют доверительные интервалы, в которых может находиться генеральная средняя или генеральная доля. Выход за пределы этой области имеет весьма малую вероятность. Доверительные интервалы определяются по формулам: § для среднего значения: § для доли: Типовая задача 1 Для анализа выполнения норм выработки предприятия было проведено 10%-ное механическое повторное выборочное обследование, результаты которого показали следующее распределение рабочих по выполнению норм выработки:
Определить: 1) с вероятностью 0,954 возможные пределы, в которых ожидается средний процент выполнения норм выработки по предприятию; 2) с вероятностью 0.997 возможные пределы доли рабочих, выполняющих нормы выработки на 100% и более, в общей численности предприятия. Решение 1) Определим возможные пределы среднего выполнения норм выработки по предприятию, т.е. доверительный интервал Сначала определим выборочную среднюю:
Т.к. отбор единиц в выборку по условию бесповторный, то определим величину предельной ошибки выборки по формуле:
t = 2 (при p = 0,954); n = 100 (чел.);
Следовательно, определим границы доверительного интервала: (98,7-2,1; 98,7+2,1) (96,6; 100,8). Таким образом, с вероятностью 0.954 можно утверждать, что среднее выполнение норм выработки по всему предприятию изменяется от 96,6 до 100,8%. 2) Определим возможные пределы доли рабочих, выполняющих нормы выработки сверх плана, т.е. доверительный интервал: Рассчитаем долю рабочих, выполняющих план на 100% и более. По условию таких рабочих 51 человек, значит:
Т.к. отбор единиц в выборку по условию бесповторный, то определим величину предельной ошибки выборки по формуле:
Определим границы доверительного интервала: (51-14; 51+14) (37; 65) Таким образом, с вероятностью 0.997 можно утверждать, что доля рабочих, выполняющих план на 100% и более, в общей численности предприятия изменяется от 37 до 65%. При проектировании выборочного наблюдения с заранее заданным значением допустимой ошибки выборки важно правильно определить численность (объем) выборочной совокупности, которая с определенной вероятностью обеспечит заданную точность результатов наблюдения. Для этого используют следующие формулы расчета (табл. 4.3). Таблица 4.3
Отметим, что с увеличением предельной ошибки уменьшается необходимый объем выборки, и наоборот. Типовая задача 2 Сколько домохозяйств, состоящих из 2 человек, необходимо охватить обследованием, чтобы вычислить их средние расходы в месяц с предельной ошибкой 150 руб. и уровнем вероятности 0,997, если известно, что в городе 500 домохозяйств, состоящих из 2 человек, а дисперсия расходов, по данным прошлогоднего обследования, составляет 25000 руб. Решение Объем выборки определим по формуле:
t = 3 (при р = 0,997);
Задачи для самостоятельной работы Задача 4.1 Известны данные случайного повторного выборочного обследования о распределении вкладчиков по размеру вкладов в банк города:
Определить с вероятностью 0,954: 1) пределы среднего размера вклада в банк; 2) пределы удельного веса вкладов с размером более 100 тыс. руб.; Сделать выводы. Задача 4.2 При 30-% механической бесповторной выборке рабочих были получены следующие исходные данные:
Определить: 1) среднюю производительность труда по предприятию в целом с вероятностью 0,954; 2) долю женщин, работающих в организации, в общей численности рабочих с вероятностью 0,997. Сделать выводы. Задача 4.3 При 25-% механической бесповторной выборке были исследованы предприятия по уровню прибыльности:
На основе исходных данных определить: 1. Средний уровень прибыли (убытка) в целом по отрасли с вероятностью 0,954. 2. Долю убыточных предприятий в целом по отрасли, с вероятностью 0,997. Задача 4.4 В целях изучения производительности четырех типов станков, производящих одинаковые операции, была произведена 10%-ная типическая выборка (внутри групп применялся метод случайного бесповторного отбора). Результаты выборки представлены в таблице:
С вероятностью 0,997 определите предел, в котором находится среднее число деталей, производимых на одном станке за 1 час работы для всей совокупности станков. Задача 4.5 При выборочном собственно-случайном отборе получены следующие данные о недовесе укомплектованной продукции в ящиках весом 20 кг:
Определите средний недовес ящиков и с вероятностью 0,954 установите возможные пределы выборочной средней для всей партии, состоящей из 900 единиц; с вероятностью 0,683 определите пределы отклонения доли ящиков с недовесом до 1 кг. Какова должна быть численность выборки, чтобы ошибка доли не превышала 0,06 (с вероятностью 0,954)? Задача 4.6 Для изучения уровня жизни населения района необходимо провести выборочное наблюдение методом случайного повторного отбора. Сколько домохозяйств надо отобрать для обследования, чтобы с вероятностью 0,954 ошибка доли семей с доходами ниже прожиточного минимума не превышала 5%, если дисперсия доли равна 0,24? Задача 4.7 Определить, какое количество фирм должна проверить налоговая инспекция, чтобы с вероятностью 0,954 ошибка доли фирм, несвоевременно уплачивающих налоги, не превышала 5%? Предыдущая проверка показала, что доля таких организаций составила 25%. Задача 4.8 С целью определения среднего времени поездки работников предприятия на работу предполагается провести выборочное обследование по методу бесповторного отбора. Какова должна быть численность выборки, чтобы с вероятностью 0,988 ошибка выборки не превышала 5 минут при среднеквадратическом отклонении, равном 20 минутам. Известно, что численность работников предприятия составляет 1510 человек. Задача 4.9 На предприятии 4000 рабочих. Из них 3000 со стажем более 5 лет. С целью определения доли рабочих завода, не выполняющих норму выработки, предполагается провести типическую выборку рабочих. Отбор внутри типов механический. Какое количество рабочих необходимо отобрать, чтобы с вероятностью 0,954 ошибка выборки не превышала 5%. Из предыдущих исследований известно, что дисперсия типической выборки равна 900. Задача 4.10 На склад поступило 100 ящиков готовых изделий по 80 шт. в каждом. Для установления среднего веса изделия необходимо провести серийную выборку методом механического отбора так, чтобы с вероятностью 0,954 ошибка выборки не превышала 2г. Сколько изделий требуется отобрать, если из предыдущих исследований известно, что дисперсия серийной выборки равна 4. Тестовые задания 1. Расхождение между расчётными значениями признака в выборочной совокупности и действительными значениями признака в генеральной совокупности – это: A. ошибка репрезентативности; B. ошибка регистрации; C. ошибка метода расчёта; D. ошибка вычислительного устройства. 2. Если при отборе попавшая в выборку единица не возвращается в совокупность, то такой метод называется: A. индивидуальный отбор; B. повторный отбор; C. комбинированный отбор; D. бесповторный отбор. 3. Уменьшить предельную ошибку выборки можно за счет: A. увеличения численности выборки: B. уменьшения численности выборки; C. увеличения вероятности, гарантирующей результаты выборочного обследования; D. уменьшения вероятности, гарантирующей результаты выборочного обследования. 4. Объем повторной случайной выборки увеличится в... раза, если среднее квадратическое отклонение увеличится в 2 раза. 5. По способу формирования выборочной совокупности различают выборку: A. собственно-случайную; B. механическую; C. комбинированную; D. типическую (районированную); E. сложную; F. серийную; G. альтернативную. 6. Недостающим элементом в формуле расчета объема выборки при бесповторном случайном отборе (оценивается среднее значение признака):
является: A. B. C. (1- D. (N-1). 7. Репрезентативность результатов выборочного наблюдения зависит от: A. вариации признака; B. объема выборки; C. определения границ объекта исследования; D. времени проведения наблюдения; E. продолжительность проведения наблюдения. 8. Под выборочным наблюдением понимают: A. сплошное наблюдение всех единиц совокупности; B. несплошное наблюдение части единиц совокупности; C. несплошное наблюдение части единиц совокупности, отобранных случайным способом; D. наблюдение за единицами совокупности в определенные моменты времени; E. обследование наиболее крупных единиц изучаемой совокупности. 9. Преимущества выборочного наблюдения по сравнению со сплошным наблюдением: A. более низкие материальные затраты; B. возможность провести исследования по более широкой программе; C. снижение трудовых затрат за счет уменьшения объема обработки первичной информации; D. возможность периодического проведения обследований. 10. При проведении выборочного наблюдения определяют: A. численность выборки, при которой предельная ошибка не превысит допустимого уровня; B. число единиц совокупности, которые остались вне сплошного наблюдения; C. тесноту связи между отдельными признаками, характеризующими изучаемое явление; D. вероятность того, что ошибка выборки не превысит заданную величину; E. величину возможных отклонений показателей генеральной совокупности от показателей выборочной совокупности.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1907; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 и предельная ошибка малой выборки вычисляются на основе данных выборочного наблюдения:
и предельная ошибка малой выборки вычисляются на основе данных выборочного наблюдения: и
и 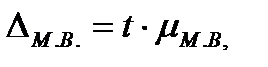 ,
, - мера случайных колебаний выборочной средней в малой выборке, а
- мера случайных колебаний выборочной средней в малой выборке, а 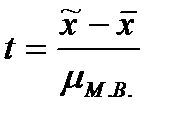 .
. ;
; .
. .
. , где
, где , т.к. по условию выборка 10%-ная, т.е. n составляет 10% от общей численности рабочих;
, т.к. по условию выборка 10%-ная, т.е. n составляет 10% от общей численности рабочих; Получим
Получим  .
. или 51%.
или 51%. , где t = 3 (при p = 0,997), тогда получим
, где t = 3 (при p = 0,997), тогда получим или 14%.
или 14%.

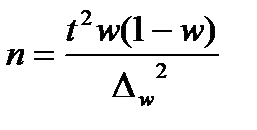




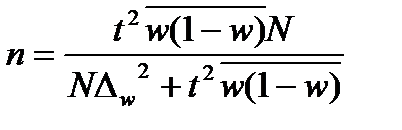




 , где
, где (руб.);
(руб.);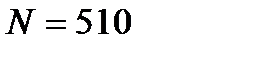 ;
; , тогда получим
, тогда получим домохозяйств.
домохозяйств.
 ;
; ;
;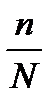 );
);


