Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон распределения вероятностей дискретной двумерной величиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Закон распределения дискретной двумерной случайной величины – перечень возможных значений этой величины, т.е. пары чисел
События (Х=
Функции распределения двумерной случайной величины
Функцией распределения двумерной случайной величины (X, Y) называют Свойства: 1. 2. 3. Предельные соотношения: 4. При
Вероятность попадания случайной величины в полуполосу И прямоугольник
Найдем вероятность того, что в результате испытания случайная точка попадет в полуполосу: Функция распределения Рассмотрим вероятность попадания в прямоугольник ABCD, заданий уравнениями сторон:
 
Плотность совместного распределения вероятностей непрерывной двумерной случайной величины
Непрерывную двумерную случайную величину можно также задать, пользуясь плотностью распределения. Будем предполагать, что функция распределения Двумерная плотность распределения вероятностей – вторая смешанная частная производная от функции Геометрически – это поверхность (поверхность распределения). Зная плотность распределения Вероятностный смысл f(x, y)
Вероятность попадания случайной точки в прямоугольник ABCD: Перейдем к пределу Свойства 1) f (x,y)³0 (F(x,y), поскольку 2)
Вероятность попадания случайной точки в произвольную область
Раздел IX. Элементы математической статистики Глава 23. Статическая оценка параметров распределения Задачи математической статистики. Вариационный ряд
Первая задача статистики – указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или экспериментов. Вторая задача – разработать методы анализа статистических данных в зависимости от целей исследования: а) оценка неизвестной вероятности события, известной функции распределения, параметров распределения, вид которого известен и т.д. б) проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен. Для исследования какого-либо признака из генеральной совокупности (всех объектов) извлекают выборку – случайно отображенные объекты.
Вариационный ряд Рассмотрим пример. Токарь изготавливал в течение 10 дней следующее количество деталей: 5,6,5,7,7,7,8,5,6,5. Ранжируем эту выборку – разобьем на группы: 5,5,5,5 6,6 7,7,7 8 4 раза 2 раза 3 раза 1 раз. При ранжировании группы располагаются в порядке возрастания. Значение каждой группы называется вариантой. Число повторений в каждой группе называется частотой варианты. Полученную таблицу называют вариационным рядом.
В общем виде:
Графическое изображение вариационного ряда – полигон. Для непрерывного признака весь интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала ni – сумму частот вариант, попавших в i -й интервал. Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны
Точечные оценки
Вариационный ряд характеризует случайную величину, но не в полной мере, поэтому используются характеристики, аналогичные теоретическим – М (х), D (х) и т.д. Эти числовые характеристики подсчитываются на основании выборки и называются точечными оценками (т.к. являются числами). Точечной оценкой характеристики Q называется некоторая функция Q* результатов наблюдений, значение которой принимают за приближение этой характеристики: 1. Несмещенность оценки: точечная оценка называется несмещенной, если ее математическое ожидание равно оценивающему параметру: 2. Состоятельность: точечная оценка называется состоятельной, если она при 3. Эффективность: точечная оценка считается эффективной, если она имеет (при заданном n) наименьшую дисперсию.
Основные точечные оценки
Выборочная средняя 2. Выборочная дисперсия: 3. Начальные и центральные моменты k - го порядка. Начальный момент k -го порядка:
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 678; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.125.137 (0.008 с.) |

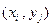 и их вероятностей
и их вероятностей 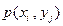
 .
.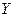

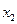
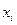

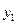




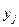




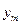




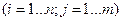 образуют полную группу, поэтому сумма вероятностей, помещенных в таблице, равна 1. Можно найти законы распределения каждой составляющей. События (Х=
образуют полную группу, поэтому сумма вероятностей, помещенных в таблице, равна 1. Можно найти законы распределения каждой составляющей. События (Х= 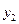 ),…,(Х=
),…,(Х=  - вероятность того, что Х примет значение
- вероятность того, что Х примет значение  – просуммировать вероятности «столбца
– просуммировать вероятности «столбца 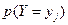 равно сумме вероятности строки
равно сумме вероятности строки 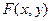 , определяющую вероятность того, что X<x, Y<y: F (x,y) =P (X < x, Y < y).
, определяющую вероятность того, что X<x, Y<y: F (x,y) =P (X < x, Y < y).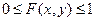 – вероятность.
– вероятность.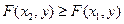 , если
, если 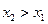 ;
; 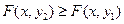 если
если 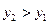 .
.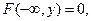
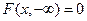 ,
, 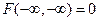 ,
, 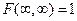 .
. ,
, 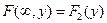 .
.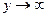 функция распределения системы
функция распределения системы 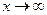 функция распределения системы становится функцией распределения составляющей Y.
функция распределения системы становится функцией распределения составляющей Y.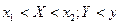 или в полуполосу
или в полуполосу 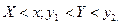
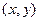 . Тогда вероятность попадания случайной точки в полуполосу равна:
. Тогда вероятность попадания случайной точки в полуполосу равна: 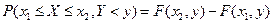 - это разность вероятностей попадания случайной точки в квадрант с вершиной
- это разность вероятностей попадания случайной точки в квадрант с вершиной 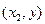 и вероятности попадания случайной точки в квадрант с вершиной
и вероятности попадания случайной точки в квадрант с вершиной 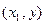 . Аналогично,
. Аналогично, 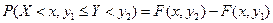 . Вероятность попадания случайной точки в полуполосу равна приращению функции распределения по одному из аргументов.
. Вероятность попадания случайной точки в полуполосу равна приращению функции распределения по одному из аргументов.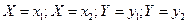 . Эта вероятность равна разности вероятности попадания случайной точки в полуполосу АВ и вероятность попадания случайной точки в полуполосу CD:
. Эта вероятность равна разности вероятности попадания случайной точки в полуполосу АВ и вероятность попадания случайной точки в полуполосу CD: 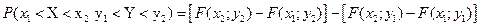 .
. Y
Y




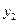

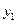


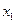
 X
X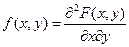 .
.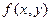 , можно найти функцию распределения
, можно найти функцию распределения 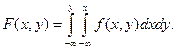
 . Применим теорему Лагранжа:
. Применим теорему Лагранжа: 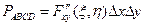 , где
, где 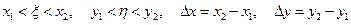 . Отсюда
. Отсюда 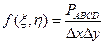 – это отношение вероятности попадания в квадрат к его площади.
– это отношение вероятности попадания в квадрат к его площади.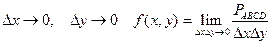 .
.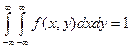 .
. – это вероятность попадания случайной точки в прямоугольник со сторонами
– это вероятность попадания случайной точки в прямоугольник со сторонами  и
и 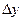 . Разобьем область D на n элементарных областей прямыми, параллельными Оу и Ох на расстоянии Dх и Dу. Вероятность попадания случайной точки в область D равна сумме вероятностей попадания точки в элементарные области:
. Разобьем область D на n элементарных областей прямыми, параллельными Оу и Ох на расстоянии Dх и Dу. Вероятность попадания случайной точки в область D равна сумме вероятностей попадания точки в элементарные области: 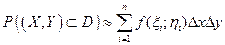 . Переходя к пределу, получим
. Переходя к пределу, получим 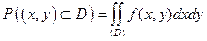 .
.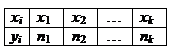
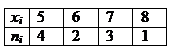
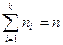 – объем выборки.
– объем выборки.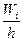 , где
, где 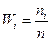 – относительная частота.
– относительная частота.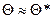 . Качество точечной оценки определяется характеристиками:
. Качество точечной оценки определяется характеристиками: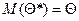 , т.е. совпадает с истинным значением.
, т.е. совпадает с истинным значением.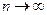 стремится по вероятности к оцениваемому параметру.
стремится по вероятности к оцениваемому параметру.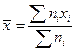 .
.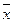 приближается к М (х), является несмещенной, состоятельной и эффективной.
приближается к М (х), является несмещенной, состоятельной и эффективной.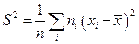 . S2 является состоятельной, но смещенной, поэтому часто используют несмещенную оценку – исправленную выборочную дисперсию:
. S2 является состоятельной, но смещенной, поэтому часто используют несмещенную оценку – исправленную выборочную дисперсию: 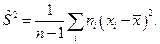
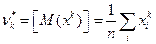 . Центральный момент k -го порядка:
. Центральный момент k -го порядка: