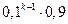Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретной случайной величиныСодержание книги
Поиск на нашем сайте
На практике часто встречаются величины, которые могут принимать некоторые значения, но нельзя достоверно предсказать, какое именно значение каждая из них примет в рассмотренном испытании. Например, число мальчиков, родившихся в Белгороде завтра, может быть различным: 0,1,2,3,4,…, n. Или – дальность полета снаряда, количество бракованных изделий в партии и т.д. Это – случайные величины. Случайной величиной называется переменная, которая может принимать те или иные значения, причем для каждого испытания она принимает единственное значение. Случайные величины обозначают заглавными буквами X, Y, Z,…, значения случайных величин соответственно малыми буквами. Случайные величины делятся на дискретные и непрерывные. Случайная величина называется дискретной, если множество ее значений конечно или счетное. Например, стрельба по мишеням из орудия до первого попадания (1,2,3,…, n, ¥). Или – количество бракованных деталей в партии из 30 изделий. Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного (или бесконечного) промежутка. Пусть Х – дискретная случайная величина, возможными и единственными значениями которой являются х 1, х 2, х 3,…, хn. Обозначим через Закон распределения дискретных случайных величин – соответствие между всеми значениями дискретных случайных величин и их вероятностями. Обычно его записывают в виде таблицы:
Если множество xi – бесконечно, то ряд Пример. Устройство состоит из 3 независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте. Возможные значения Х: x 1=0, x 2=1, x 3=2, x 3=3. Их вероятности определим по формуле Бернулли:
Биноминальное, геометрическое и гипергеометрическое Распределения Биноминальное распределение Пусть производится n независимых испытаний, в каждом из которых вероятность появления события постоянна и равна р. В качестве дискретной случайной величины Х рассмотрим число появления события А в этих испытаниях. Х может принимать значения 0,1,2,3,4,…, n с вероятностями, определенными по формуле Бернулли:
Полученная формула является аналитическим выражением биноминального закона распределения, т.е. биноминальным называется распределение вероятностей, определяемое формулой Бернулли. Запишем в виде таблицы:
Пример. Монета бросается два раза. Написать закон распределения дискретной случайной величины – числа появлений «герба». р = 0,5, q = 0,5,
Геометрическое распределение
Пусть проводятся независимые испытания, в каждом из которых вероятность появления события А равна р. Испытания заканчиваются, как только появится событие А, т.е. если событие появилось в k – ом испытании, то в предшествующих k – 1 испытаниях оно не появлялось. Пусть Х – дискретная случайная величина – число испытаний, которое нужно провести до появления события А. Очевидно, возможными значениями Х являются натуральные числа:
Очевидно, что Пример. Преподаватель задает дополнительные вопросы до первого неправильного ответа. Составить закон распределения случайной дискретной величины Х – числа дополнительных вопросов, если вероятность правильного ответа на вопрос равна 0,9.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 293; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.136.117 (0.01 с.) |

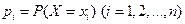 вероятность этих значений, т.е. рi есть вероятность того, что Х принимает значения xi. События Х = хi образует полную группу, поэтому
вероятность этих значений, т.е. рi есть вероятность того, что Х принимает значения xi. События Х = хi образует полную группу, поэтому 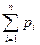 =1.
=1.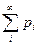 - сходится.
- сходится.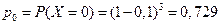 ,
, 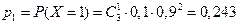
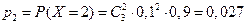 ,
, 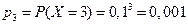 , (
, (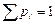 – проверка).
– проверка).





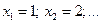 Пусть событие А появилось в k – ом испытании, то в предшествующих k – 1 испытаниях оно не появлялось. Вероятность этого события найдем по теореме умножения:
Пусть событие А появилось в k – ом испытании, то в предшествующих k – 1 испытаниях оно не появлялось. Вероятность этого события найдем по теореме умножения: 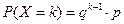 , где q =1– p – вероятность не появления события А. Полагая k = 1, 2, 3, …, получим геометрическую прогрессию с первым членом р и знаменателем q. По этой причине распределение называют геометрическим. Запишем в виде таблицы.
, где q =1– p – вероятность не появления события А. Полагая k = 1, 2, 3, …, получим геометрическую прогрессию с первым членом р и знаменателем q. По этой причине распределение называют геометрическим. Запишем в виде таблицы.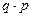
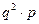
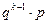
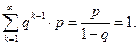
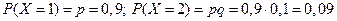 и т.д. Получаем:
и т.д. Получаем: