
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоремы умножения вероятностейСодержание книги
Поиск на нашем сайте
Произведением (или пересечением) событий А и В называется событие С, состоящее в осуществлении и события А, и события В, т.е. С = А . В. Вероятность события А, найденная в предположении, что событие В наступило, называется условной вероятностью события А относительно события В: P Пример. В урне 4 белых и 3 черных шара. Вынимают последовательно 2 шара. Найти вероятность того, что 2 шар черный, при условии, что 1 шар черный. Событие А – 1 шар черный, событие В – 2 шар черный. P Если произошло А, то осталось 6 шаров (4+2), Теорема. Вероятность произведения событий А и В равна произведению вероятности одного из них на условную вероятность другого относительно первого: Доказательство. Пусть из общего числа n случаев событию А благоприятствуют m случаев, k случаев благоприятствуют событию В. Пусть l случаев благоприятствует и событию А и событию В. Тогда Пример. Среди 25 лампочек 4 нестандартные. Найти вероятность того, что 2 взятые одновременно лампочки окажутся нестандартными. Событие А – первая лампочка нестандартная, событие В – вторая лампочка нестандартная. P(A) =
События А и В называются независимыми, если вероятность одного из них не изменяется при наступлении другого, т.е. P Теорема. Вероятность произведения двух независимых событий равно произведению их вероятностей Пример. Из двух орудий стреляют по цели. Вероятность попадания первого – 0,9, второго – 0,8. Из орудий делают одновременно по одному выстрелу. Найти вероятность того, что будет два попадания в цель. Событие А – первое попало, В – второе попало. Вероятность появления хотя бы одного события Пусть в результате испытания могут появиться n независимых событий, либо некоторые из них, либо ни одного события. Считаем вероятности появления каждого из событий Теорема. Вероятность появления хотя бы одного из независимых событий Пусть А – появление хотя бы одного из событий Следствие. Если события Пример. Вероятность попадания в мишень для трех стрелков 0,6; 0,7; 0,8 соответственно. Найти вероятность хот бы одного попадания при одном залпе. Пусть
Теорема сложения вероятностей Суммой или объединением А и В называется событие С, состоящее в наступлении события А, или события В или событий А и В вместе: С = А + В. Теорема. Вероятность суммы конечного числа несовместных событий равна сумме их вероятностей. Докажем для двух событий. Пусть из общего числа n случаев событию А благоприятствует k случаев, а событию В – l случаев. Тогда По условию, события А и В несовместимы. Следовательно, ни один из k случаев, благоприятствующих А, не благоприятствует В. Сумме А + В благоприятствует k + l случаев из n, поэтому Теорема. Вероятность суммы совместных событий равна сумме вероятностей этих событий без вероятности их произведения: Для доказательства следует рассмотреть диаграмму Виена. Следствие 1. Сумма вероятностей событий, образующих полную группу, равна 1. Событие 2. Сумма вероятностей противоположных событий равна 1, т.е.
Формула полной вероятности
Пусть событие А может произойти в результате появления одного и только одного события Н Теорема. Вероятность события А, которое может наступить при появлении одной из гипотез Н Доказательство. Событие А равносильно тому, что произойдет А и Н
Пример. На конвейер поступает продукция трех станков (50% – I, 30% – II, 20% – III). Брак составляет для первого станка 2%, для 2го – 3%, для 3го – 5%. Найти вероятность того, что случайно взятая деталь будет доброкачественной. Событие А – деталь доброкачественная. Возможны гипотезы: Н По формуле полной вероятности: 21.9. Формула Байеса (Бейеса)
Пусть имеется полная группа несовместных гипотез Н По теореме умножения вероятностей:
Пример. Вероятность поражения цели при одном выстреле для первого орудия – 0,2, для второго – 0,1. Каждое орудие произвело по одному выстрелу, одно попало в цель. Какова вероятность, что удачный выстрел совершило первое орудие? Событие А – попадание в цель. Гипотеза Н
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 245; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.68.161 (0.006 с.) |

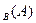 .
. (B) -?
(B) -?

 , а условная вероятность события В относительно события А есть Р
, а условная вероятность события В относительно события А есть Р 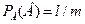 ,т.к. вместо n случаев остается возможным m случаев (событие А произошло). Тогда
,т.к. вместо n случаев остается возможным m случаев (событие А произошло). Тогда 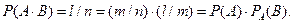
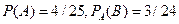 . Тогда
. Тогда 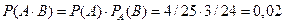 .
.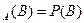 . Иначе – зависимые события.
. Иначе – зависимые события.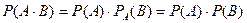 .
.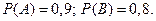 События A и B независимые, поэтому
События A и B независимые, поэтому 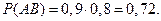
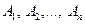 известными и равными
известными и равными  . Тогда вероятности противоположных событий
. Тогда вероятности противоположных событий 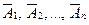 обозначим
обозначим 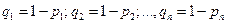 . Появление хотя бы одного события – это появление одного, двух,.., n событий.
. Появление хотя бы одного события – это появление одного, двух,.., n событий.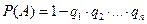 .
.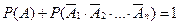 . По теореме умножения
. По теореме умножения 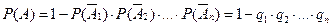 .
.
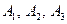 – попал в мишень первый, второй и третий стрелок. Событие А – хотя бы одно попадание в мишень. Тогда
– попал в мишень первый, второй и третий стрелок. Событие А – хотя бы одно попадание в мишень. Тогда 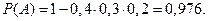
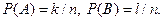
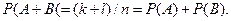 Методом математической индукции теорему можно обобщить на произвольное число несовместных событий.
Методом математической индукции теорему можно обобщить на произвольное число несовместных событий.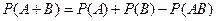 .
.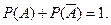
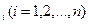 из некоторой полной группы несовместных событий (полная система). Н
из некоторой полной группы несовместных событий (полная система). Н 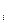
 обычно называют гипотезами.
обычно называют гипотезами. .
.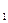 , либо А и Н
, либо А и Н 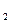 , либо А и Н
, либо А и Н 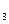 ,…, либо А и Н
,…, либо А и Н 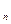 . Тогда по теоремам сложения (несовместных событий) и умножения
. Тогда по теоремам сложения (несовместных событий) и умножения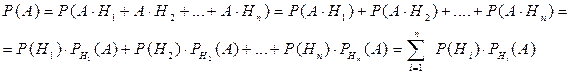
 – вероятность взять доброкачественное изделие, изготовленное 1м станком: P
– вероятность взять доброкачественное изделие, изготовленное 1м станком: P 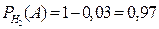 , P
, P 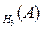 = 1–0,05 = 0,95. Вероятности гипотез даны по условию: P (H
= 1–0,05 = 0,95. Вероятности гипотез даны по условию: P (H  , P (H
, P (H 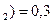 , P (H
, P (H 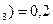 .
.

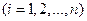 известны до опыта. Производится опыт, в результате которого зарегистрировано событие А. Известно, что этому событию наши гипотезы приписывали определенные вероятности P
известны до опыта. Производится опыт, в результате которого зарегистрировано событие А. Известно, что этому событию наши гипотезы приписывали определенные вероятности P 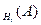
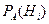 .
.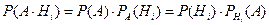 .
.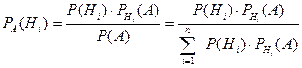 (i = 1,…, n). Это – формула Байеса, где
(i = 1,…, n). Это – формула Байеса, где 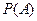 – вероятность появления события А.
– вероятность появления события А.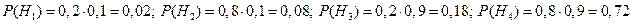 (
(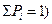 .
.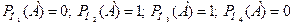 , т.е. гипотезы Н
, т.е. гипотезы Н 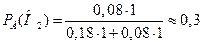 – вероятность того, что попало второе орудие;
– вероятность того, что попало второе орудие; 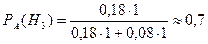 – вероятность того, что попало первое орудие.
– вероятность того, что попало первое орудие.


